|
Each Bookends puzzle is an esoteric string of 132 non-zero, decimal digits.
I create each Bookends puzzle in turn by methodically concatenating random permutations of pre-screened prime-numbers respectively 3-6 digits in length. The culls are the prime numbers with a 0 digit. Your goal is to recover the original substrings which I placed side by side. All 2-3 dozen of them! The rub is the inevitable presence of false positives. The trick is to not take the bait every time. Look ahead a prime number or two. You know, deductive reasoning. |
Here is another hint.
Prune the string outside-in. Left-to-right and right-to-left. Lop off the bookends, again and again. Do so until, ideally, there is nothing left of the original string.
A Bookends puzzle can be solitaire. A Bookends puzzle can be two-person, as well. In two-person chess, obviously, one player plays the white pieces while the other the black. In two-person Bookends, theoretically, one player lops off prime numbers left-to-right while the other does so right-to-left. |
|
Gurtle is not Wordle. Close but no cigar.
We need to have a level set before we can move on, just so we are on the same page. Like Wordle, Gurtle picks a one-word answer ... only to withhold it from you. Beyond that, Gurtle is not anything at all like Wordle. For starters, Gurtle converges on the correct answer. Wordle would risk going on and on indefinitely if it did not set an arbitrary limit on the number of chances to guess again. At a deeper plane of conceptualization, the tempo of Gurtle is rapid-fire throughout. For instance, Gurtle picks not only the answer but the opening guess too! Wordle does not do that. Instead, playing Wordle, you come off as a deer caught in headlights. Wordle's notorious, pregnant pauses result from you self-consciously squirming anxious to not make a social blunder. I have been there. Automatically picking the opening guess, as well as the answer, immediately breaks the Gurtle ice. It frictionlessly gets you over the hump and right into the midst of the Gurtle puzzle. It relieves any pressure on you to make a sufficiently-sophisticated, opening guess.
I think you get this key distinction which I find myself belaboring. Every Gurtle guess is productive. It is impossible to waste a Gurtle guess, unlike Wordle. Thanks to Gurtle's built-in process-of-elimination, I have even solved Gurtle with a single follow-up guess that was so "wrong" that it autonomically precipitated an intrinsic phenomenon of inverse selection. Wordle is fixated on the same, lame 2309 five-letter words. Gurtle can play those words, or an expanded set of five-letter words, or anywhere from six-letter words to twelve. Beyond that, there simply are not enough words to make it worthwhile. Wordle is offered on a niggardly, one-puzzle-a-day basis, while Gurtle is an infinite loop of puzzles and is always available here and, moreover, exclusively here. Gurtle will "spin the wheel" and select a word length for you, unless you pick one yourself. Either way, Gurtle thereupon always selects a pair of words to begin each puzzle. The first word of each pair is ho-hum. It is what you have to correctly guess in order to solve the puzzle. The second word of each pair is something else. The second word is involuntarily employed as your first guess. Tough cookies! You are stuck with it whether you approve of it or not. The second word, by the way, is a complimentary guess, meaning it is not counted against you. The second word is also an automatic guess, meaning say good-bye to your usual first-guess-case of jitters - inasmuch as you join each Gurtle puzzle in progress! Gurtle is an infinite loop of word puzzles. Hallelujah! Praise the Lord! You can try to solve them in turn as quickly as possible. Or you can take your sweet time about it! Gurtle is addictive in a good way. You encounter words that you never even imagined existed. I am Francis Gurtowski. You can thank me - for developing Gurtle and then making Gurtle freely available to you - by purchasing copies of my books. Some of my books are described below - the mere tip of my proverbial iceberg. All of my books - thousands of them, in fact - are listed at www.amazon.com\books. |
By Francis Gurtowski
The prolific author is an authentic, ancient coder,
going all the way back to IBM Poughkeepsie (Building 705, no less, second floor)
and the heyday of OS/360,
Robert Rex Seeber Jr. and the horizontal-microcoded System/360 Model 50,
coding pads and the coding-pad veto,
punch cards and keypunch machines,
and self-modifying code.
Francis Gurtowski is also a self-styled Henry Ford of contemporary, print-on-demand, book publishing.
Henry Ford is synonymous with the assembly line,
a perfected process for swiftly turning out
a series of ingenious, finished products
in a foolproof, mechanically-efficient manner.
Enter the JavaScript Code-Stylist
The computer ignores so-called "white space" except as the blanks, tabs, newlines, formfeeds, and comments separate tokens.
As a consequence, only the rare coders
- in fact, maybe only the elusive "code poets" -
are fastidious about how they are visually presenting in their code.
The rub is that the worst torture
- akin to water-boarding -
anyone can inflict upon a coder is making him or her review another coder's code.
Such as during the the "code walk-throughs" which are part and parcel of the software development process performed at industrial scale.
The catch is that the code-reviewer is obligated to critically LOOK at the other coder's code for actionable flaws
but the code-reviewer is not permitted to CRITIQUE the other coder's code so as to otherwise improve it,
no matter how aesthetically barbaric the code-reviewer views it.
Do novelists have the same compulsion to rewrite every other novelist's story arcs and prose?
Enter the so-called "code stylist"
- akin to the "food stylist" -
whose calling is to make a dish look irresistably good enough to eat
for the camera.
Code reviews are arguably more effective after a code stylist has dressed up the code and maybe even colorized it.
C and Java are encrypted into 1's and 0's but Javascript abounds in clear text.
Maybe not so much anymore, but way back in 2016 that was true to a certain extent.
Using what is available, Francis Gurtowski tries his hand at code rendering.
He offers sample source code and a corresponding keyword cross reference in separate volumes.
He also offers both either colorized or not.

|
|

|
|||

|

|
||||

|

|

| |||
2,349,648 Quintessential Puzzles by Francis Gurtowski
|
This is yet another serious, serious series of books created by Francis Gurtowski.
The prolific author is an authentic, ancient coder, going all the way back to IBM Poughkeepsie (Building 705, no less, second floor) and the heyday of OS/360, Robert Rex Seeber Jr. and the horizontal-microcoded System/360 Model 50, coding pads and the coding-pad veto, punch cards and keypunch machines, and self-modifying code. Francis Gurtowski is also a self-styled Henry Ford of contemporary, do-it-yourself, print-on-demand, book publishing. Henry Ford is synonymous with the assembly line, a perfected process for swiftly turning out a series of ingenious, finished products in a foolproof, mechanically-efficient manner. All 999 of these sequels take full advantage of (Amazon) Kindle Direct Publishing's twin, generous, upper limits of 590 bound-and-paperbacked, 8.5x11-inch pages. |
This substantial series of weighty books - by Francis Gurtowski and collectively titled Quintessential Puzzles - is true to its quotidian name.
The 2,352 separate and distinct brain-teasers forming each volume - and the total of 2,349,648 specimens of this riddle subspecies which have been collected for your enjoyment and vocabulary development within the entire 999-book Quintessential Puzzles assemblage - are perfect examples of no-frills word-puzzles. As the fictional Los Angeles police sergeant Friday would say on the classic 1950s whodunit television series Dragnet, "Just the words, ma'am." A solution to a Quintessential Puzzle is an ordered list of typically ten, eleven, twelve, or thirteen words satisfying certain criteria regarding each individual word's length and letter palette. Here is an outlying example of a Quintessential Puzzle whose ordered list of six words is much shorter than is usually the case. The gist of this exception will suffice to demonstrate the anatomy of a Quintessential Puzzle regardless of the number of words involved. |
The first word on this prototypical list happens to be specified to be precisely ten letters in length and spelled with at least one instance of each of these eight letters: DEGLORTY - and with absolutely no other letter or combination of letters.
A word such as TROGLODYTE, for example; there may or may not be more than one word that fits the profile. The second word on this list happens to be specified to be precisely eleven letters in length and spelled with at least one instance of each of these seven letters: AINQSUV - and with zero, one, or more of the letters of the palette prescribed for the first word: DEGLORTY - and with absolutely no other letter or combination of letters. A word such as EQUIVALENTS, for example. The third word on this list happens to be specified to be precisely eight letters in length and spelled with at least one instance of each of these three letters: FWZ - and with zero, one, or more of the cumulative letter-palette prescribed for the first two words: ADEGILNOQRSTUVY - and with absolutely no other letter or combination of letters. A word such as FROWZIER. |
The fourth word on this list happens to be specified to be precisely nine letters in length and spelled with at least one instance of each of these three letters: MPX - and with zero, one, or more of the cumulative letter-palette prescribed for the first three words: ADEFGILNOQRSTUVWYZ - and with absolutely no other letter or combination of letters.
A word such as EXAMPLING. The fifth word on this list happens to be specified to be precisely eight letters in length and spelled with at least one instance of each of these three letters: BCH - and with zero, one, or more of the cumulative letter-palette prescribed for the first four words: ADEFGILMNOPQRSTUVWXYZ - and with absolutely no other letter or combination of letters. A word such as BECHANCE. The sixth and final word on this unusual list is also specified to be precisely eight letters in length but spelled with at least one instance of each of these two letters: JK - and with zero, one, or more of the cumulative letter-palette prescribed for the first five words: ABCDEFGHILMNOPQRSTUVWXYZ. A word such as JOYSTICK. It does not get any simpler - nor any more difficult - than that. Each Quintessential Puzzle eventually - sooner or later - employs all twenty-six letters of the alphabet. In fact, it does not get any more quintessential than that. |

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
293,706 Pair-Off Puzzles by Francis Gurtowski
|
This is yet another serious, serious series of books created by Francis Gurtowski.
The prolific author is an authentic, ancient coder, going all the way back to IBM Poughkeepsie (Building 705, no less, second floor) and the heyday of OS/360, Robert Rex Seeber Jr. and the horizontal-microcoded System/360 Model 50, coding pads and the coding-pad veto, punch cards and keypunch machines, and self-modifying code. Francis Gurtowski is also a self-styled Henry Ford of contemporary, do-it-yourself, print-on-demand, book publishing. Henry Ford is synonymous with the assembly line, a perfected process for swiftly turning out a series of ingenious, finished products in a foolproof, mechanically-efficient manner. All 999 of these sequels take full advantage of (Amazon) Kindle Direct Publishing's twin, generous, upper limits of 590 bound-and-paperbacked, 8.5x11-inch pages. |
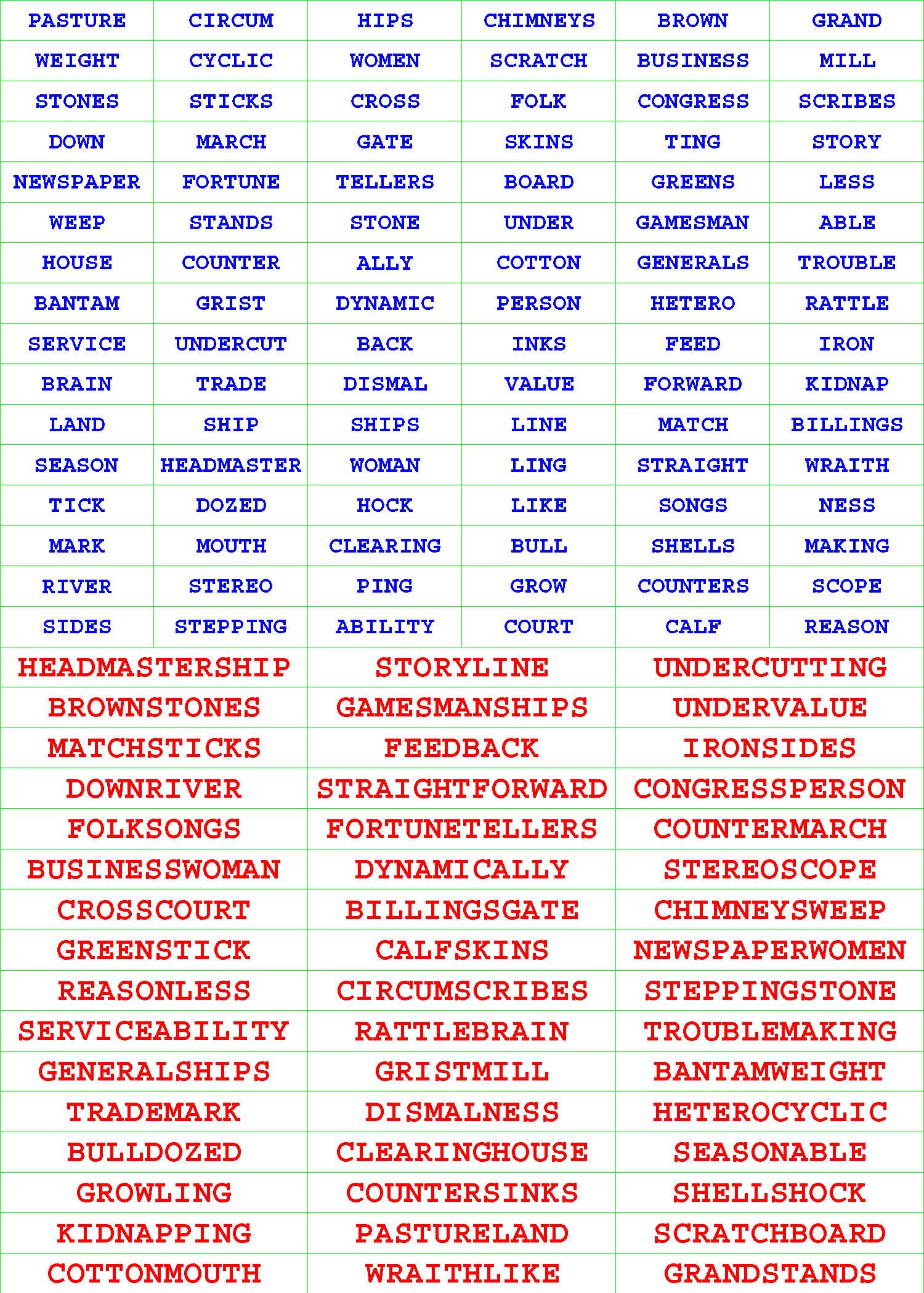
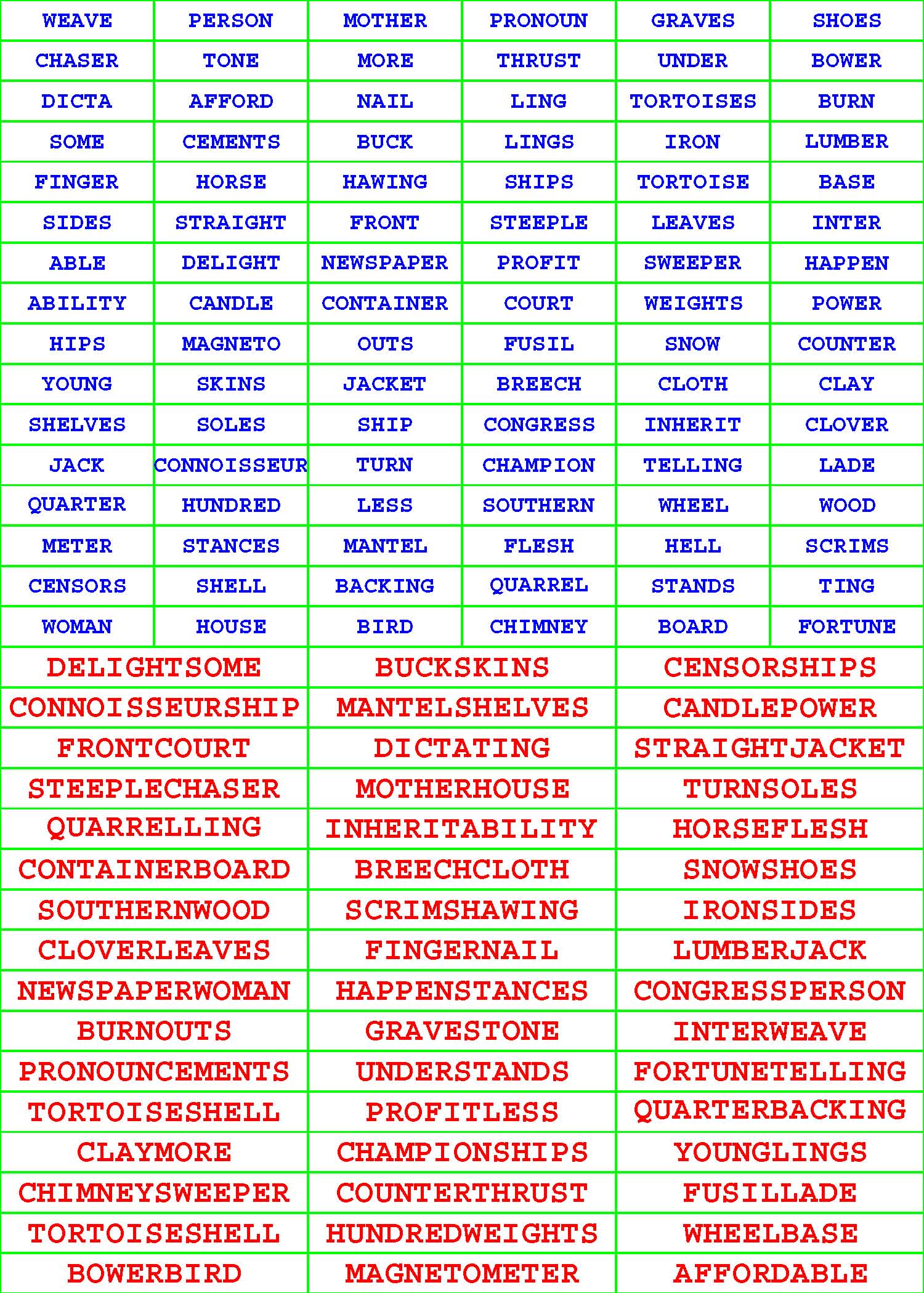
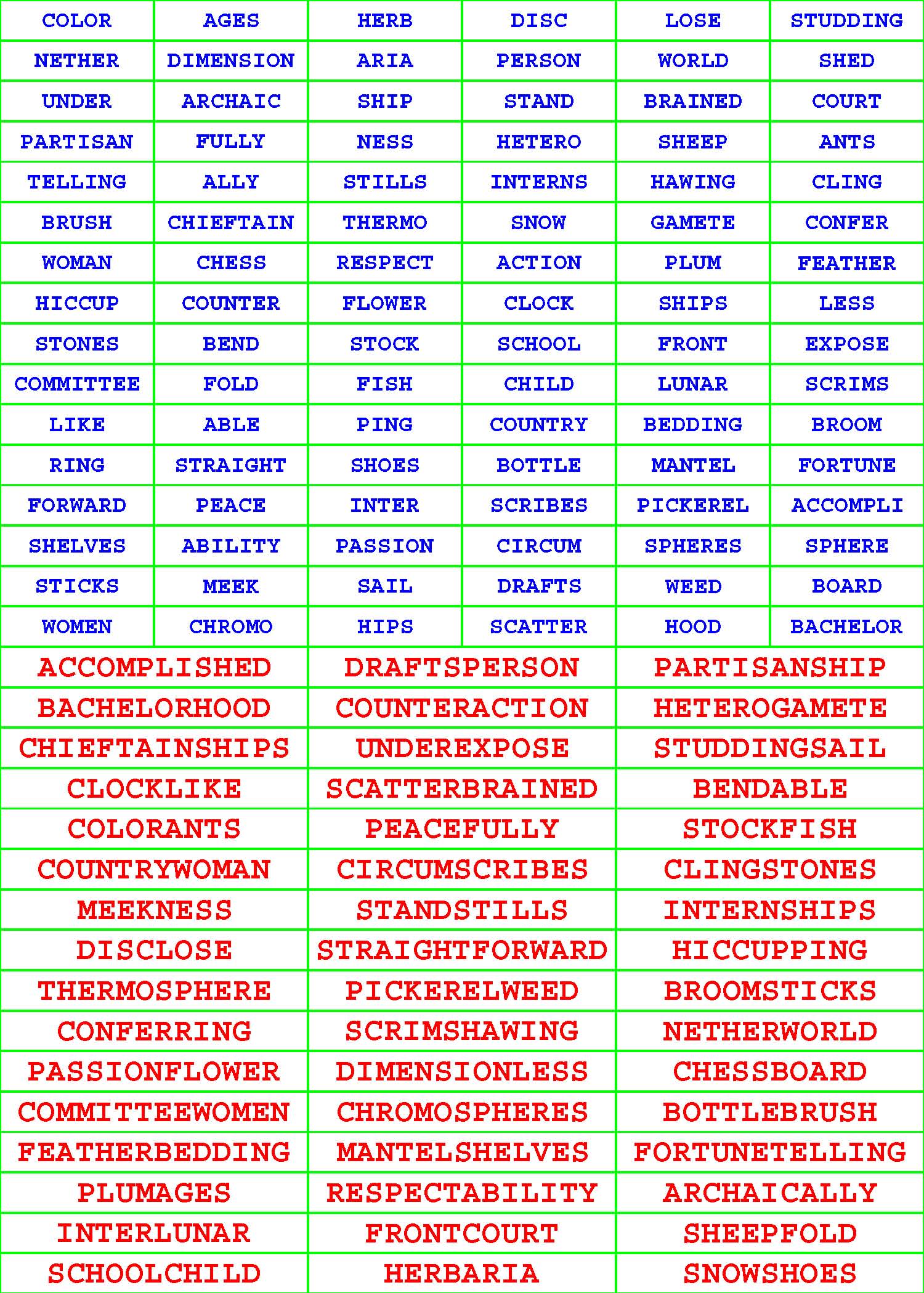
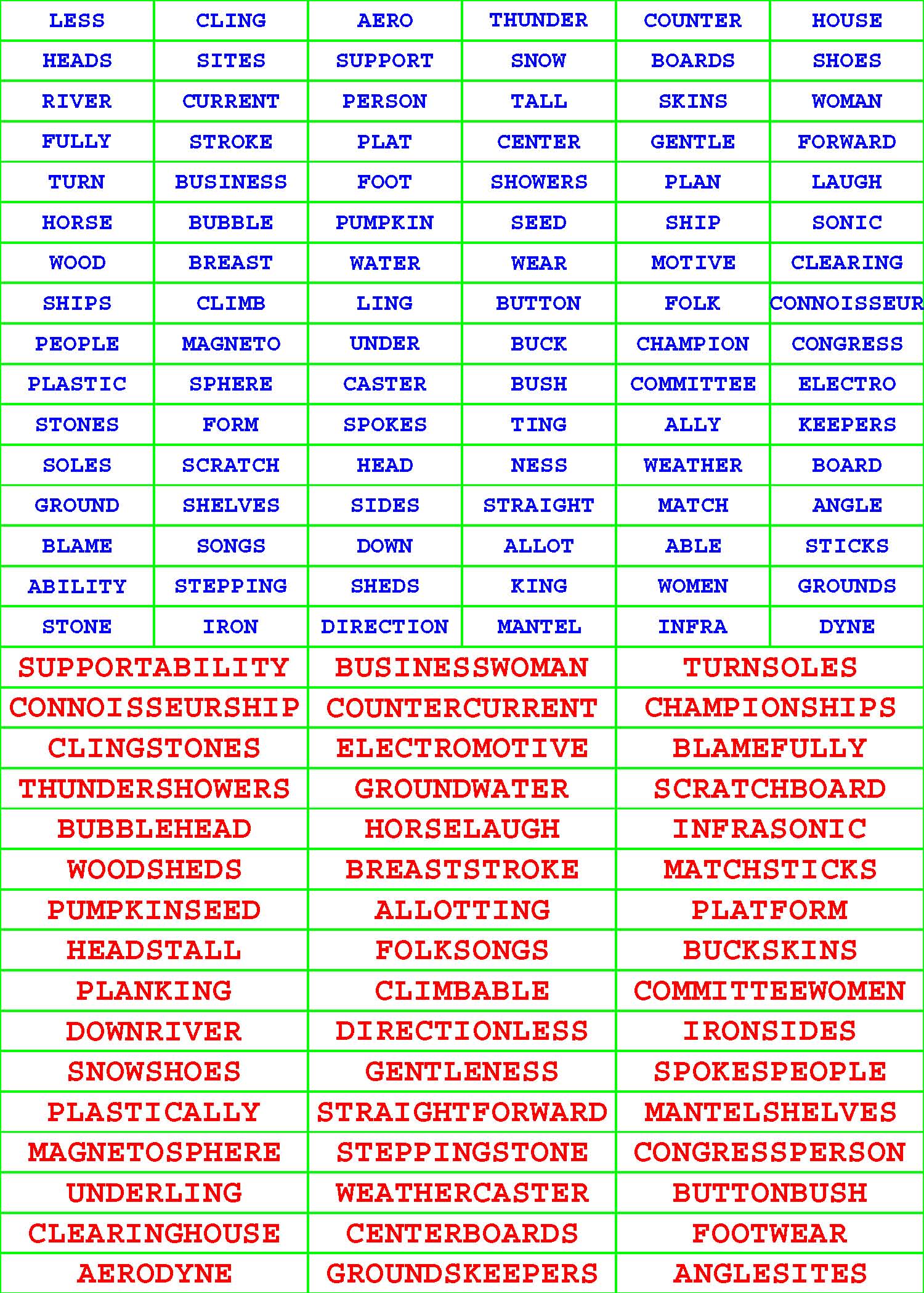
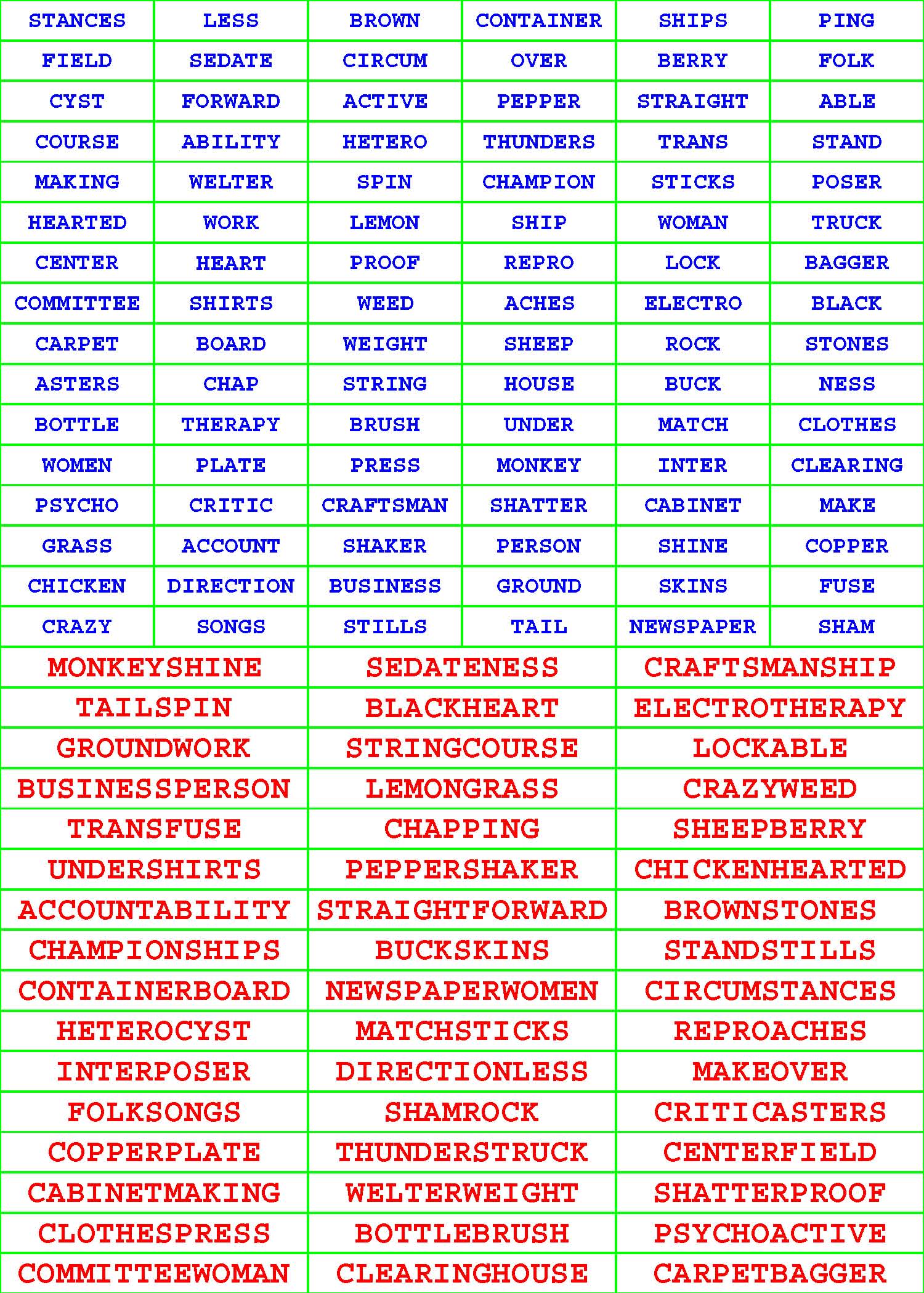
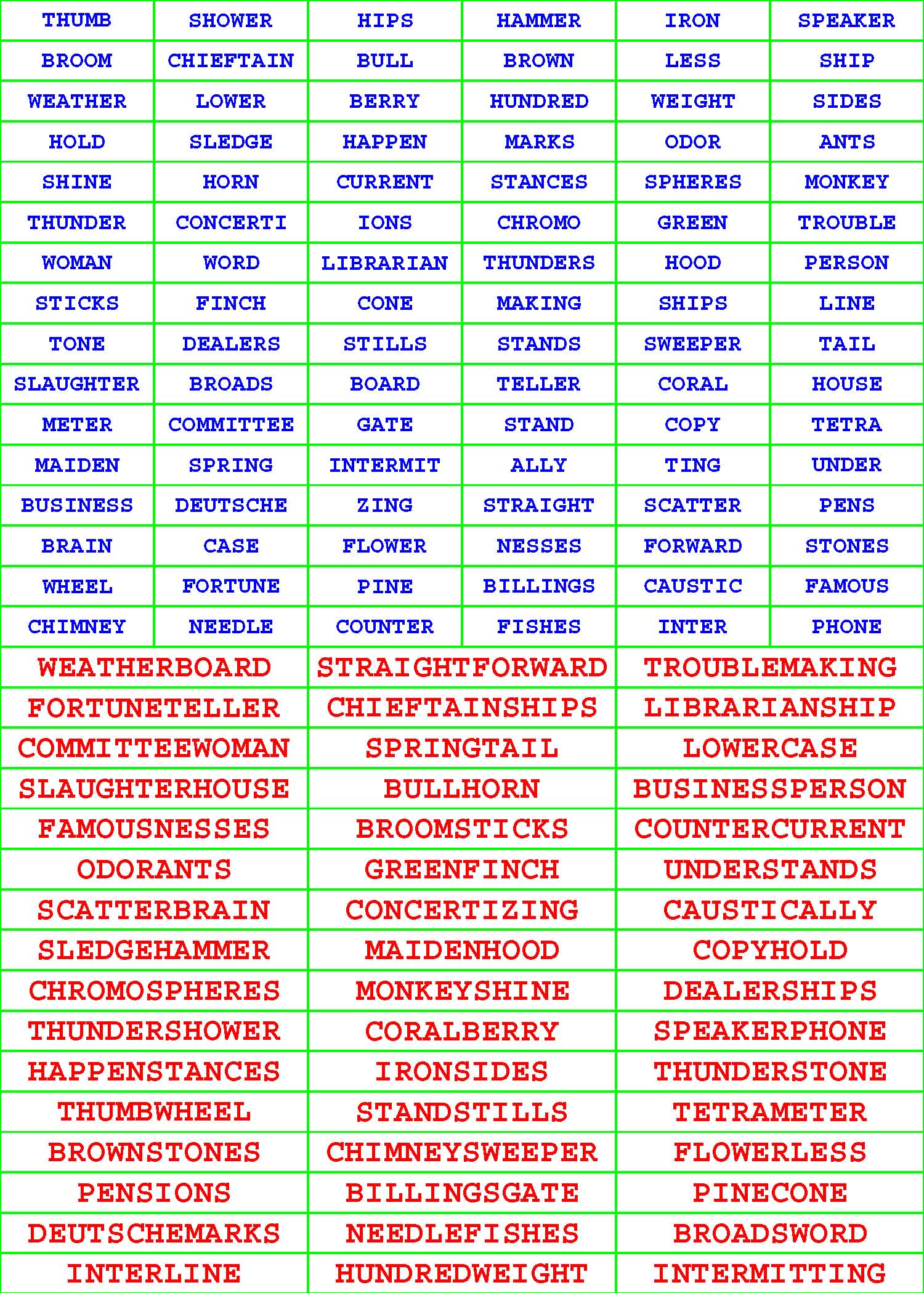
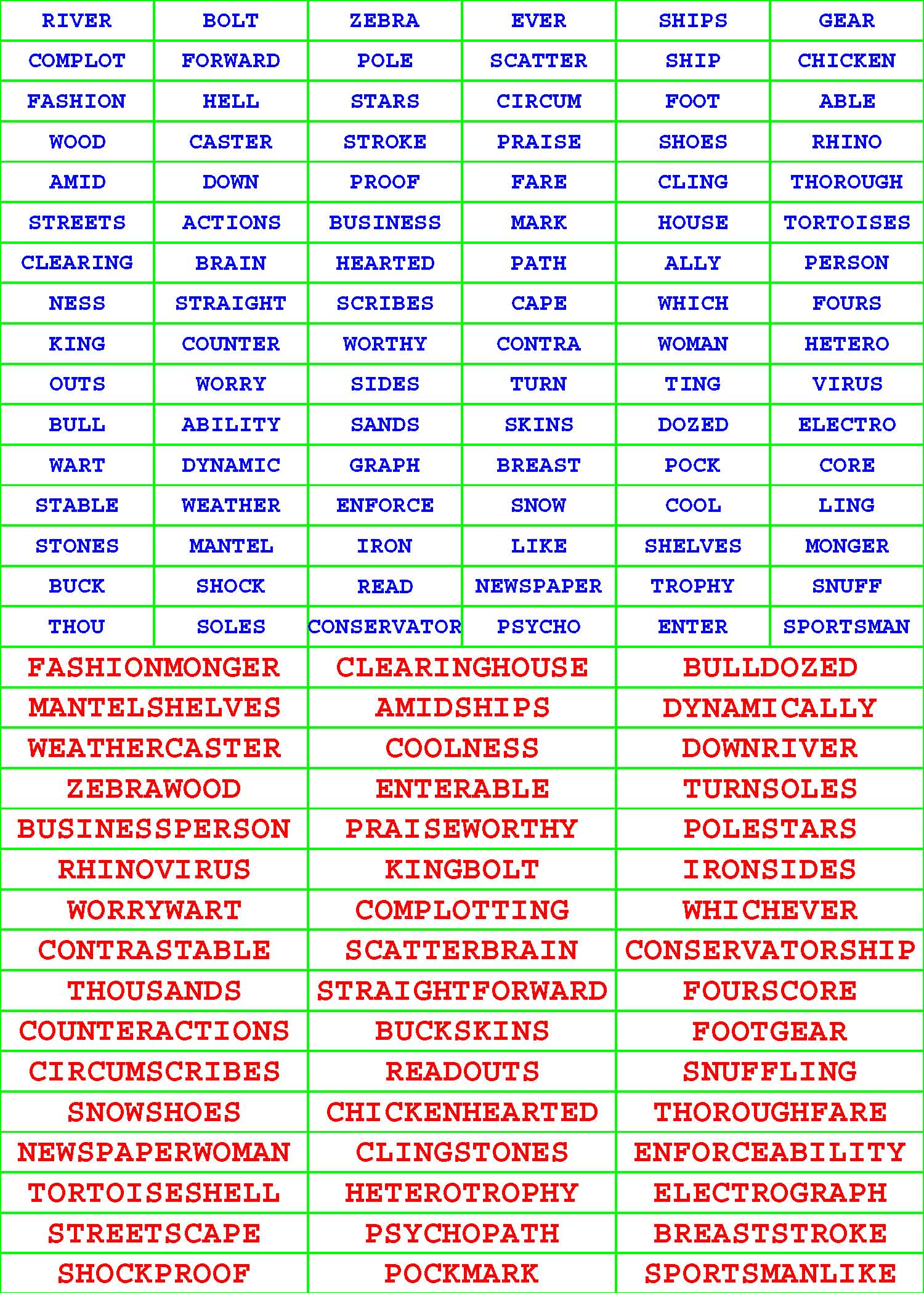
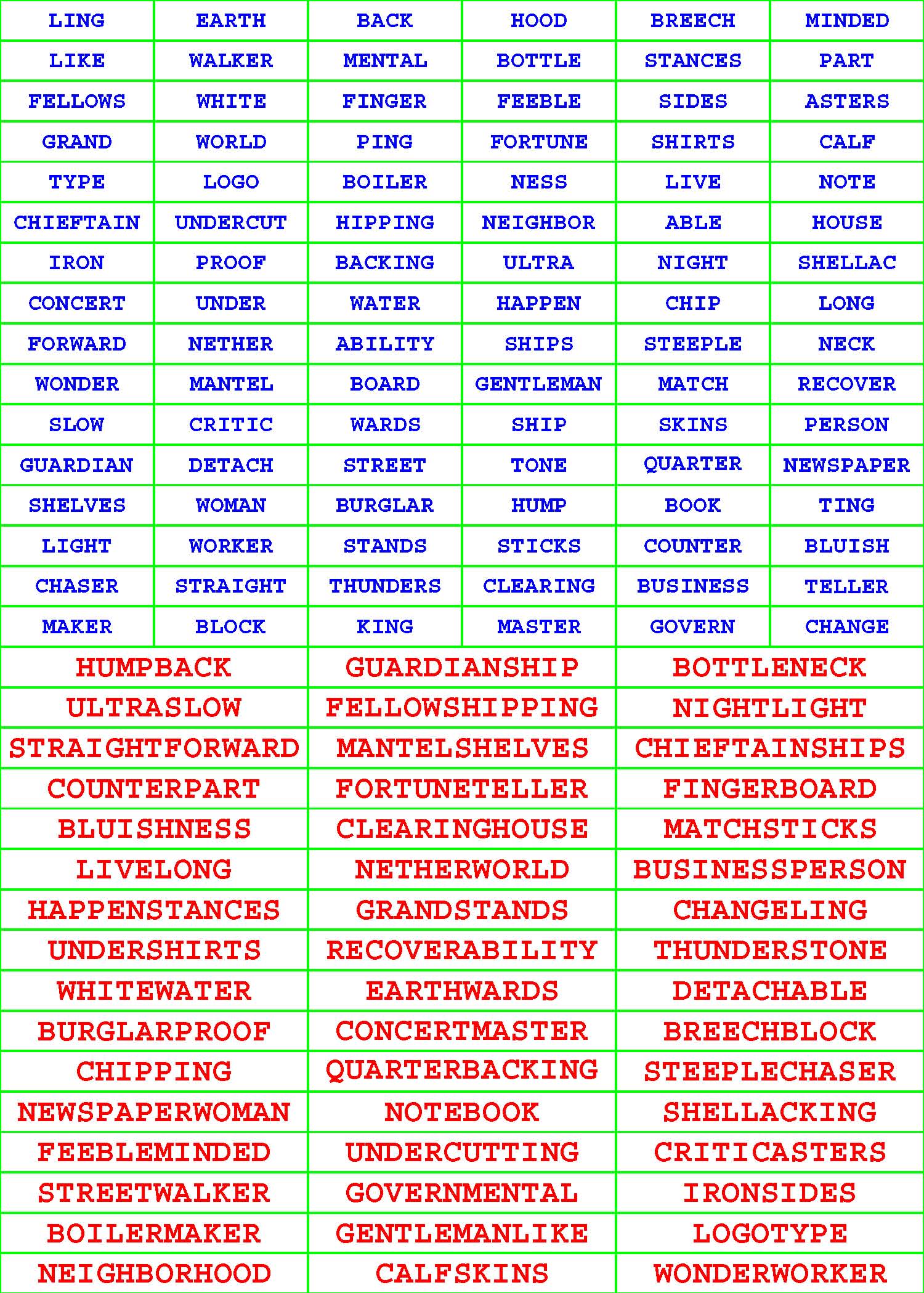
Each of the 294 given, riddled Pair-Off Puzzle grids in each book has sixteen rows and six columns and is populated with a different, diversified assortment of exactly ninety-six, dictionary words each from four to eleven letters long.
Each such given ninety-six-word aggregate has undergone a very, very, rigorous selection process. For starters, no two or more words within the confinement of any given subcollection are identical. More to the point, each given word within each grouping has a partner tucked away there on the sly. Unriddle each of the 294 given, riddled Pair-Off Puzzle grids by pairing off the ninety-six given words into forty-eight composite words of your own concoction. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Here Is Baby ... by Francis Gurtowski
|
This is yet another serious, serious series of books created by Francis Gurtowski.
The prolific author is an authentic, ancient coder, going all the way back to IBM Poughkeepsie (Building 705, no less, second floor) and the heyday of OS/360, Robert Rex Seeber Jr. and the horizontal-microcoded System/360 Model 50, coding pads and the coding-pad veto, punch cards and keypunch machines, and self-modifying code. Francis Gurtowski is also a self-styled Henry Ford of contemporary, do-it-yourself, print-on-demand, book publishing. Henry Ford is synonymous with the assembly line, a perfected process for swiftly turning out a series of ingenious, finished products in a foolproof, mechanically-efficient manner. |
Develop your precious young child's budding ability to pick out a familiar textual signal buried amid the studied ambient noise printed in various large Courier fonts on each line of this imposing, 590-page, pre-kindergarten - yea, pre-nursery school! - workbook.
Such alphabetic discernment is, of course, an essential language skill. Ask any schoolteacher. More to the point, arguably, the first letter sequence that every child ought to learn to pick out of a confusion of seemingly random letters is that of its own first name. Start right at the beginning by familiarizing your child with precisely that spelling. |
Consider this a treasure trove of letter problems to be solved directly on the pages of this workbook.
In the very beginning you, of course, will have to circle the letters with a pencil or crayon as your child points them out. Before this book is even halfway filled out, however, your confident child will no doubt insist on grabbing the proverbial reins out of your hands and marking-up the remaining pages unassisted. So be it. This snowballing procedure provides a written record of your child's progress in recognizing letter sequences. These pre-reading-skills exercises are structured into five progressive degrees of difficulty. |
Five 108-point Courier letters per line.
Then ten 54-point Courier letters per line. Then fifteen 36-point Courier letters per line. Then twenty 27-point Courier letters per line. Finally twenty-five 21.6-point Courier letters per line. By the time you and your child finish this massive tome your child will be well-prepared for kindergarten and beyond. And you will have a family heirloom to not only treasure yourself, but, someday in the not too distant future, to also show your child when your child moves into a college dormitory. |

|

|

|

|

|

|

|

|

|

|

|

|
Catchword Puzzles ... by Francis Gurtowski
|
This is yet another serious, serious series of books created by Francis Gurtowski.
The prolific author is an authentic, ancient coder, going all the way back to IBM Poughkeepsie (Building 705, no less, second floor) and the heyday of OS/360, Robert Rex Seeber Jr. and the horizontal-microcoded System/360 Model 50, coding pads and the coding-pad veto, punch cards and keypunch machines, and self-modifying code. Francis Gurtowski is also a self-styled Henry Ford of contemporary, do-it-yourself, print-on-demand, book publishing. Henry Ford is synonymous with the assembly line, a perfected process for swiftly turning out a series of ingenious, finished products in a foolproof, mechanically-efficient manner. All 999 of these sequels take full advantage of (Amazon) Kindle Direct Publishing's twin, generous, upper limits of 590 bound-and-paperbacked, 8.5x11-inch pages. |
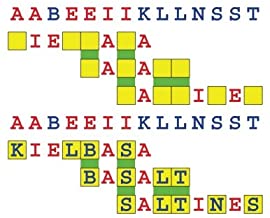
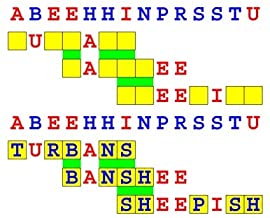
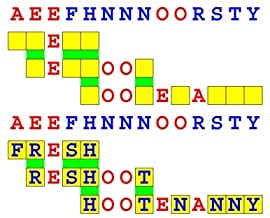
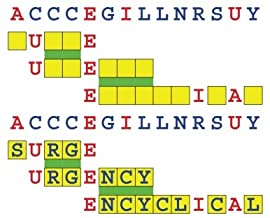
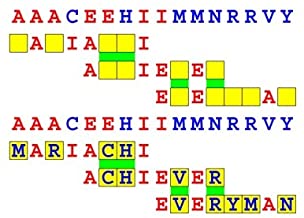
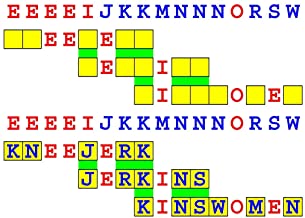
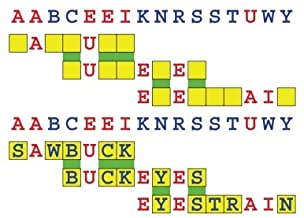
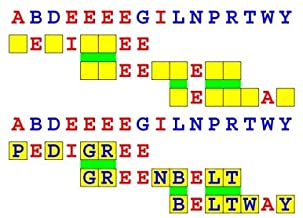
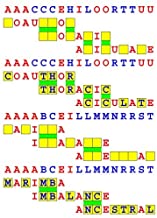
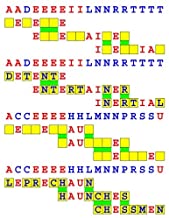
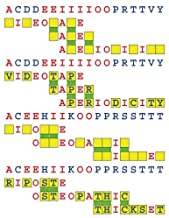
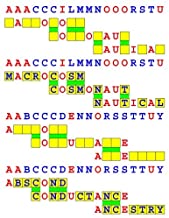
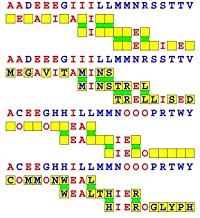
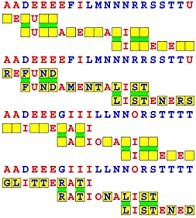
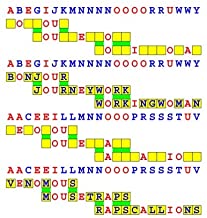
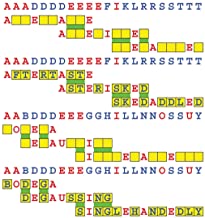
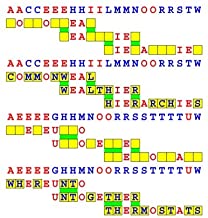
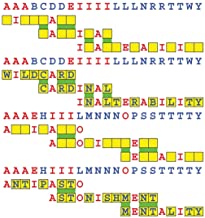
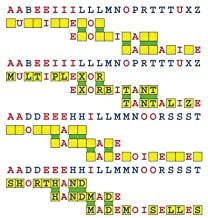
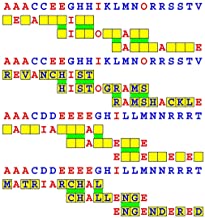
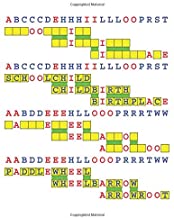
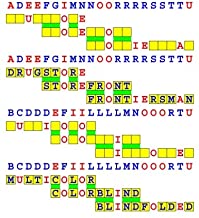
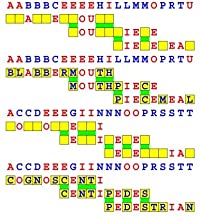
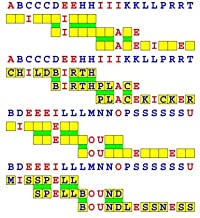
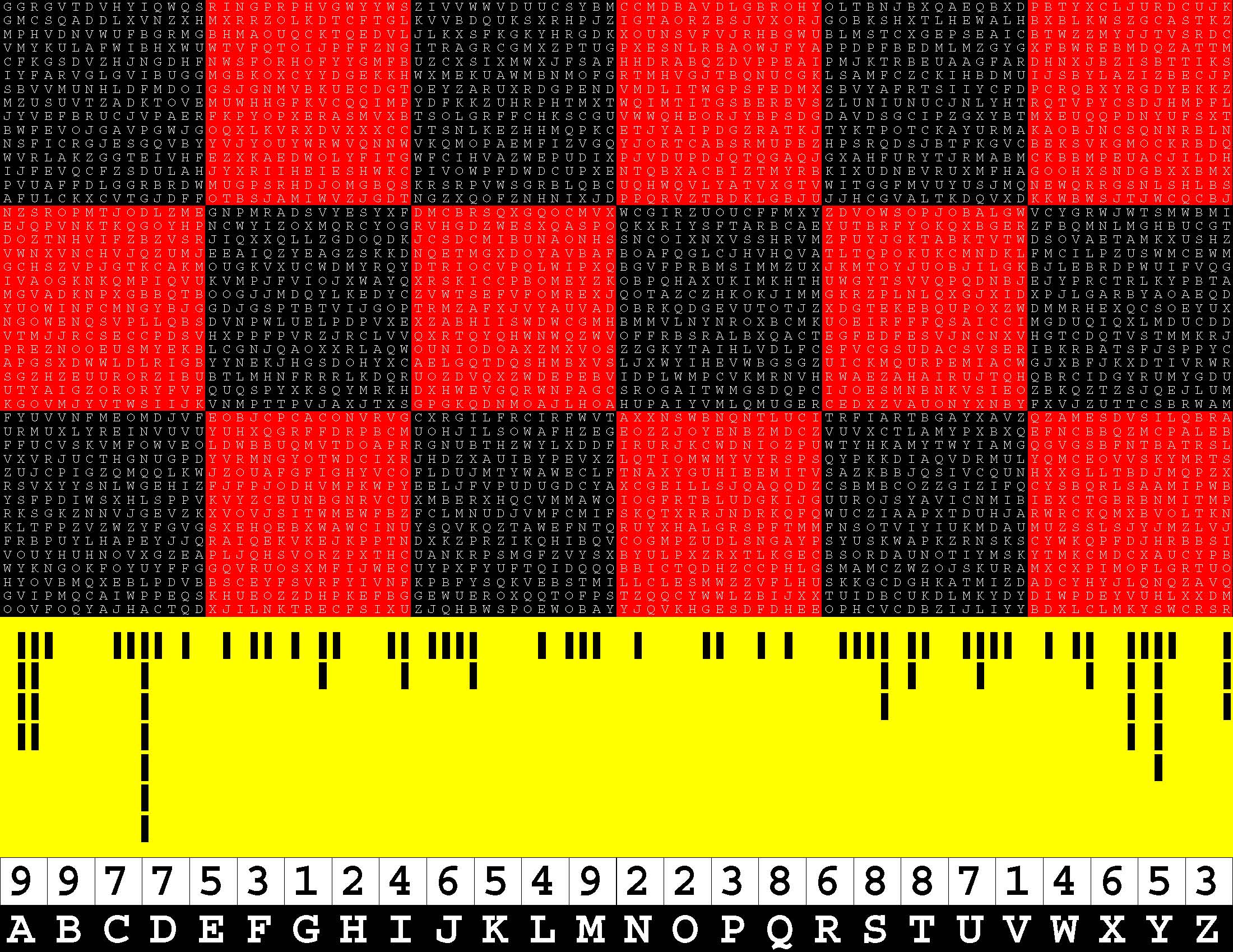
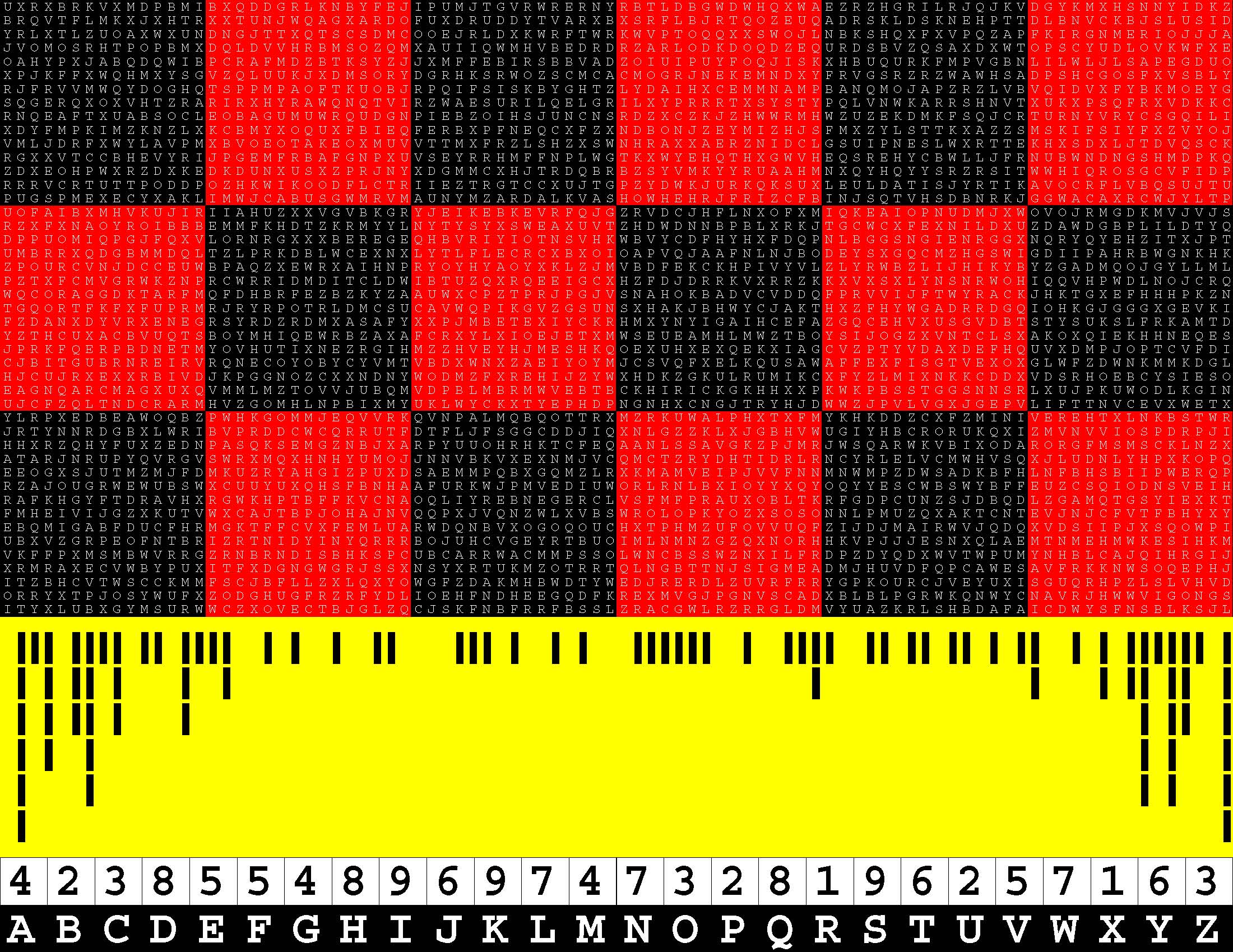
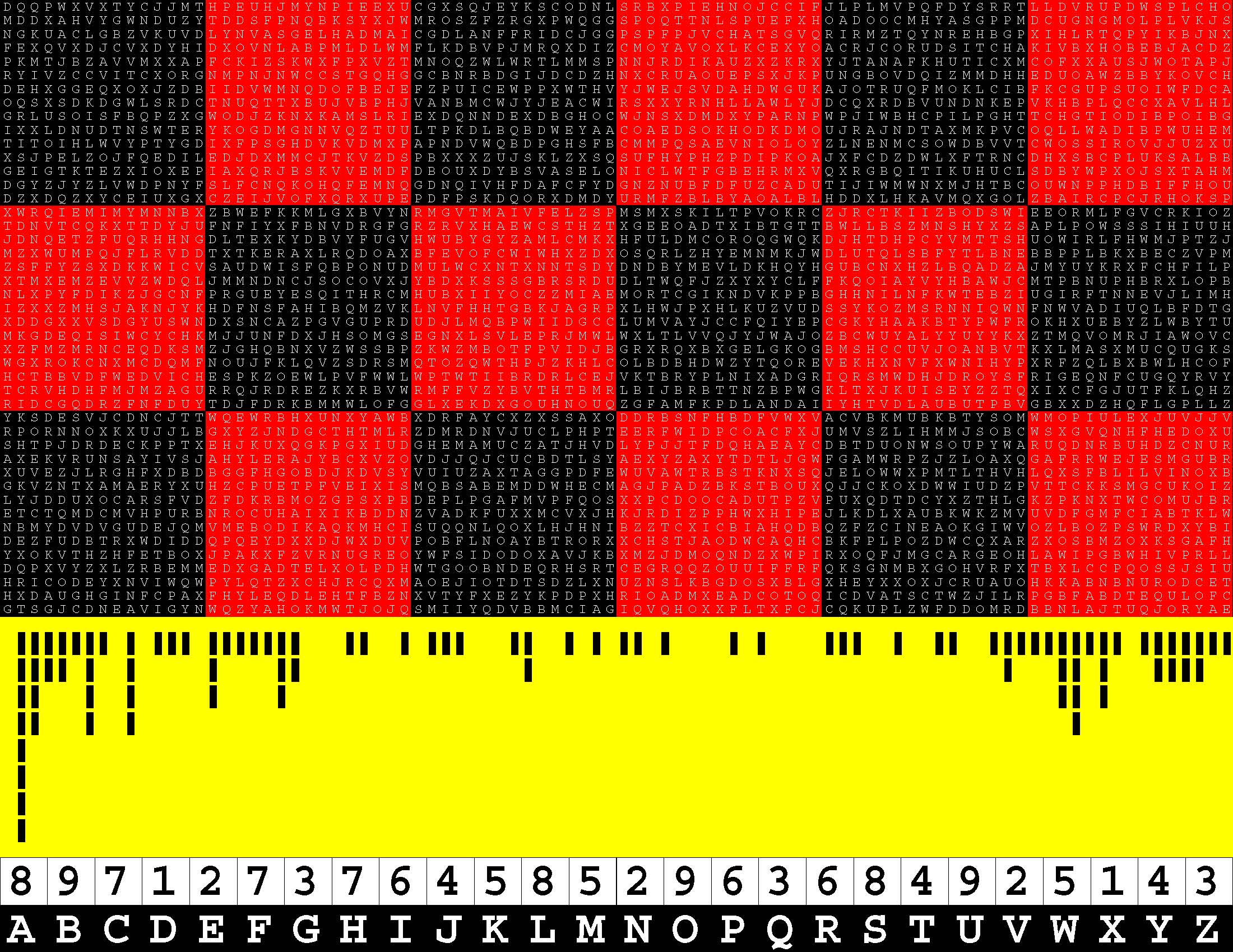
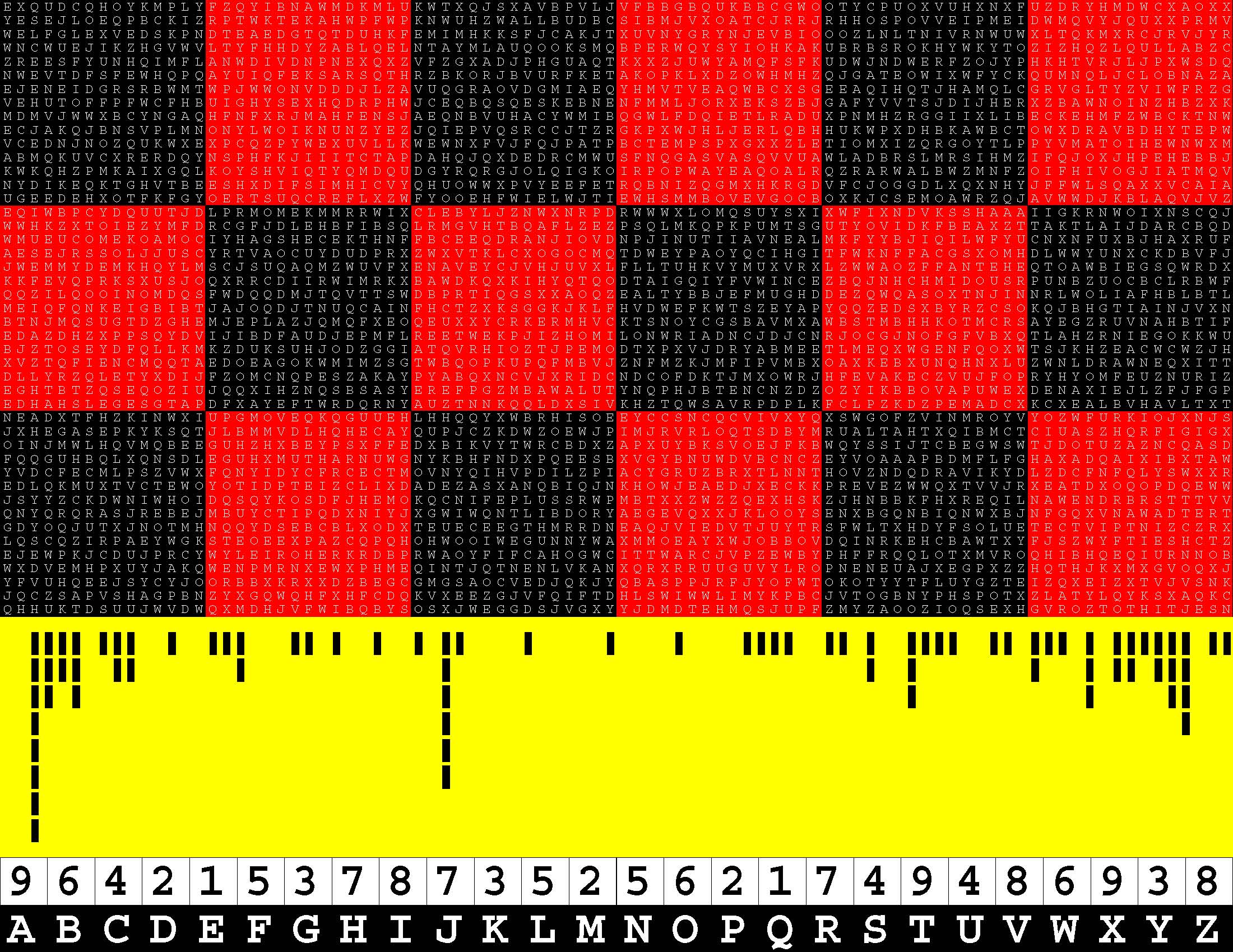
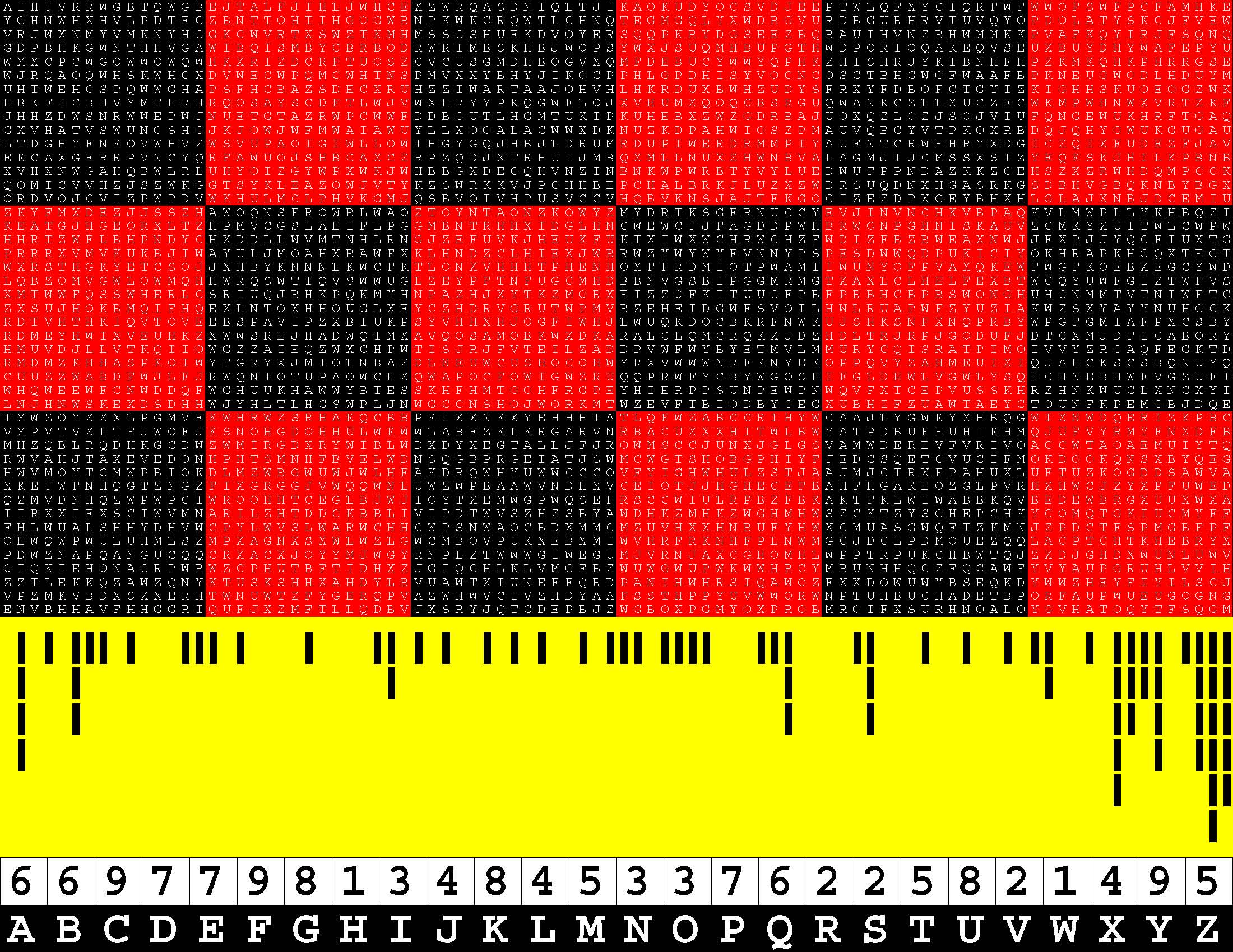
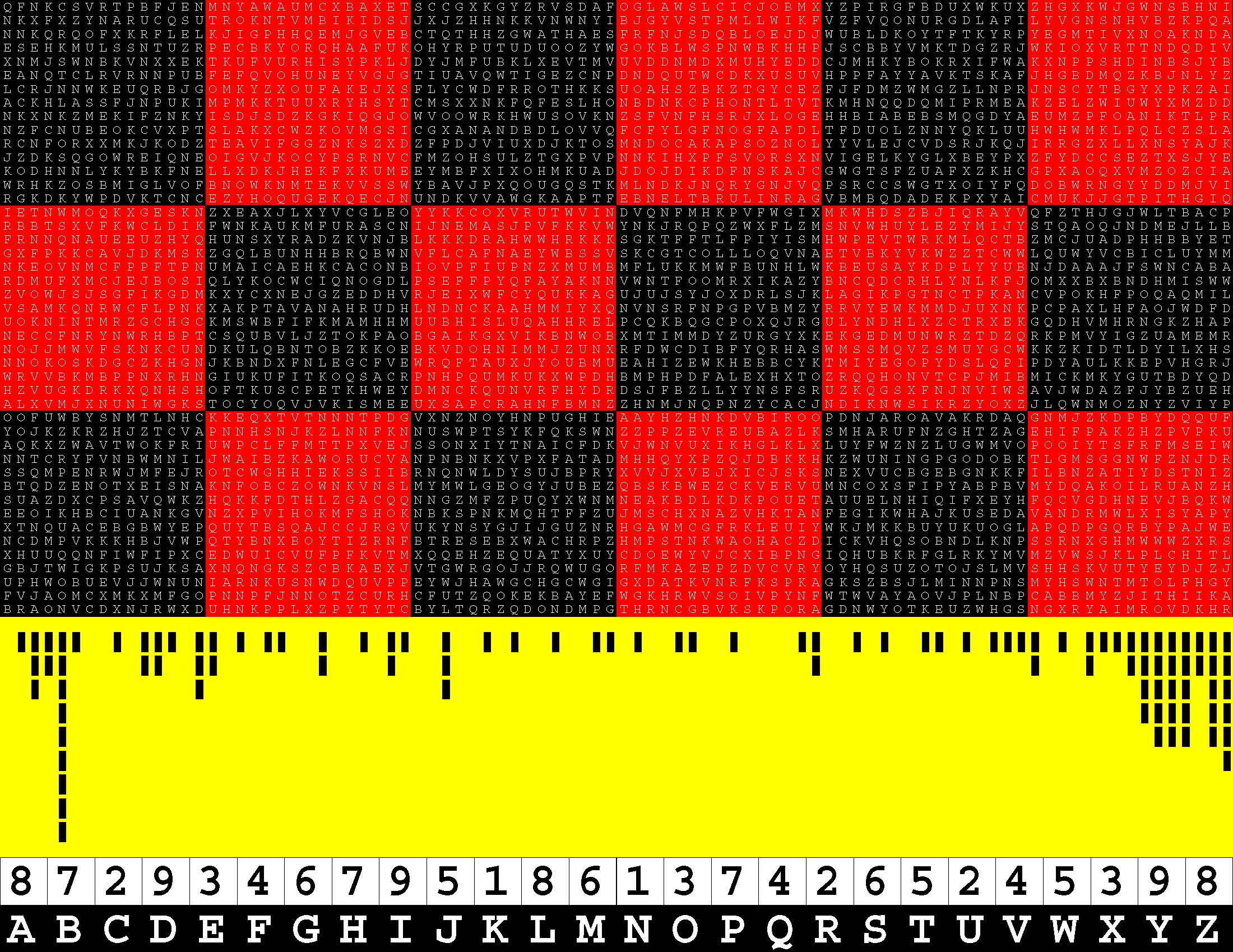
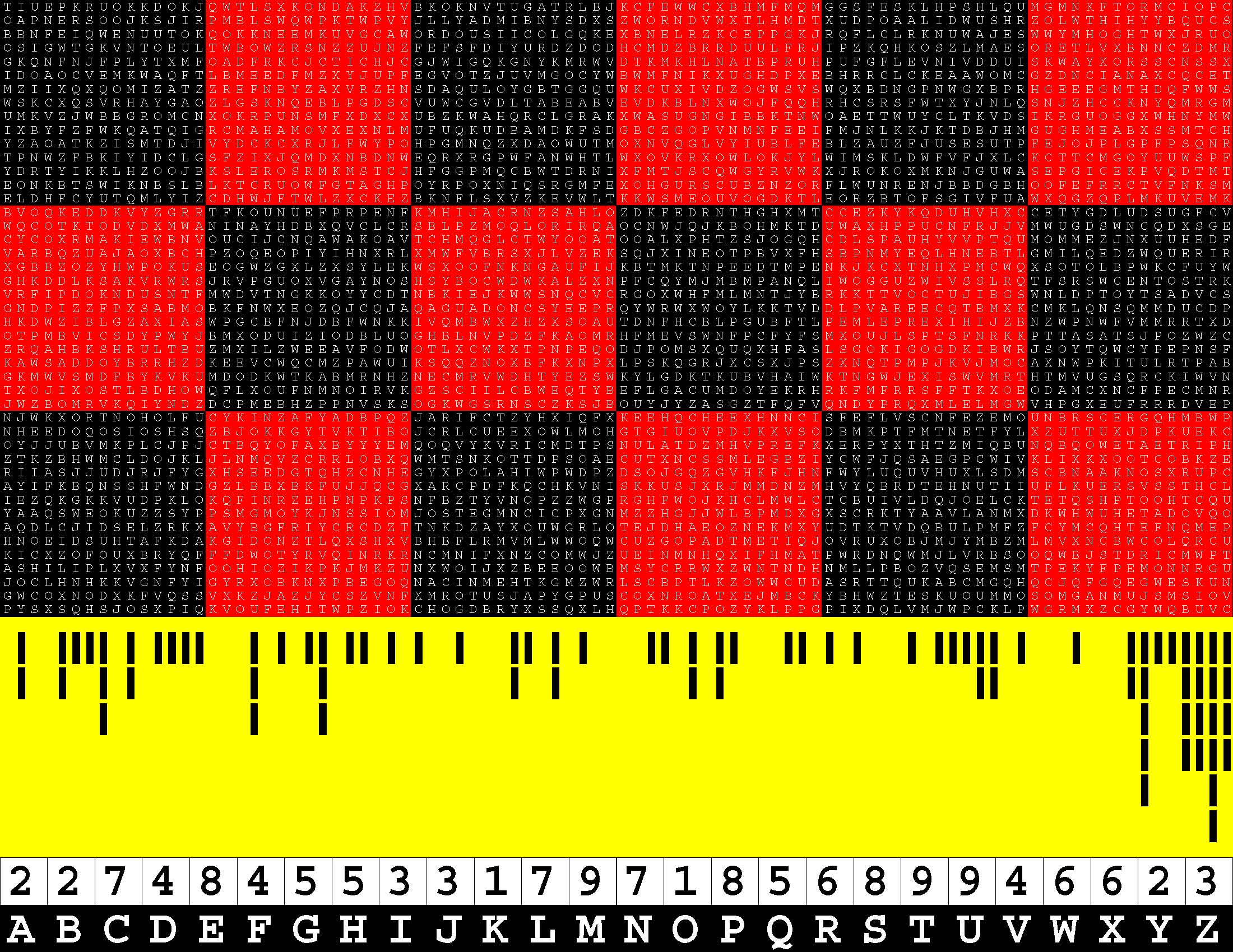
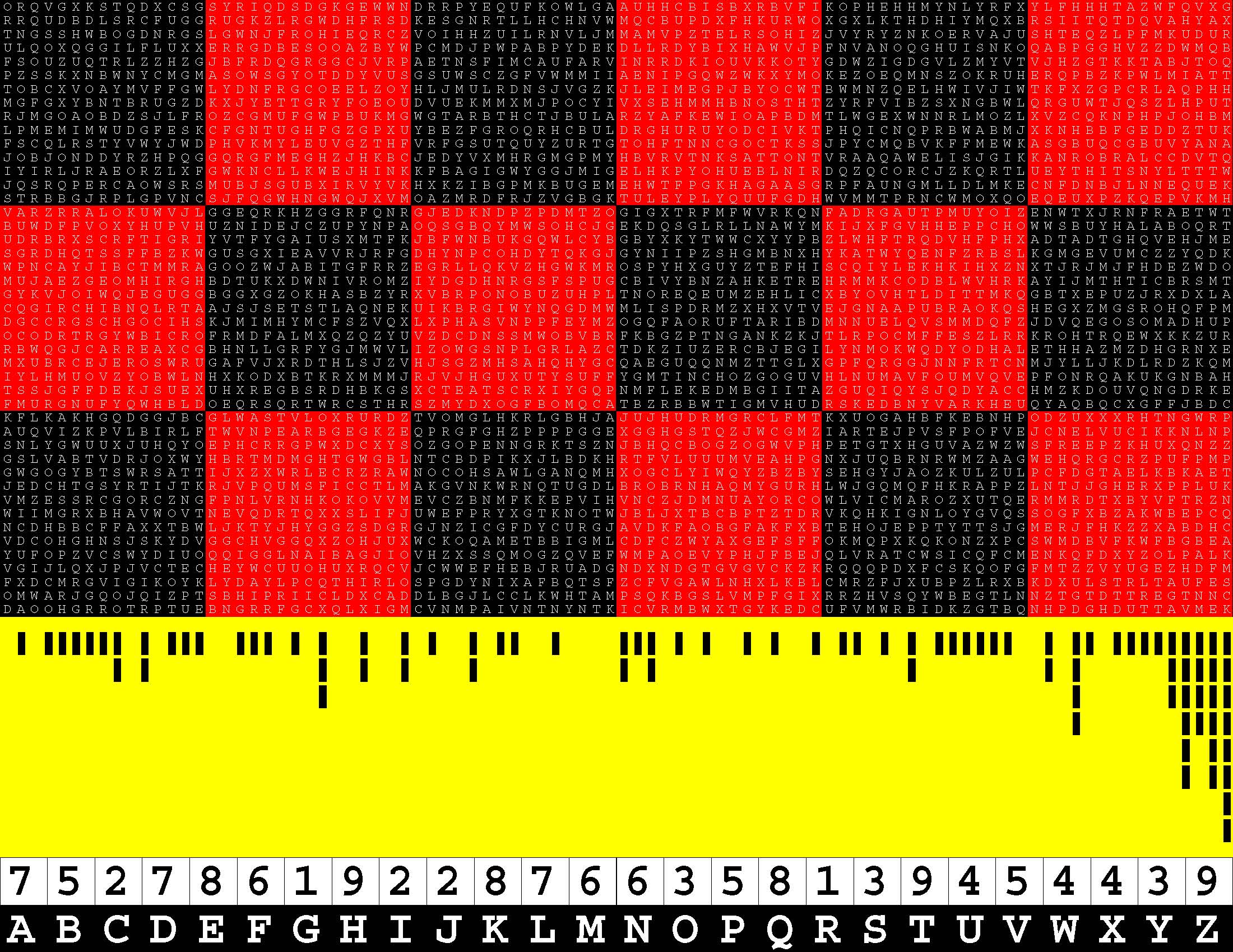
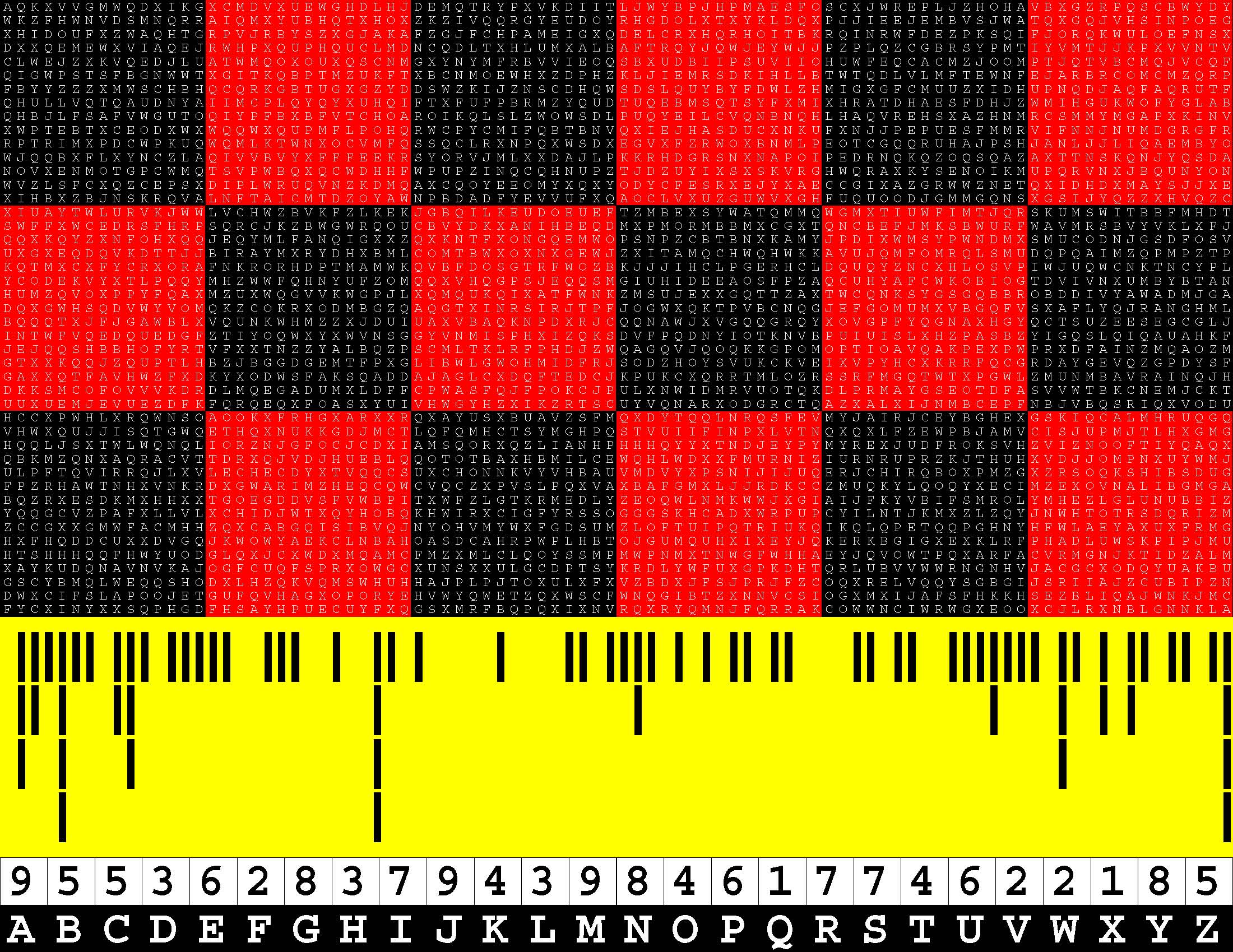
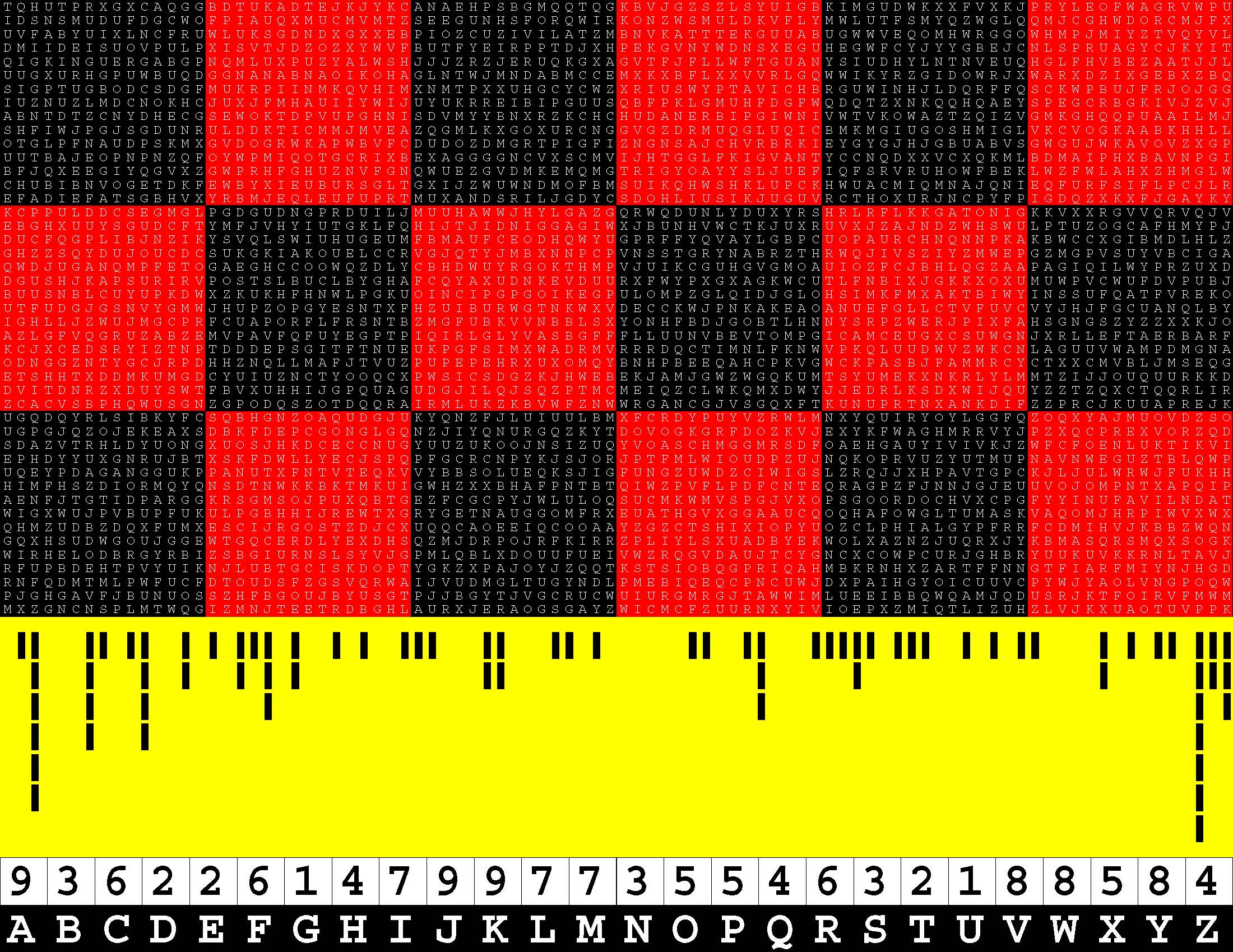
Introducing the perplexity of CATCHWORD which is to classic wordsearch as CHESS is to checkers.
Classic wordsearch gives you an itemized LIST of what are presumed to be spelled out words. Your so-called challenge is to locate each of the items expounded CONTIGUOUSLY across, down, and diagonally within a rectangular array of alphabetic letters. Ho hum. How utterly boring! Classic wordsearch is rote pattern recognition. Why waste your time trying to find some needles in a haystack? |
Classic wordsearch does not teach you anything in any way whatsoever.
The so-called words on the list might just as well be GIBBERISH. Classic wordsearch is hardly cerebral at all. Catchwork, on the other hand, challenges you to find an UNDISCLOSED word --- or, more likely, and much more PUZZLINGLY, an undisclosed PAIR of words --- VARIOUSLY spelled out DISCONTIGOUSLY across EACH and EVERY 25-letter line of a 7-line block of text. Catchwork behooves you to keep a dictionary handy as you sublimablely build up your vocabulary. |

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
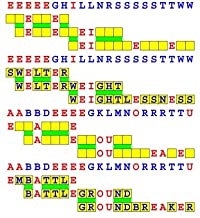
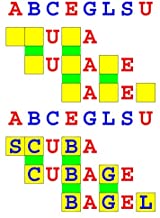
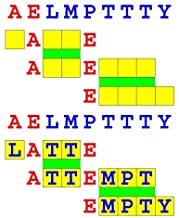
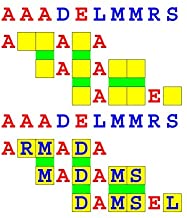
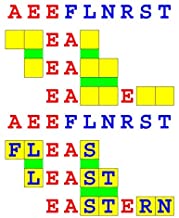
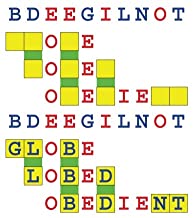
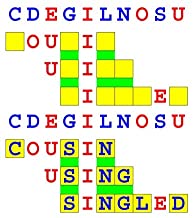
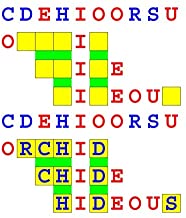
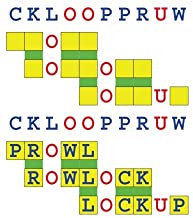
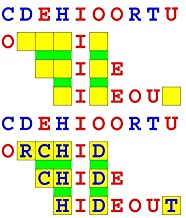
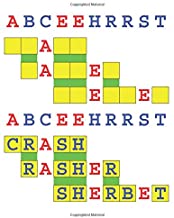
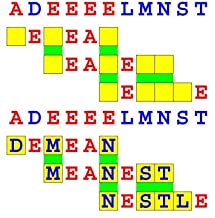
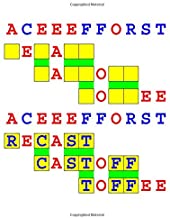
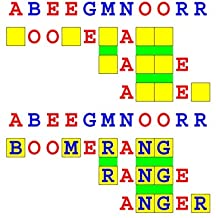
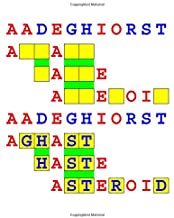
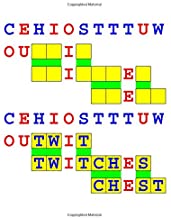
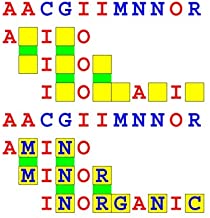
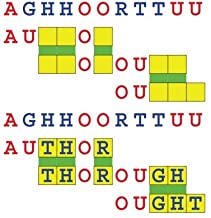
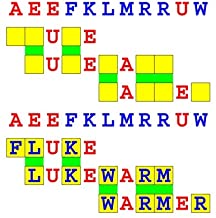
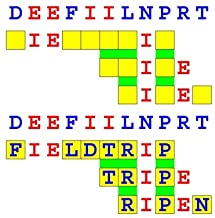
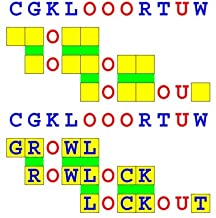
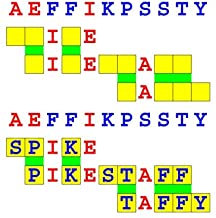
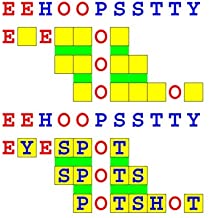
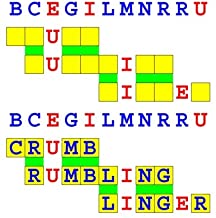
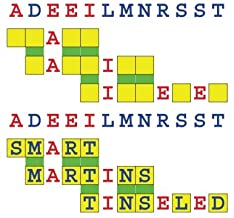
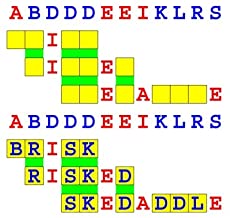
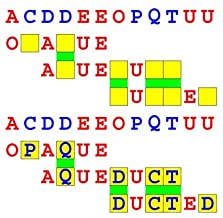
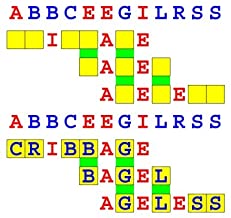
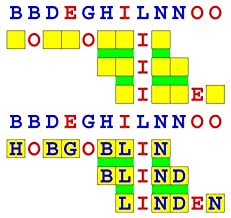
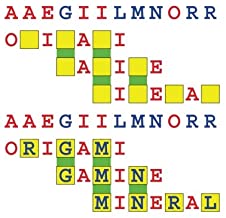
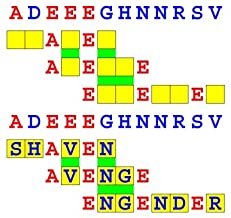
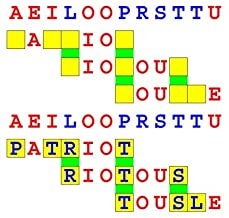
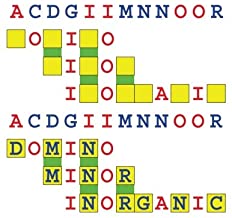
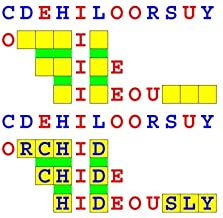
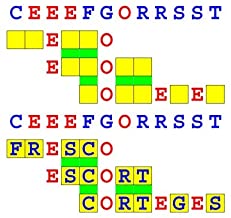
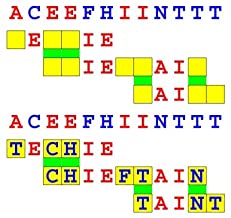
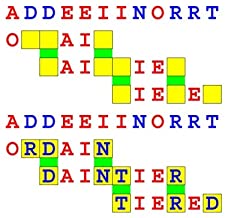
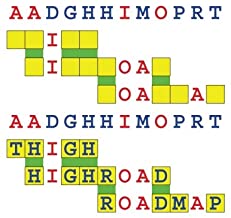
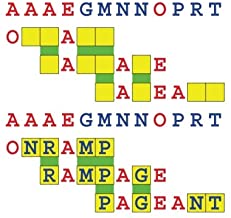
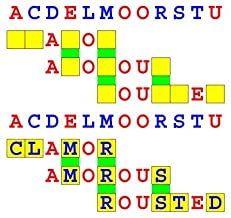
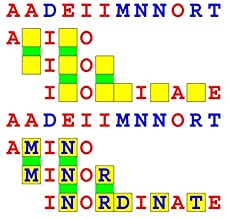
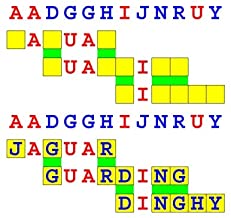
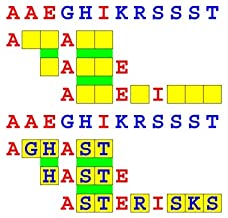
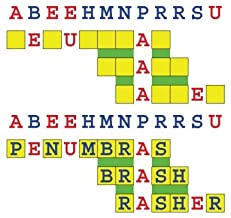
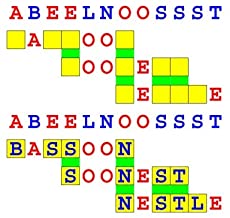
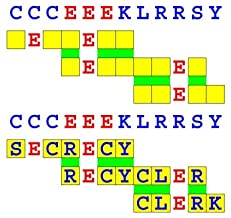
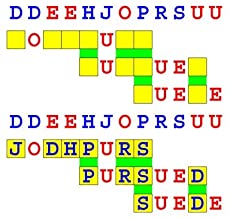
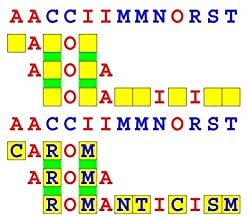
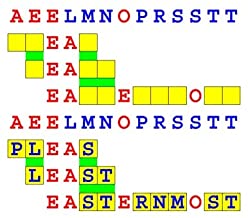
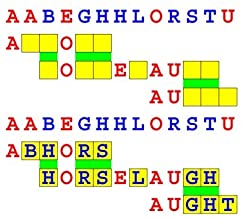
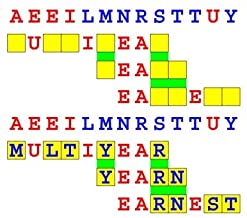
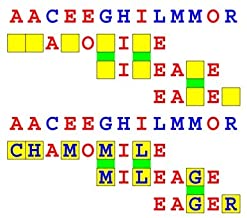
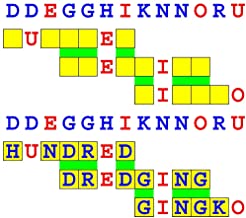
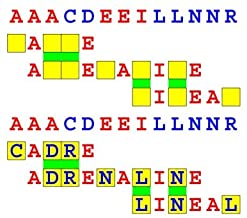
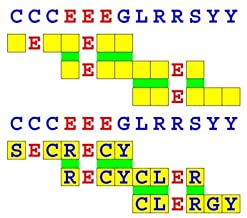
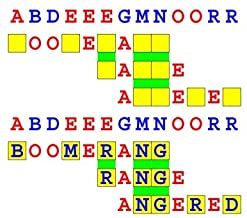
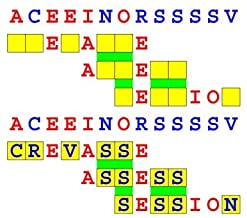
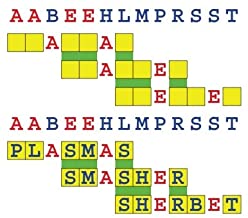
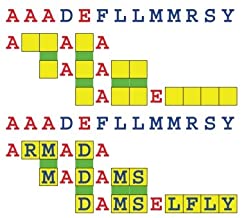
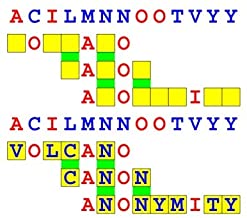
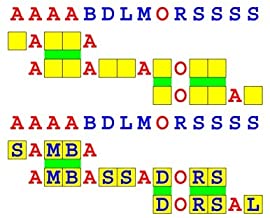
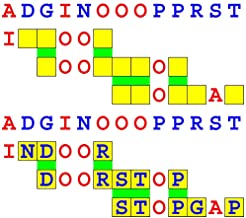
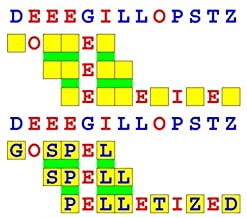
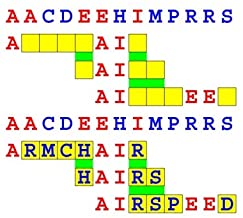
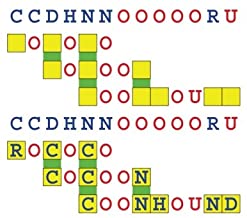
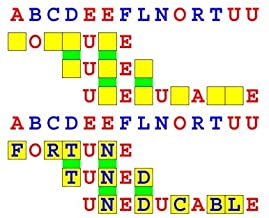
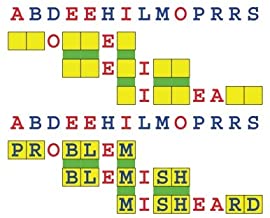
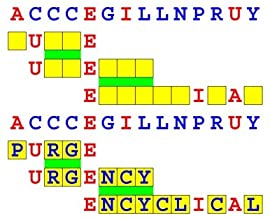
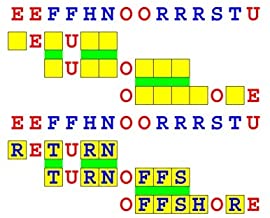
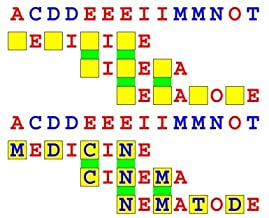
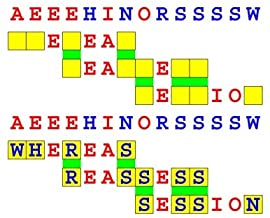
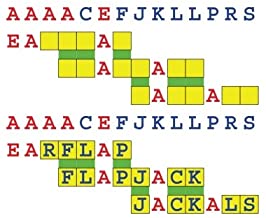
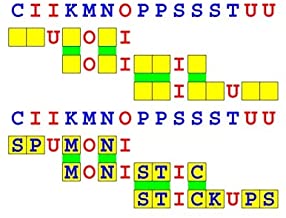
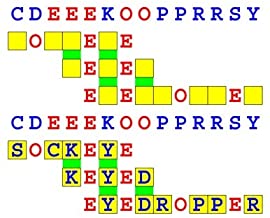
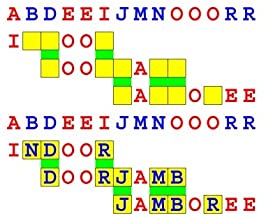
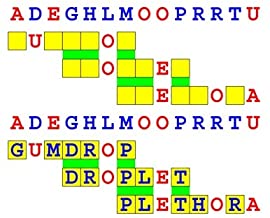
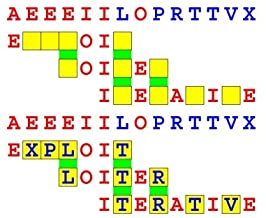
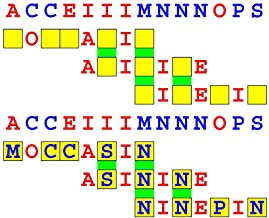
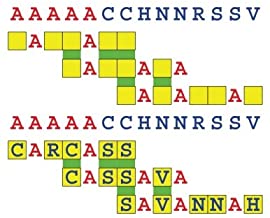
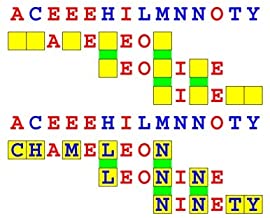
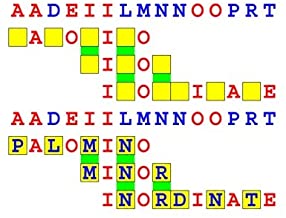
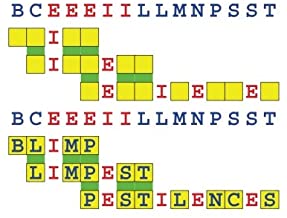
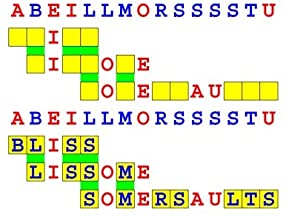
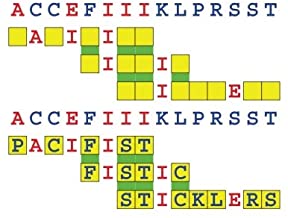
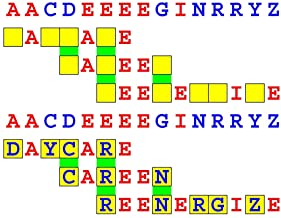
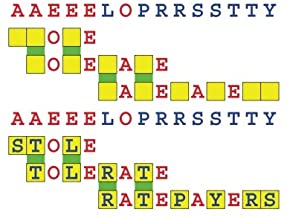
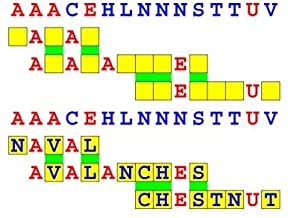
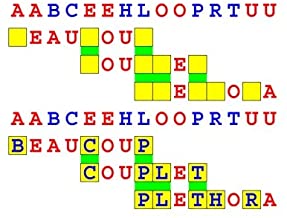
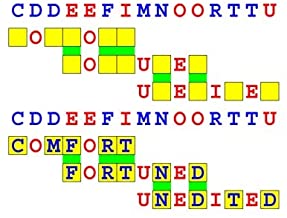
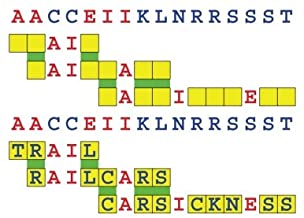
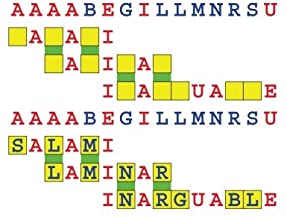
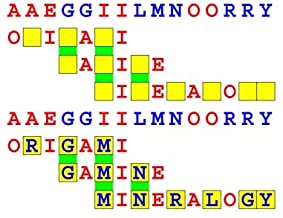
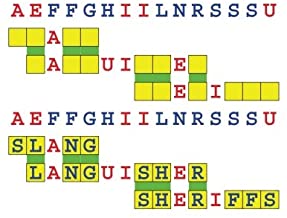
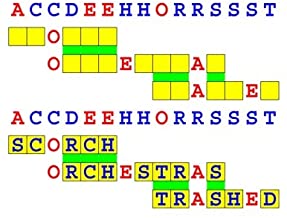
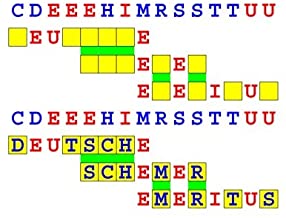
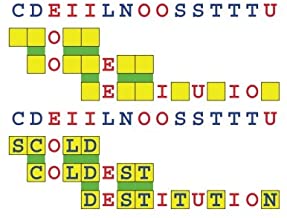
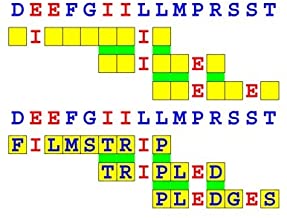
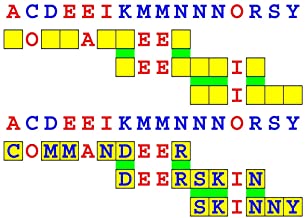
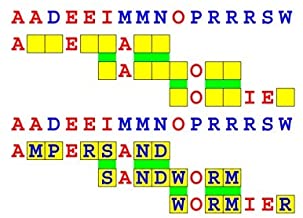
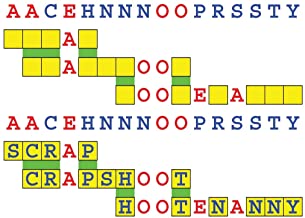
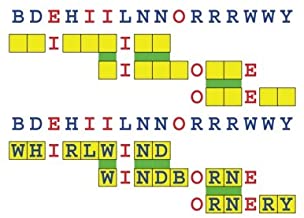
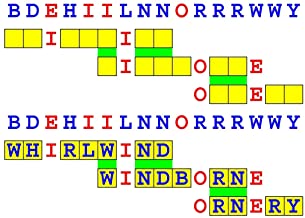
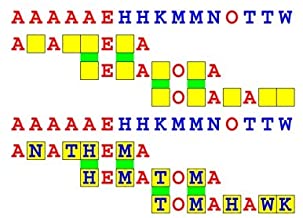
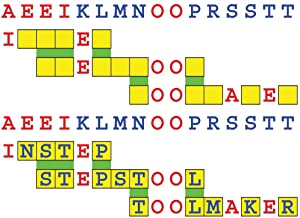
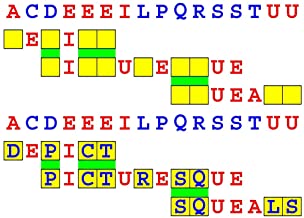
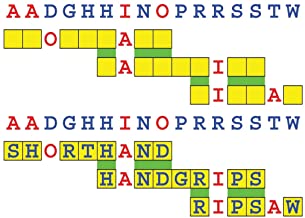
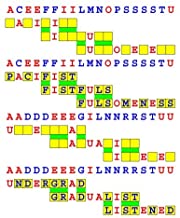
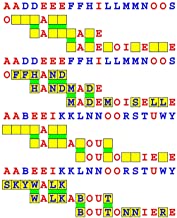
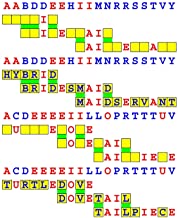
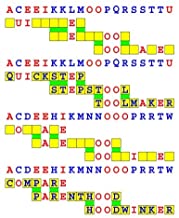
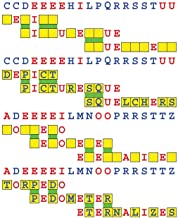
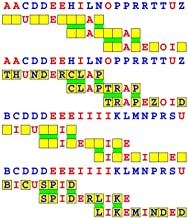
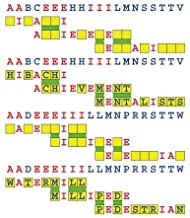
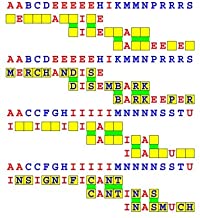
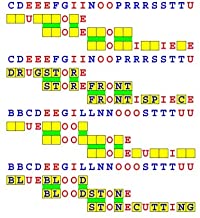
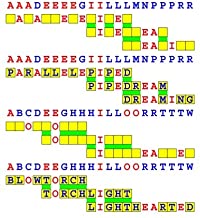
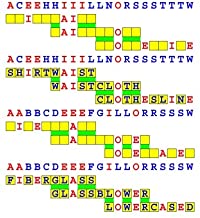
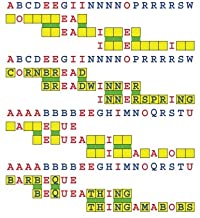
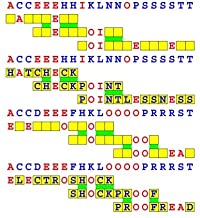
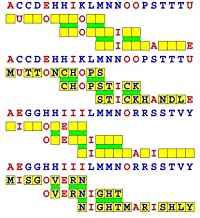
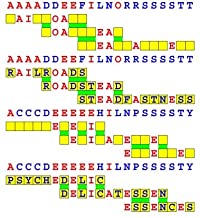
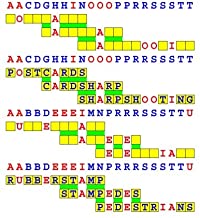
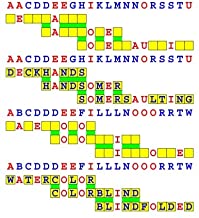
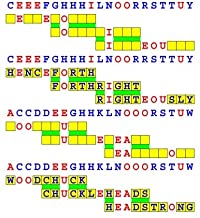
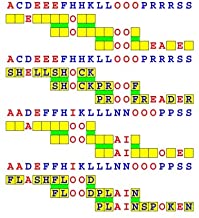
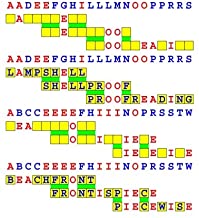
Joinword Puzzles by Francis Gurtowski
Take a once-a-day, sanity break
by enjoying these harmless, bite-sized fusions
of crossword & anagram puzzles.
|

|

|
|

|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|

|

|

|

|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|

|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|

|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|

|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|

|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|

|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|

|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||

|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|

|
|

|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|

|

|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||

|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|

|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||

|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||

|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|

|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|

|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||

|
|
|
|

|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||

|
|

|

|

|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||

|
|
|

|

|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|

|

|

|

|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|

|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|

|
|
|

|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|

|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|

|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
293,706 Loch Ness Puzzles by Francis Gurtowski
|
This is yet another serious, serious series of books authored by Francis Gurtowski.
The prolific author is an authentic, ancient coder, going all the way back to IBM Poughkeepsie (Building 705, no less, second floor) and the heyday of OS/360, Robert Rex Seeber Jr. and the horizontal-microcoded System/360 Model 50, coding pads and the coding-pad veto, punch cards and keypunch machines, and self-modifying code. Francis Gurtowski is also a self-styled Henry Ford of contemporary, do-it-yourself, print-on-demand, book publishing. Henry Ford is synonymous with the assembly line, a perfected process for swiftly turning out a series of ingenious, finished products in a foolproof, mechanically-efficient manner. All 999 of these sequels take full advantage of (Amazon) Kindle Direct Publishing's twin, generous, upper limits of 590 bound-and-paperbacked, 8.5x11-inch pages. |
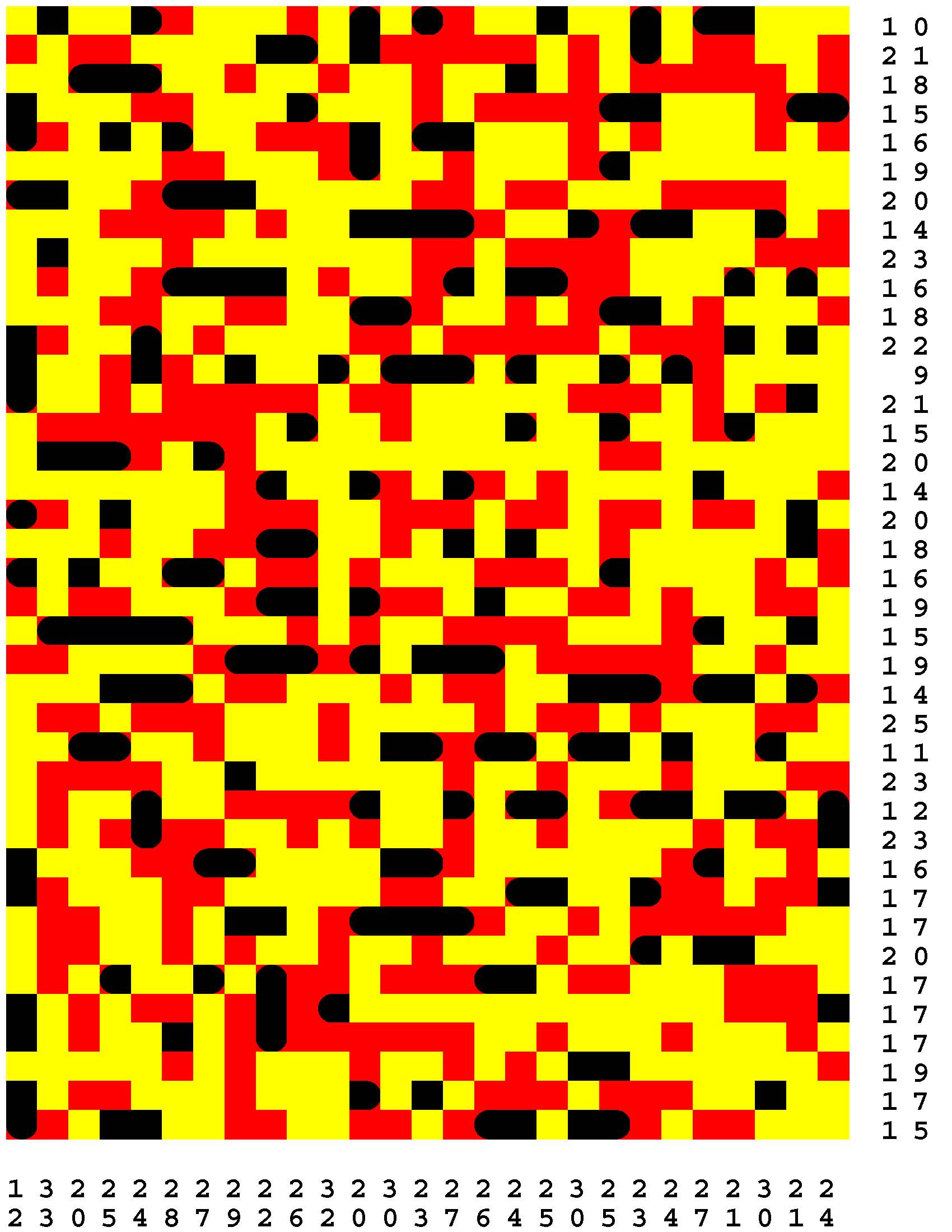
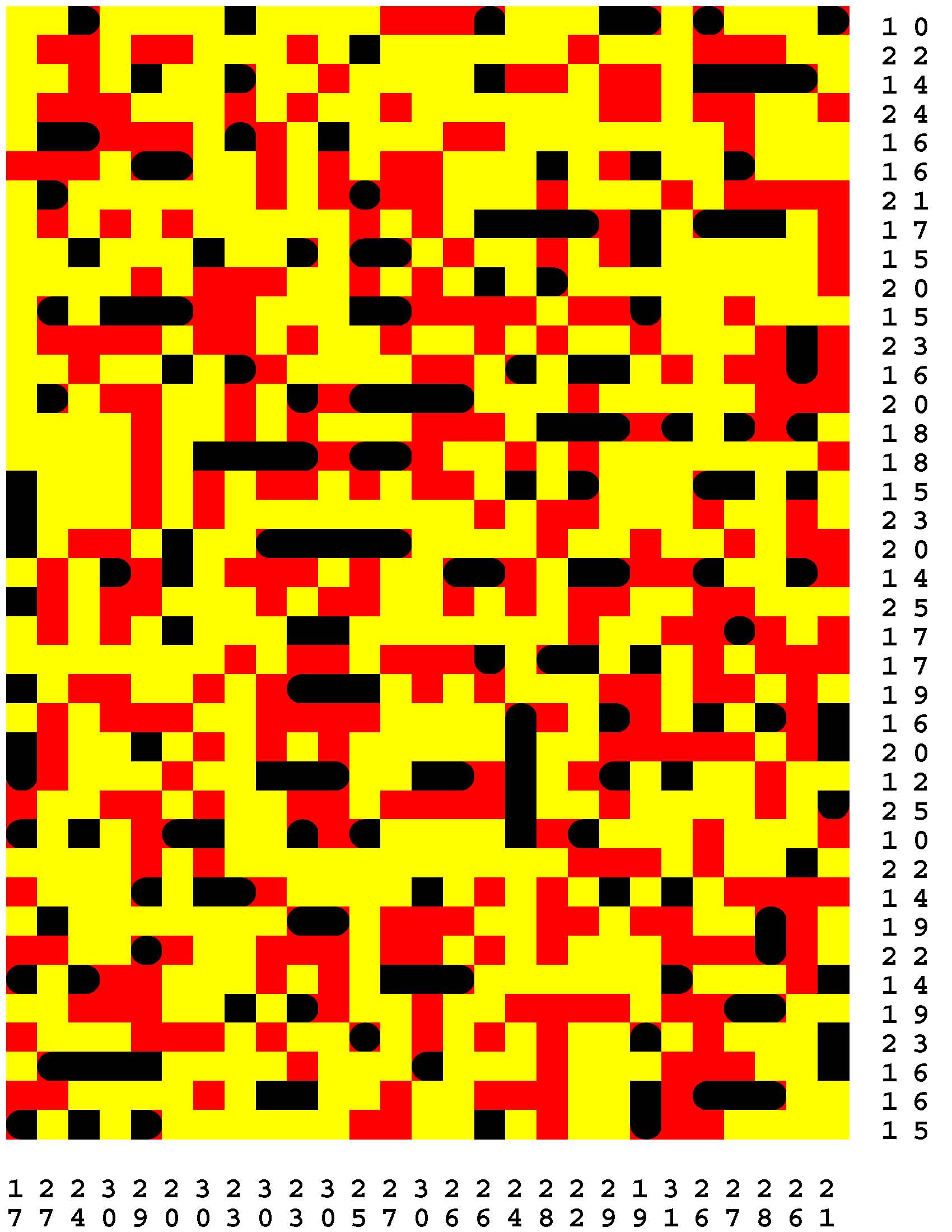
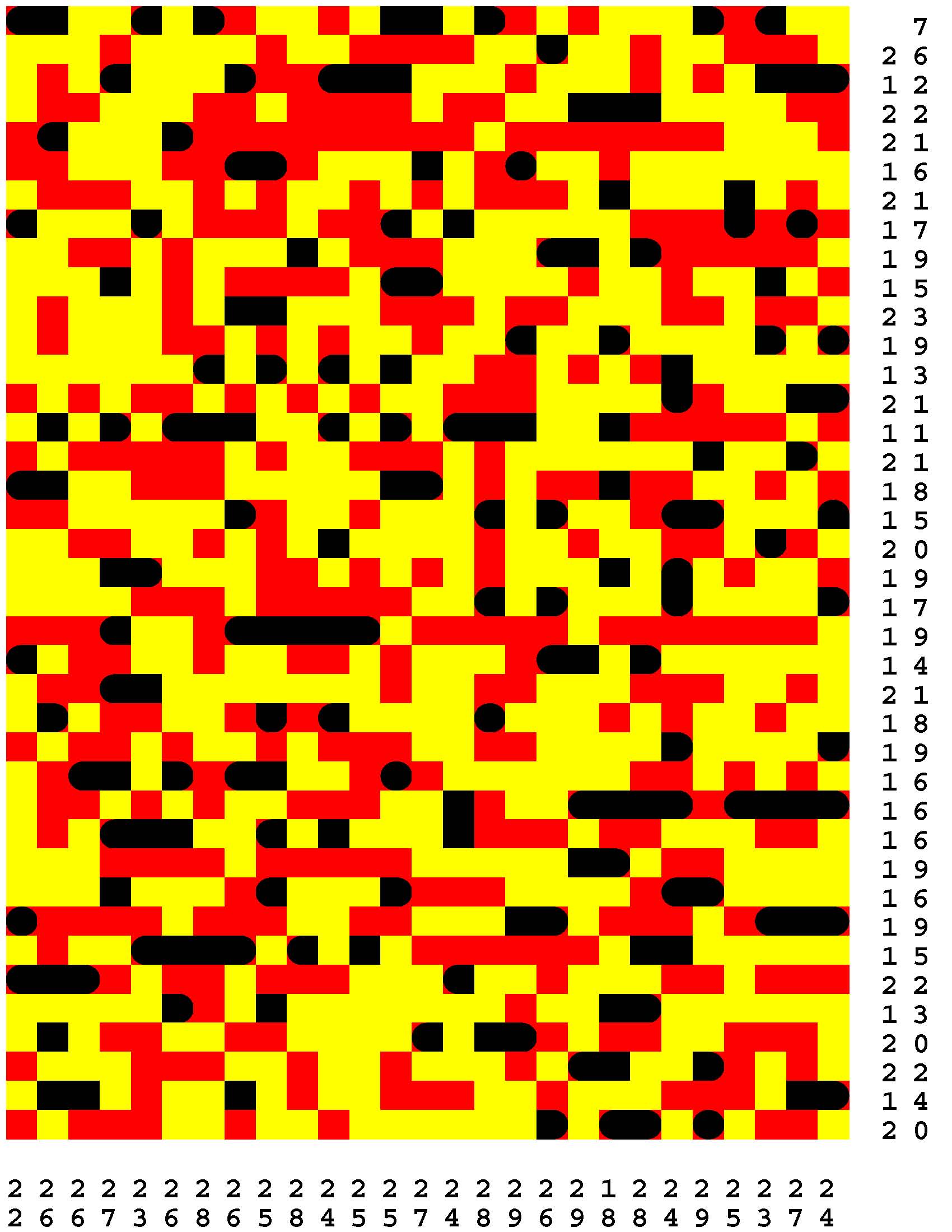
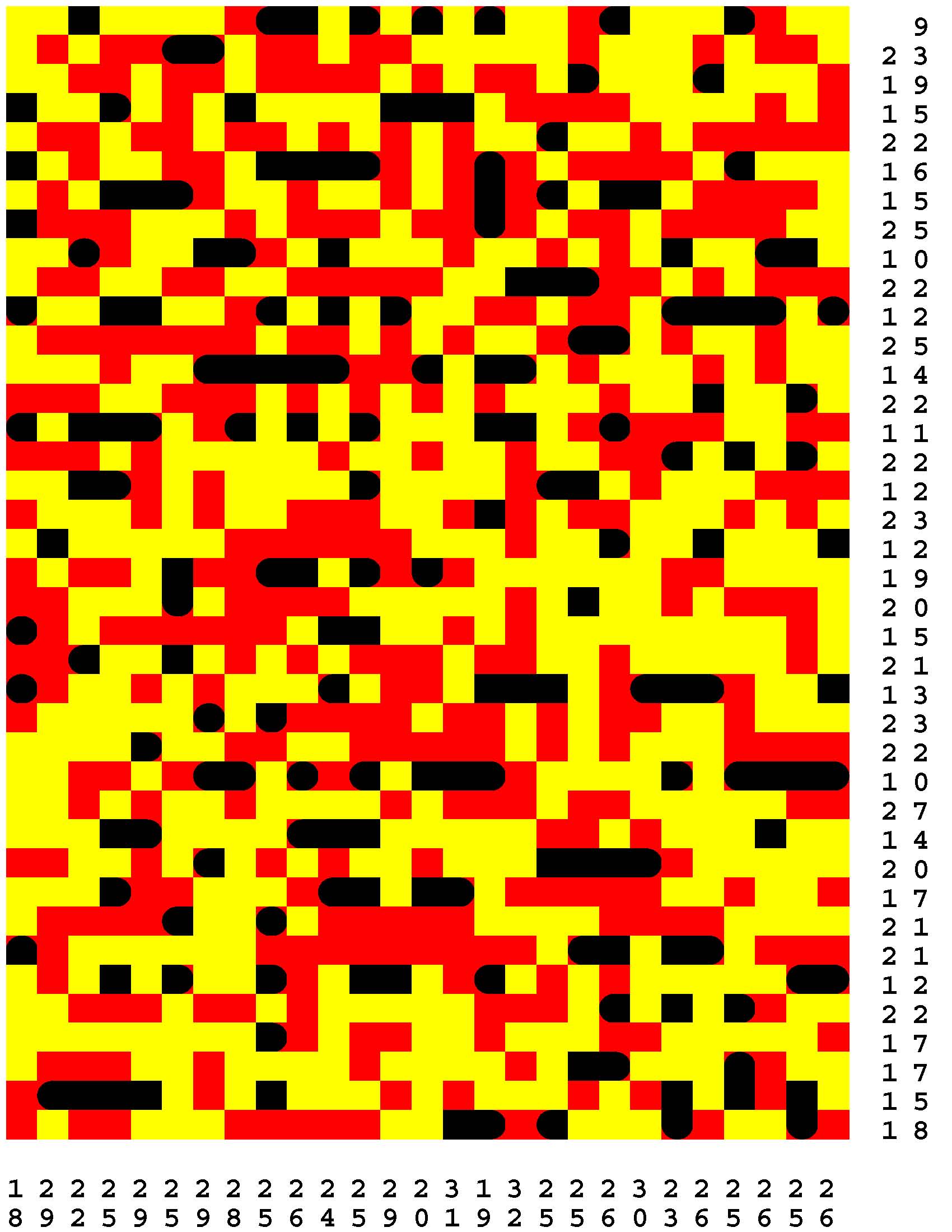
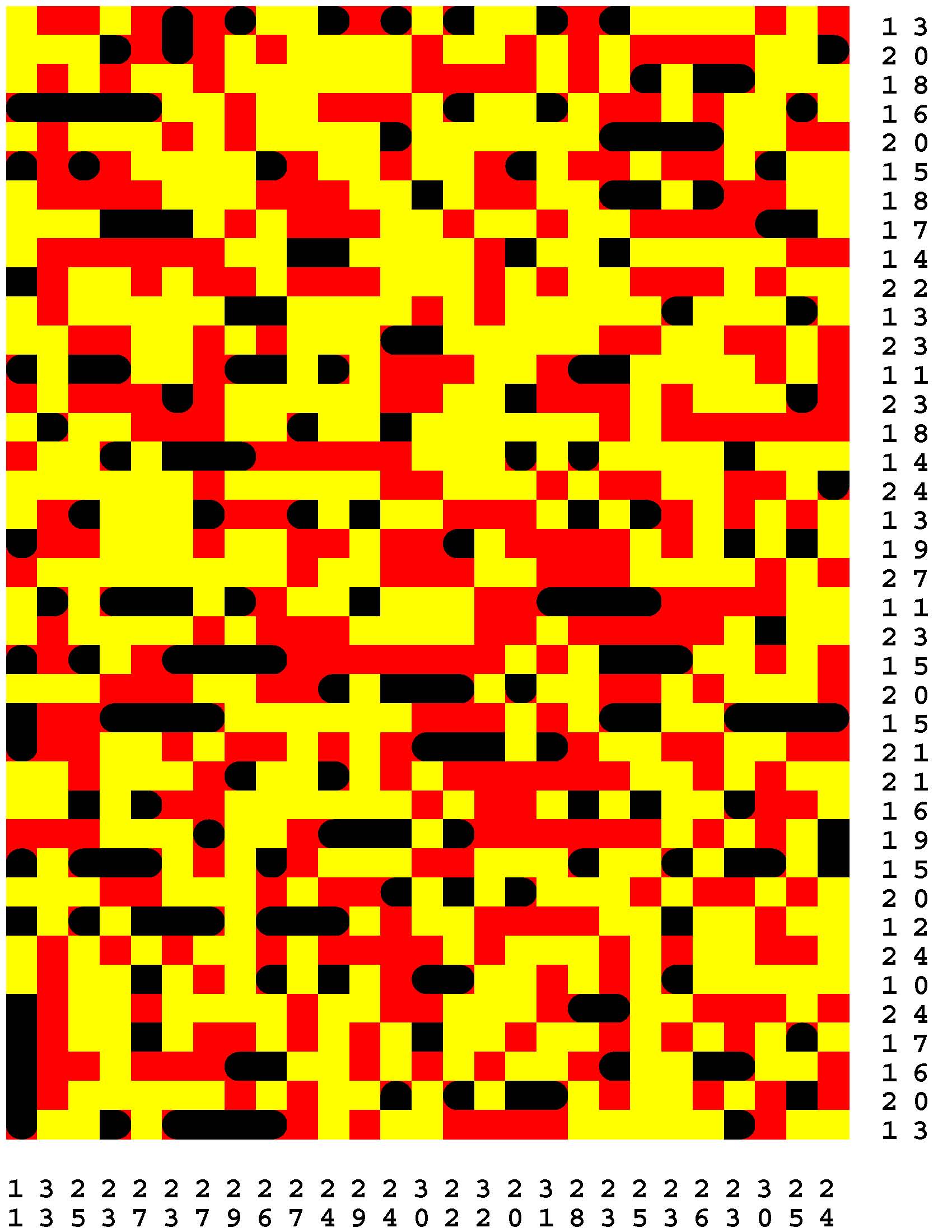
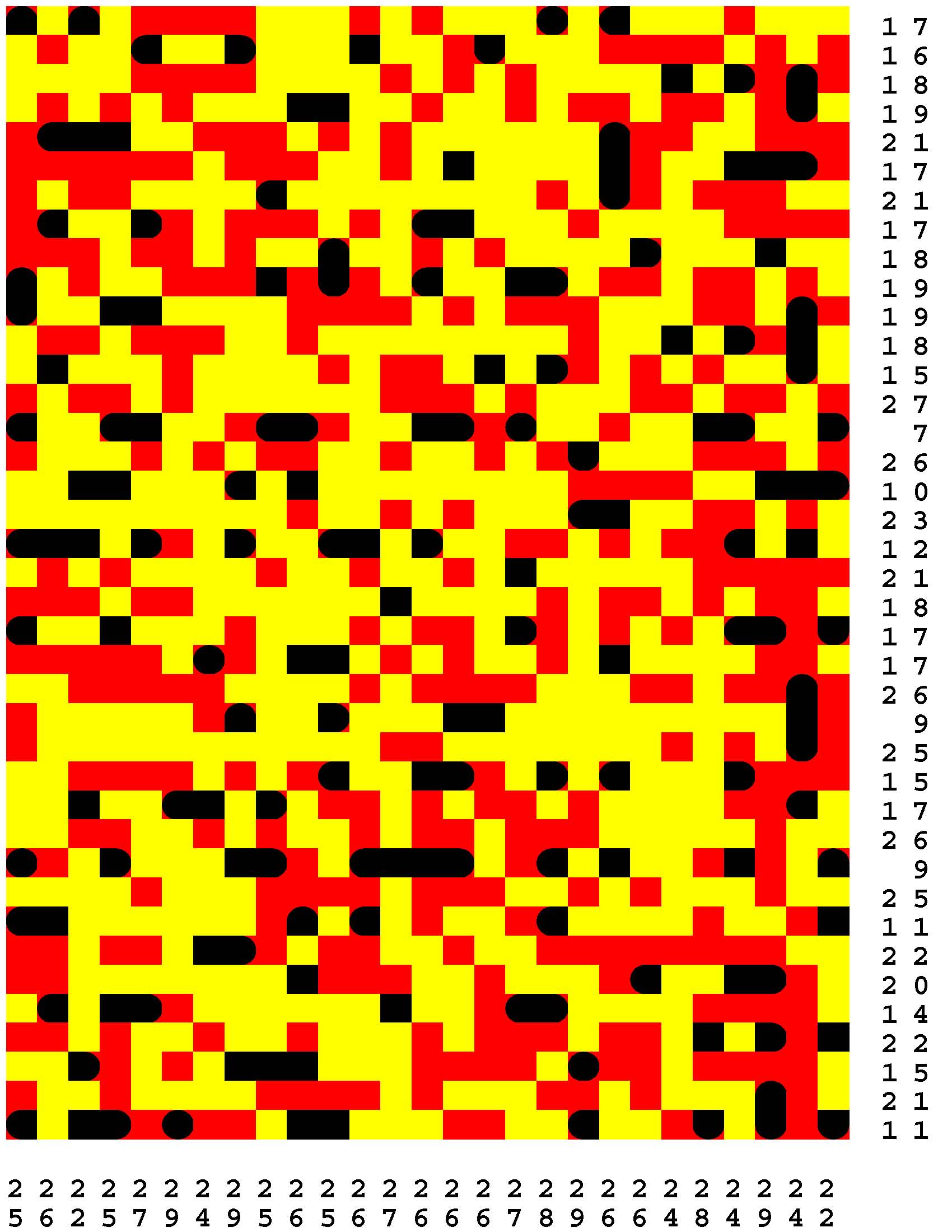
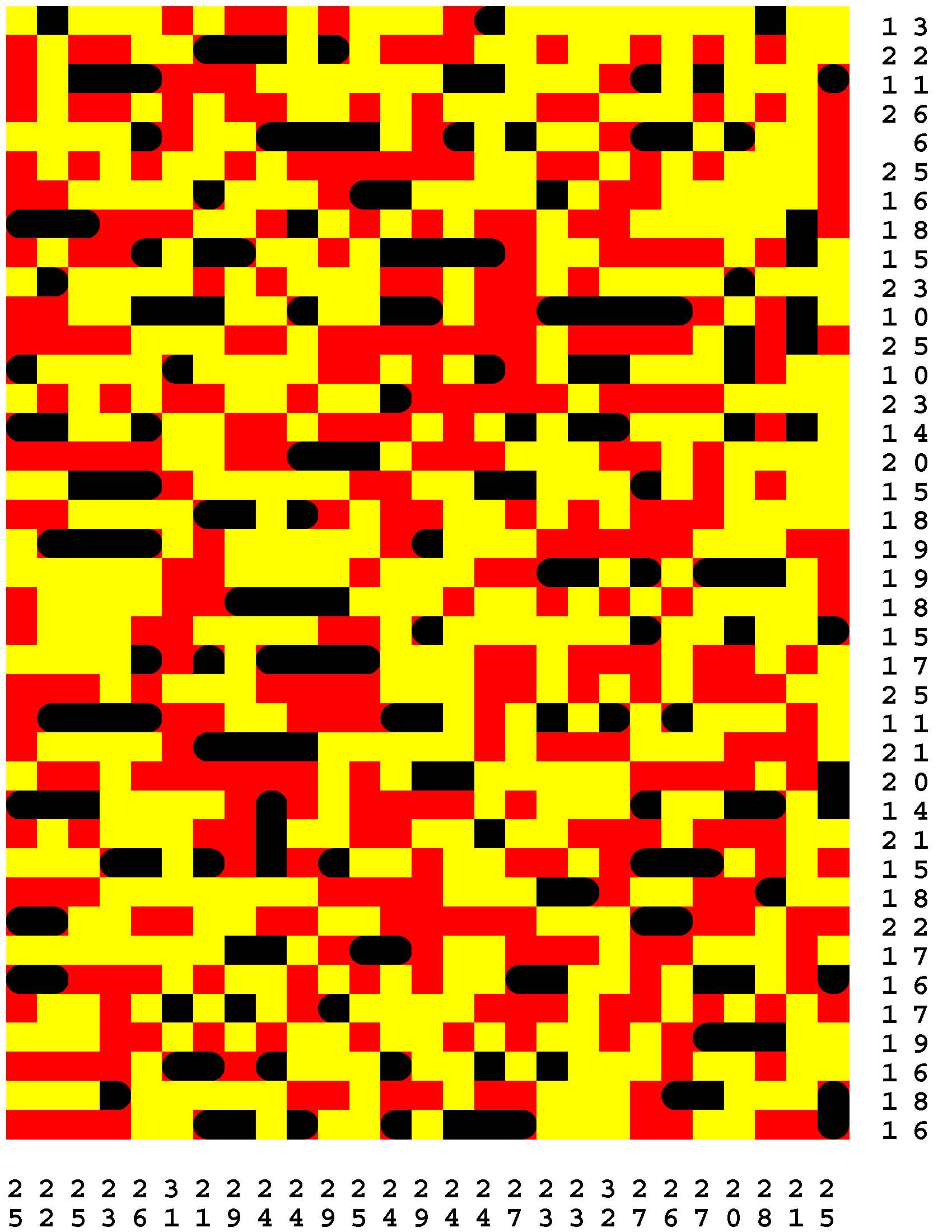
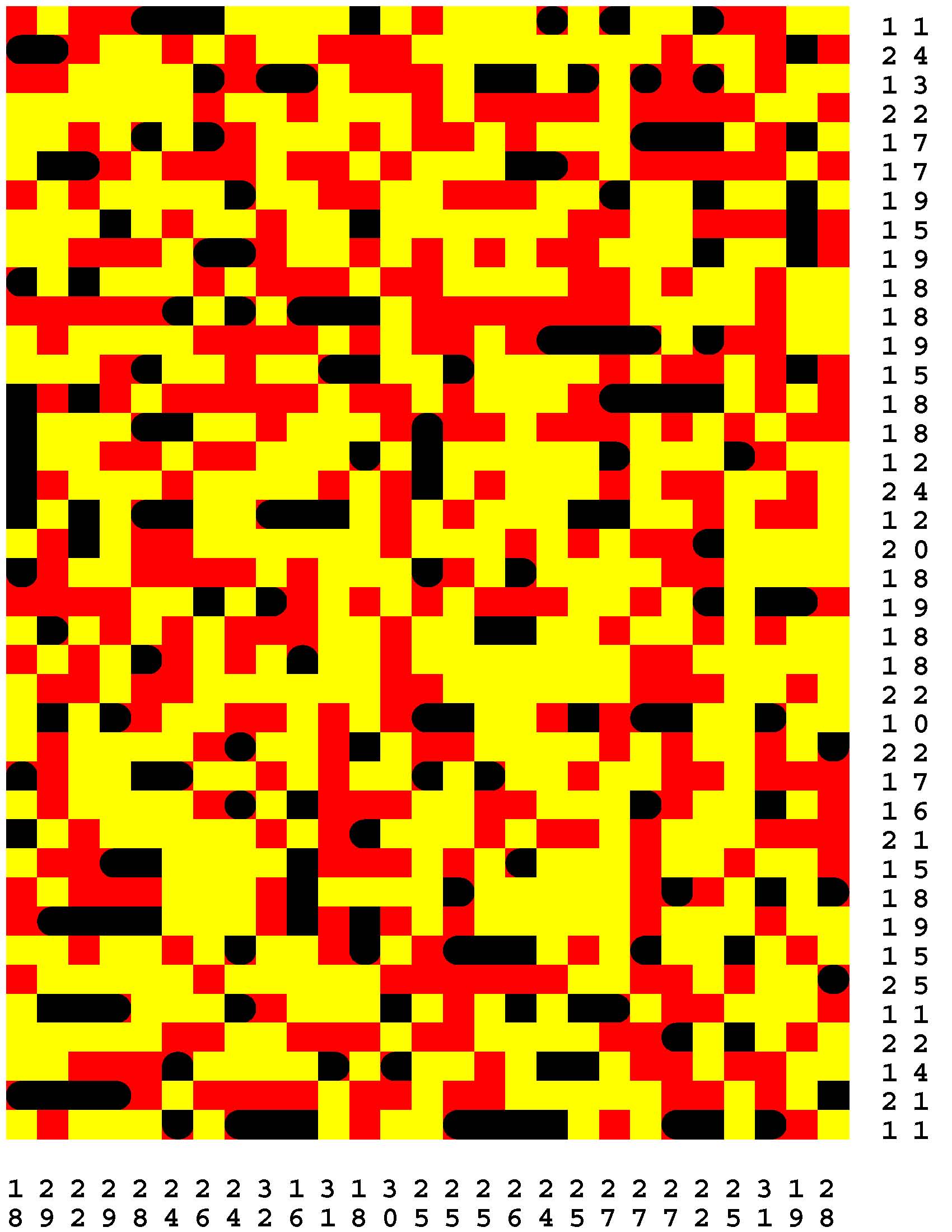
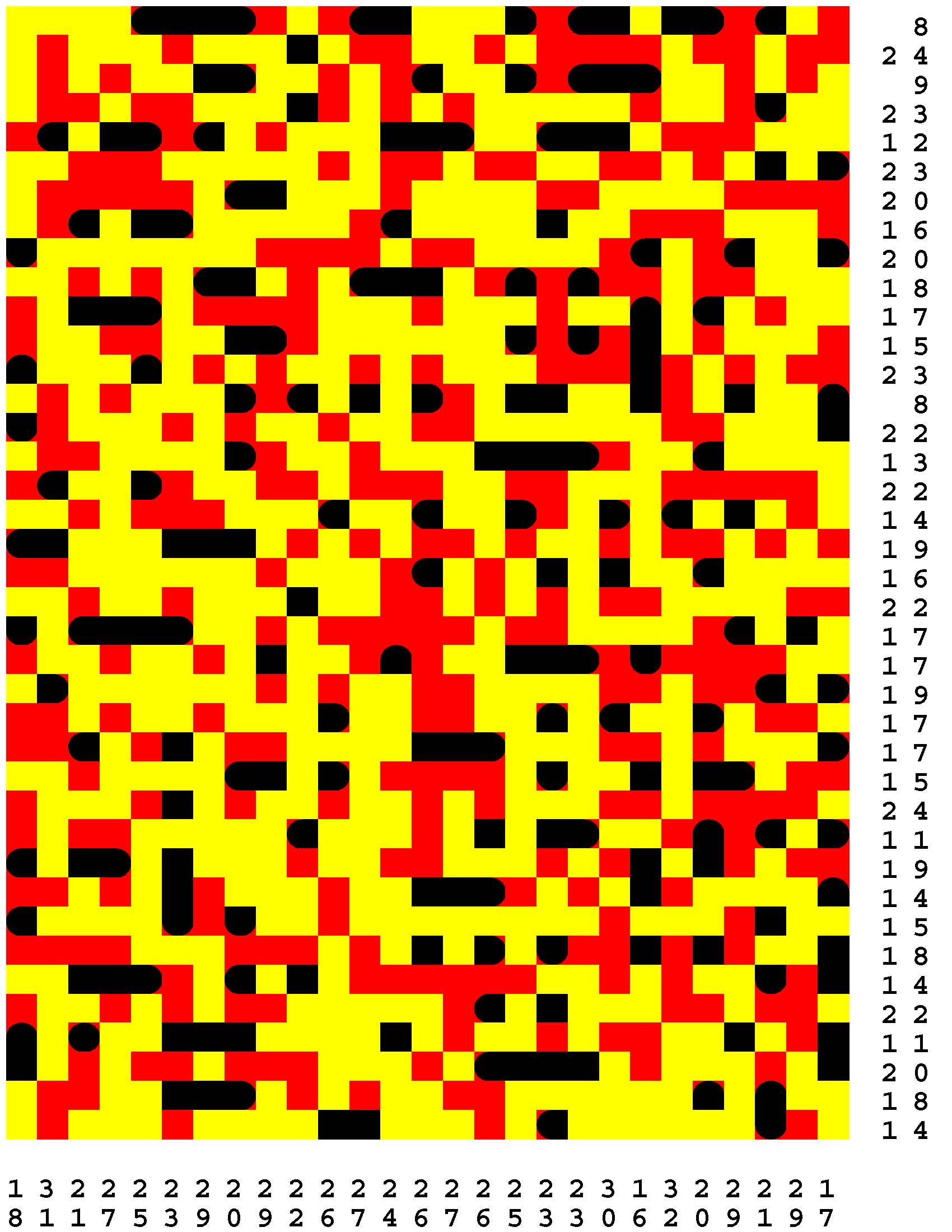
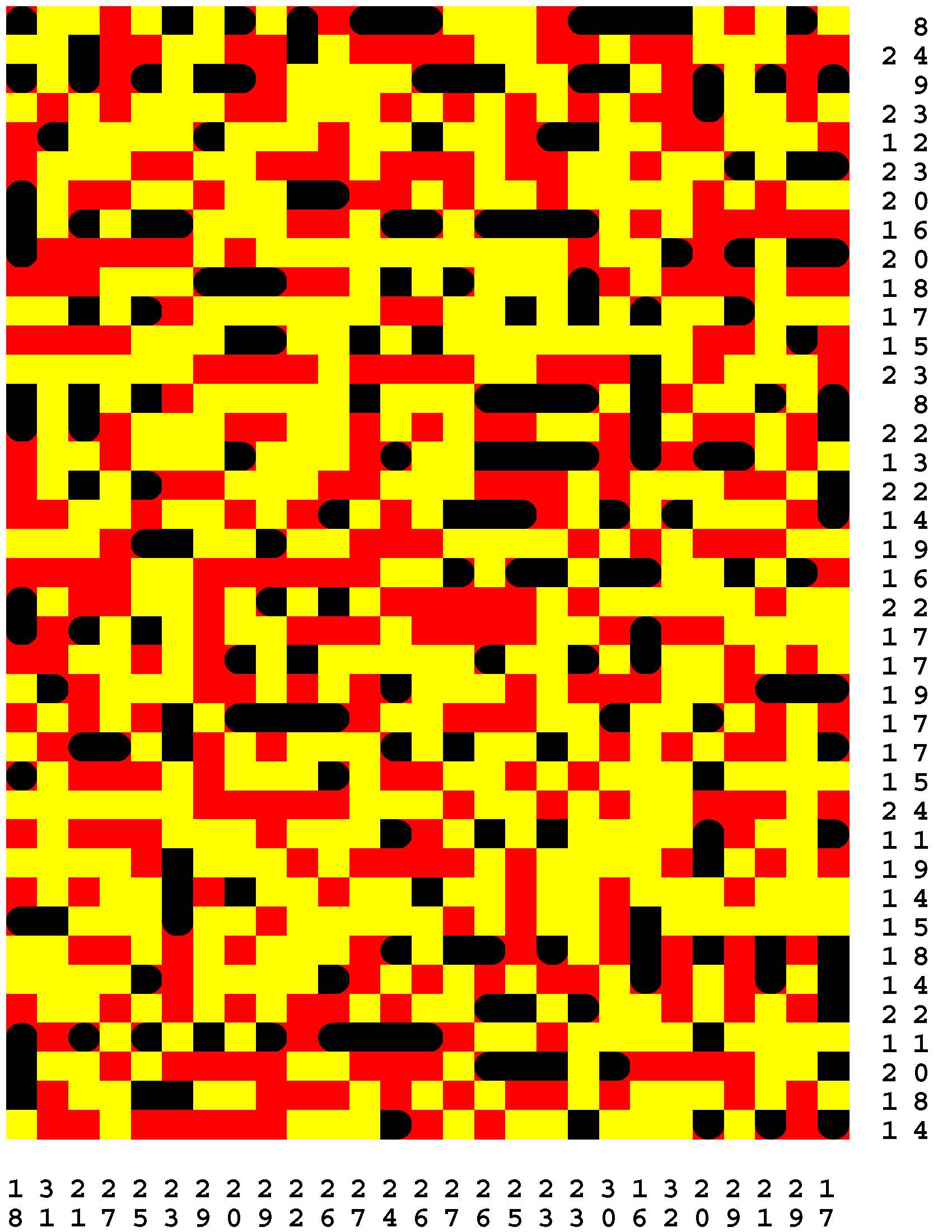
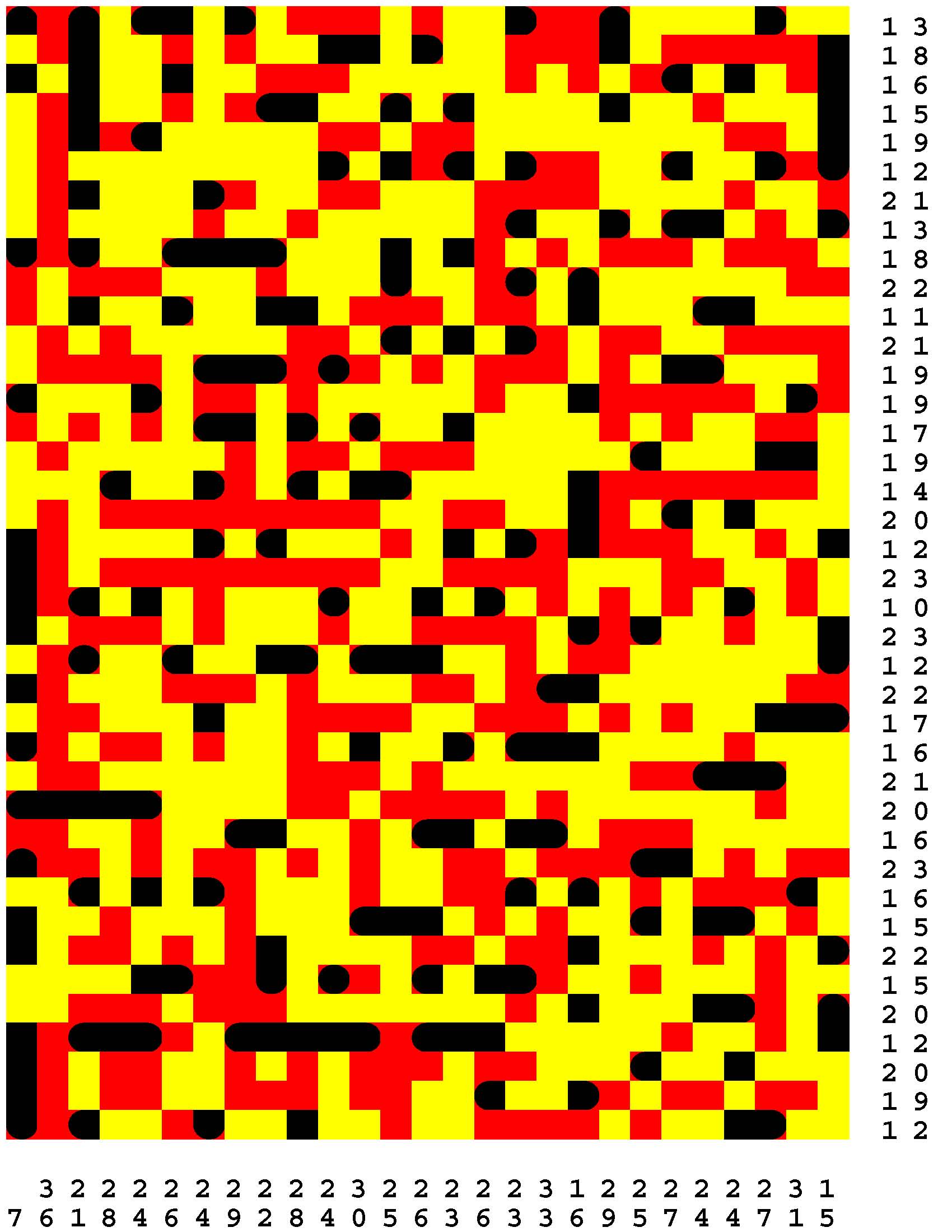
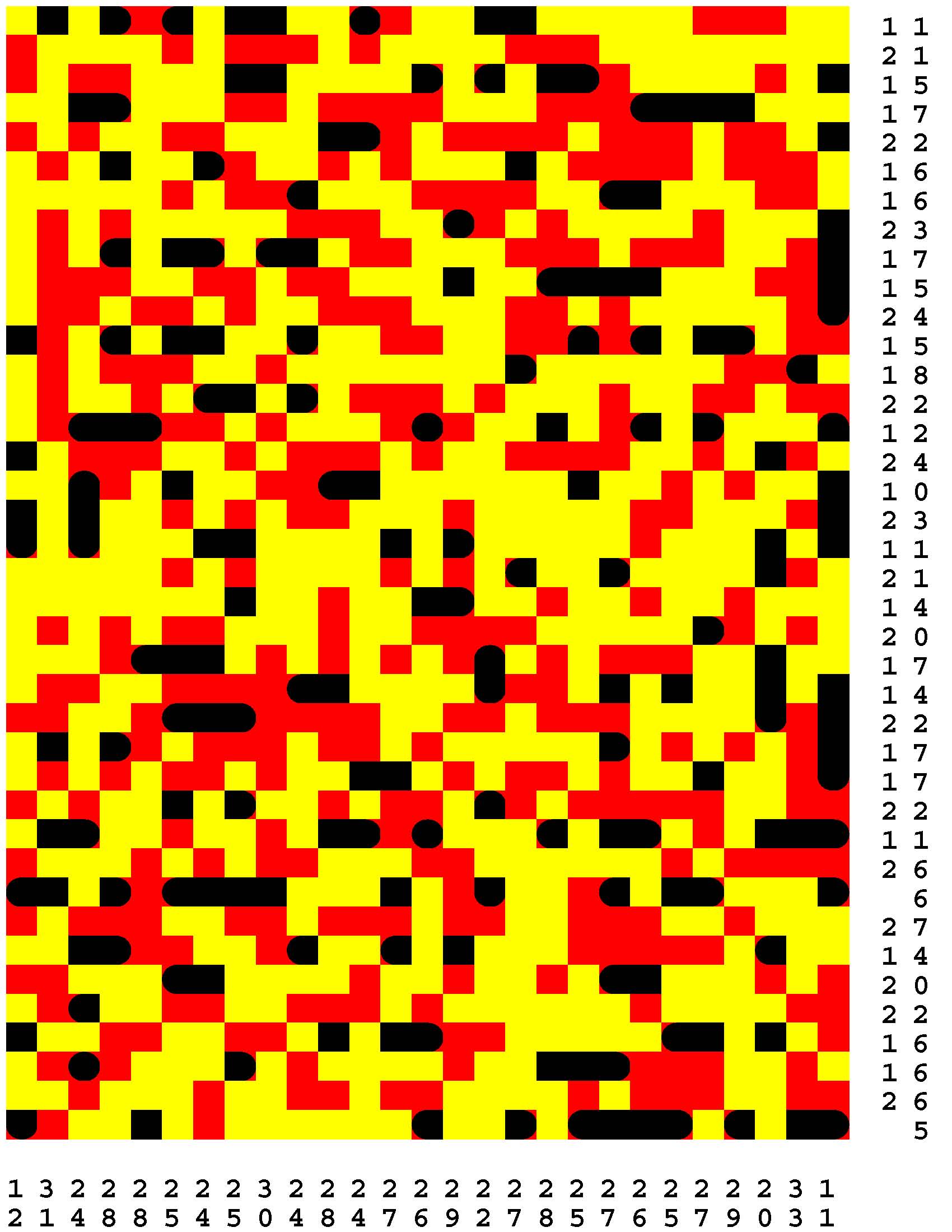
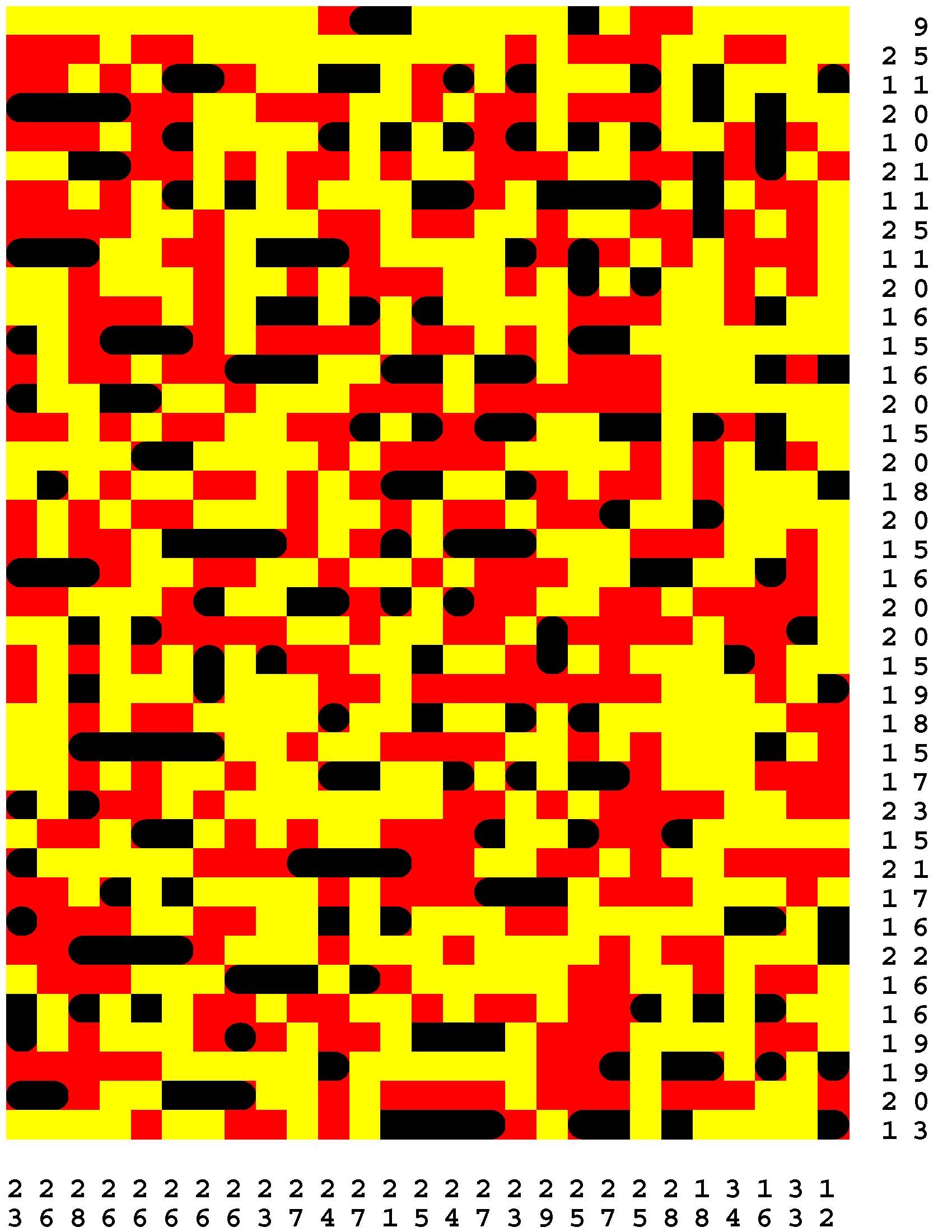
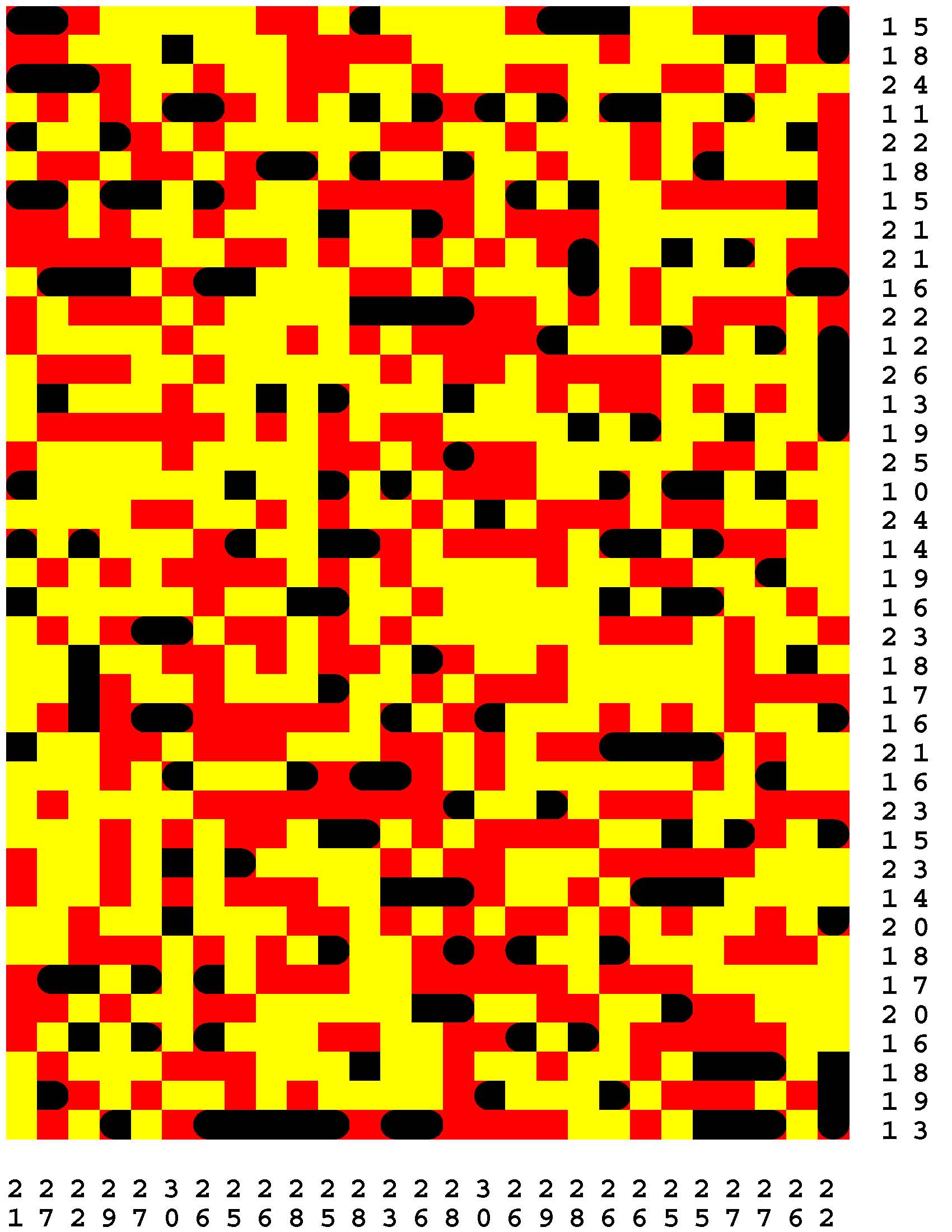
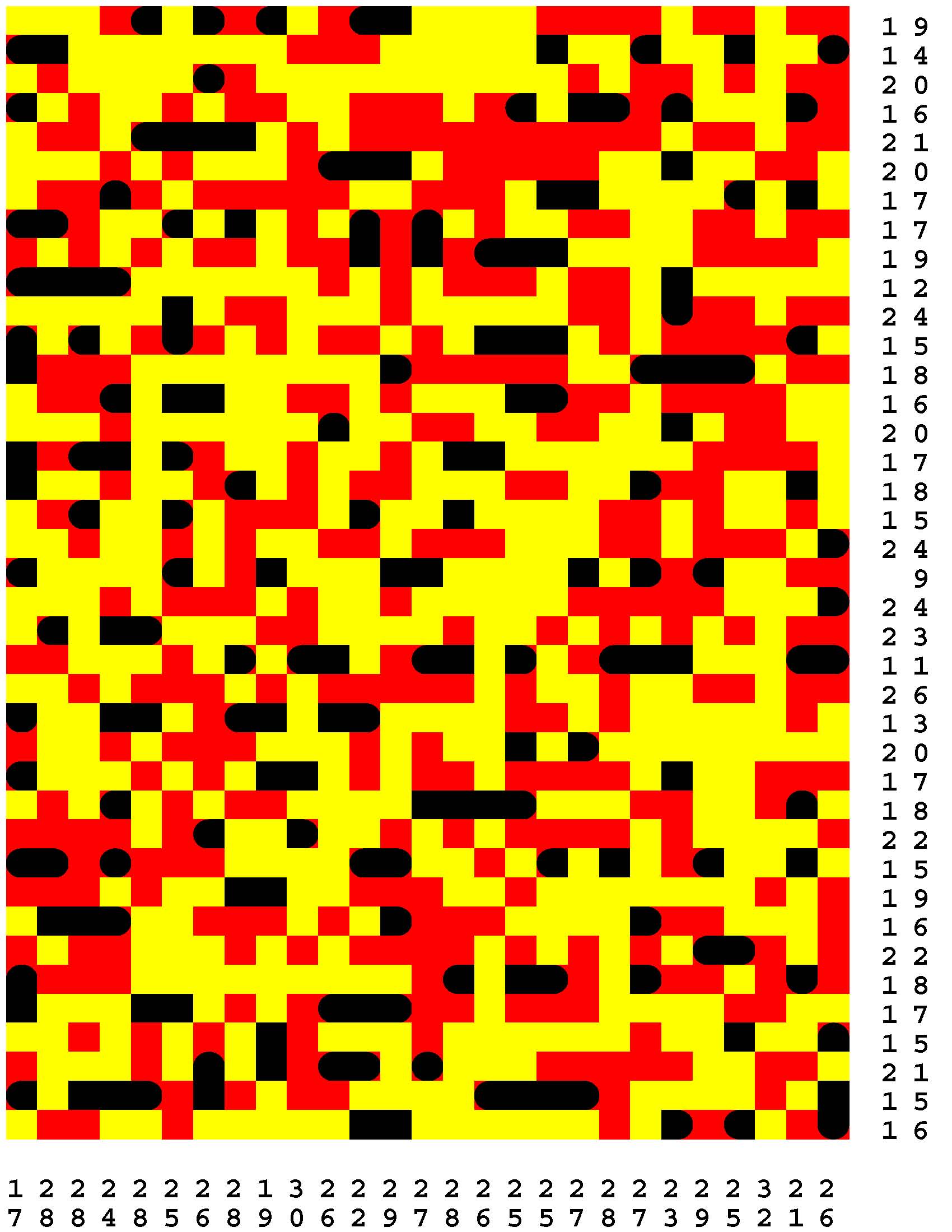
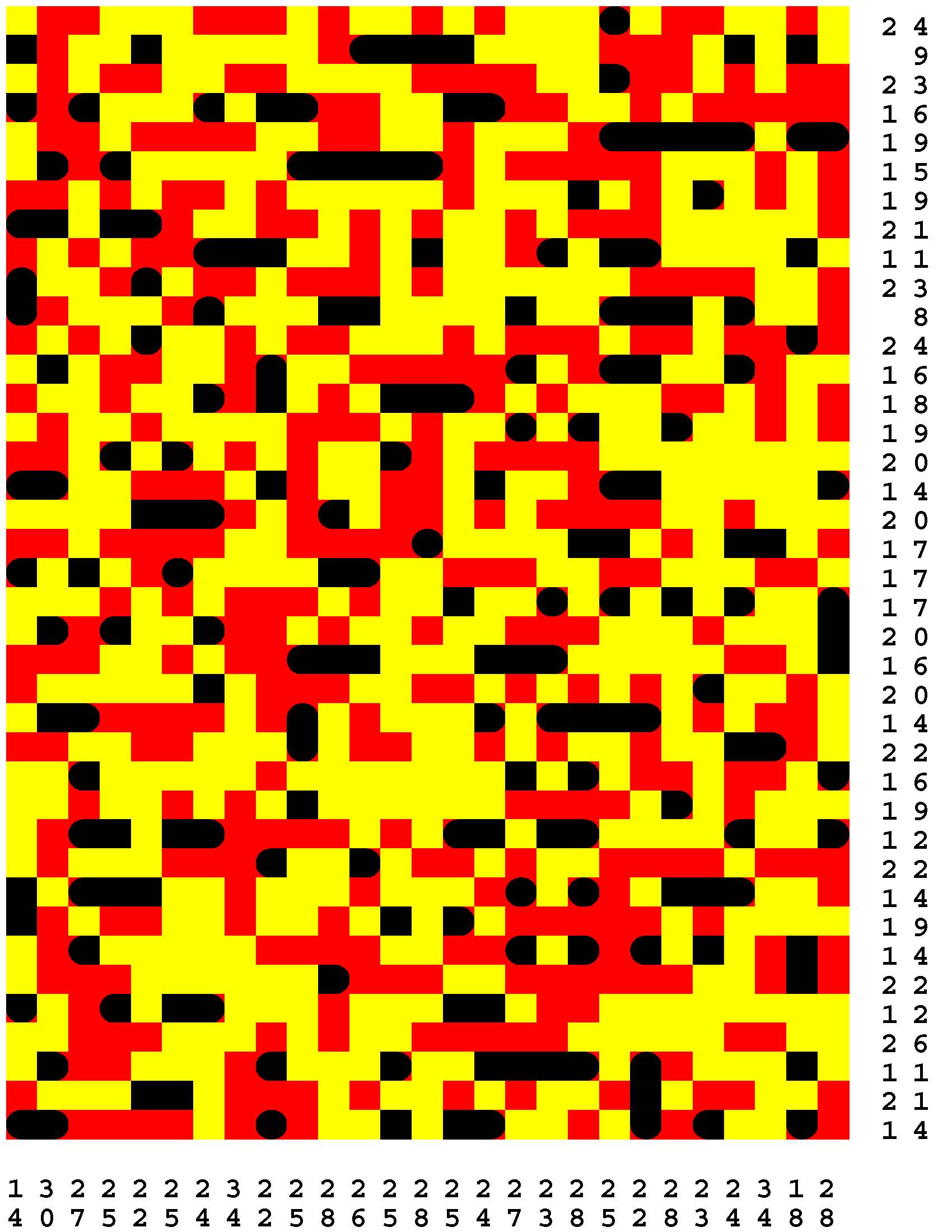
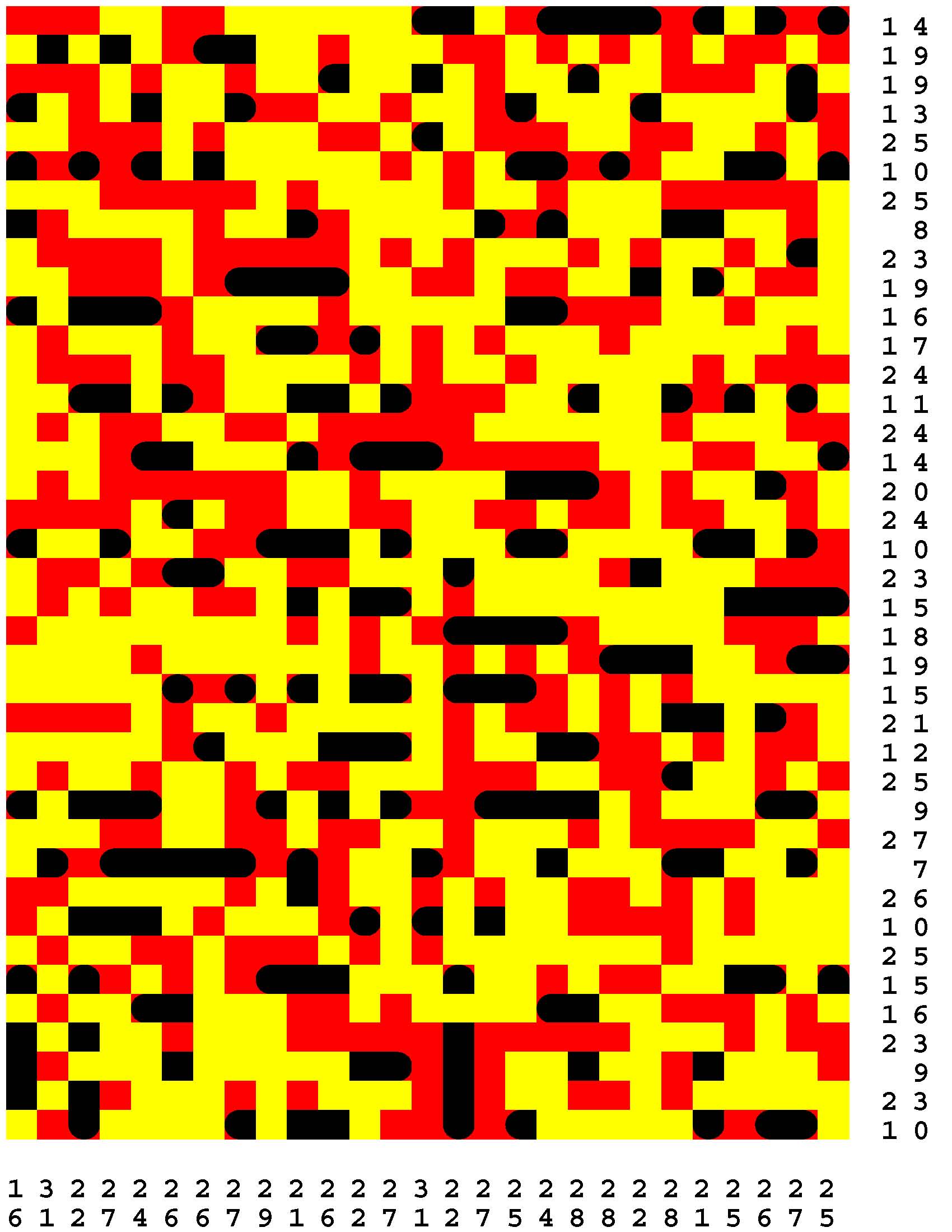
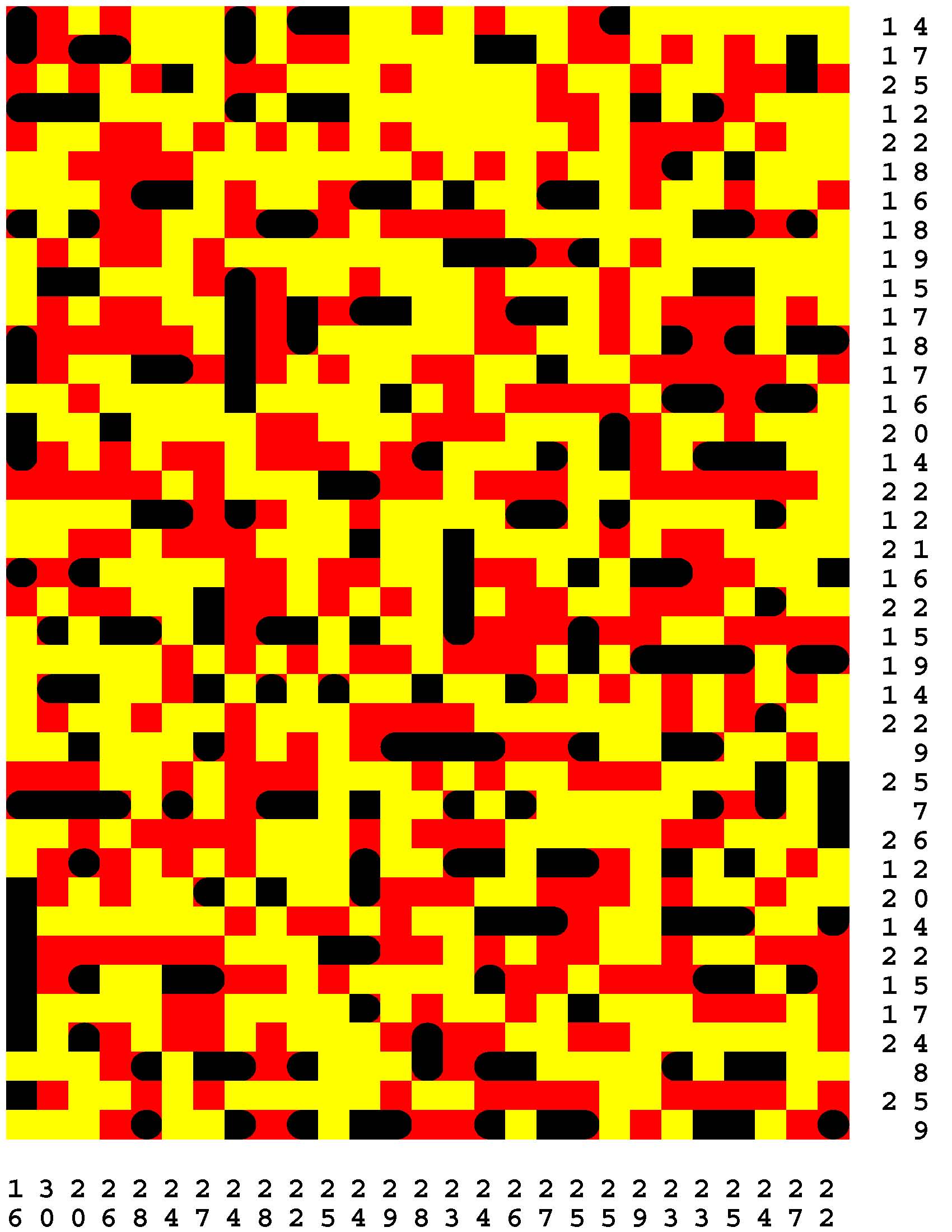
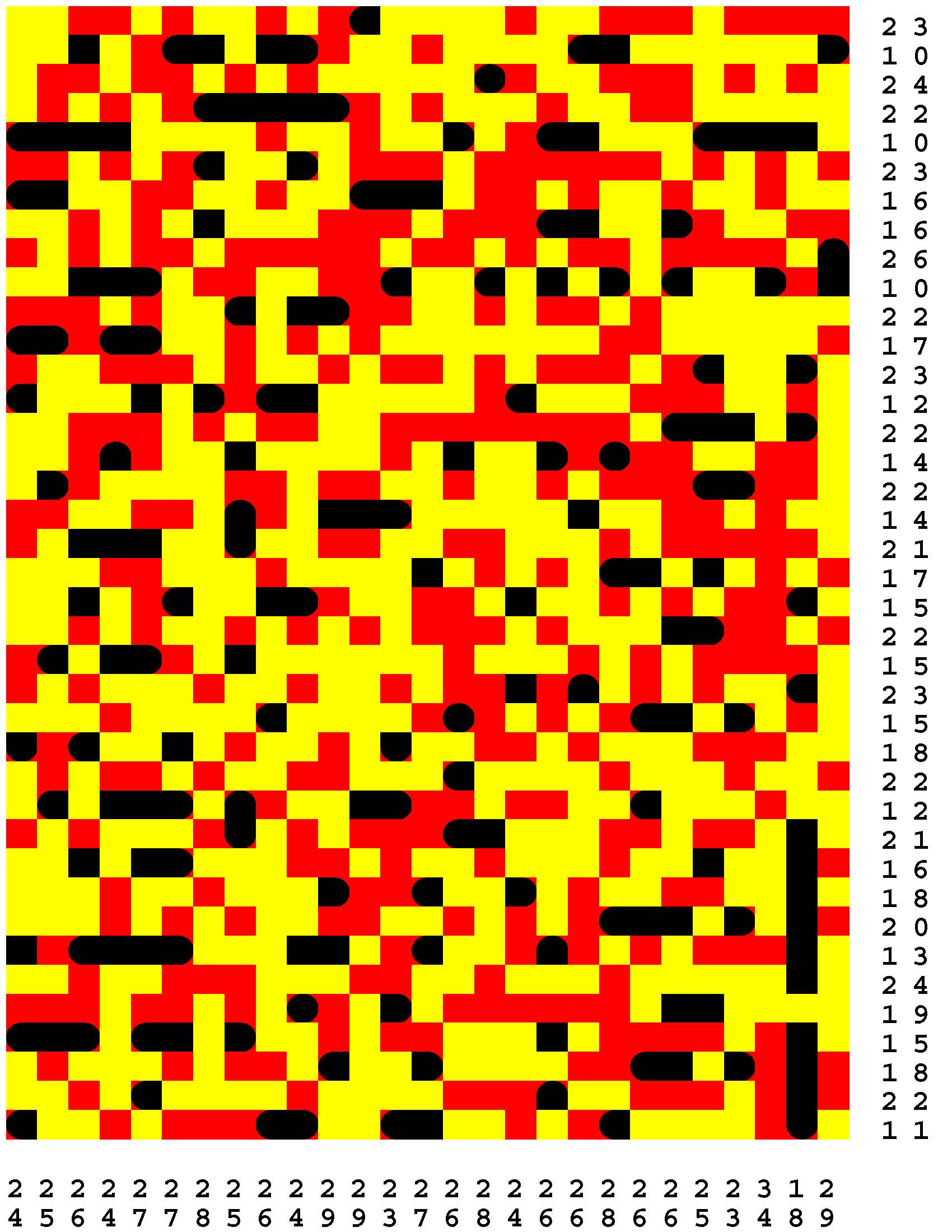
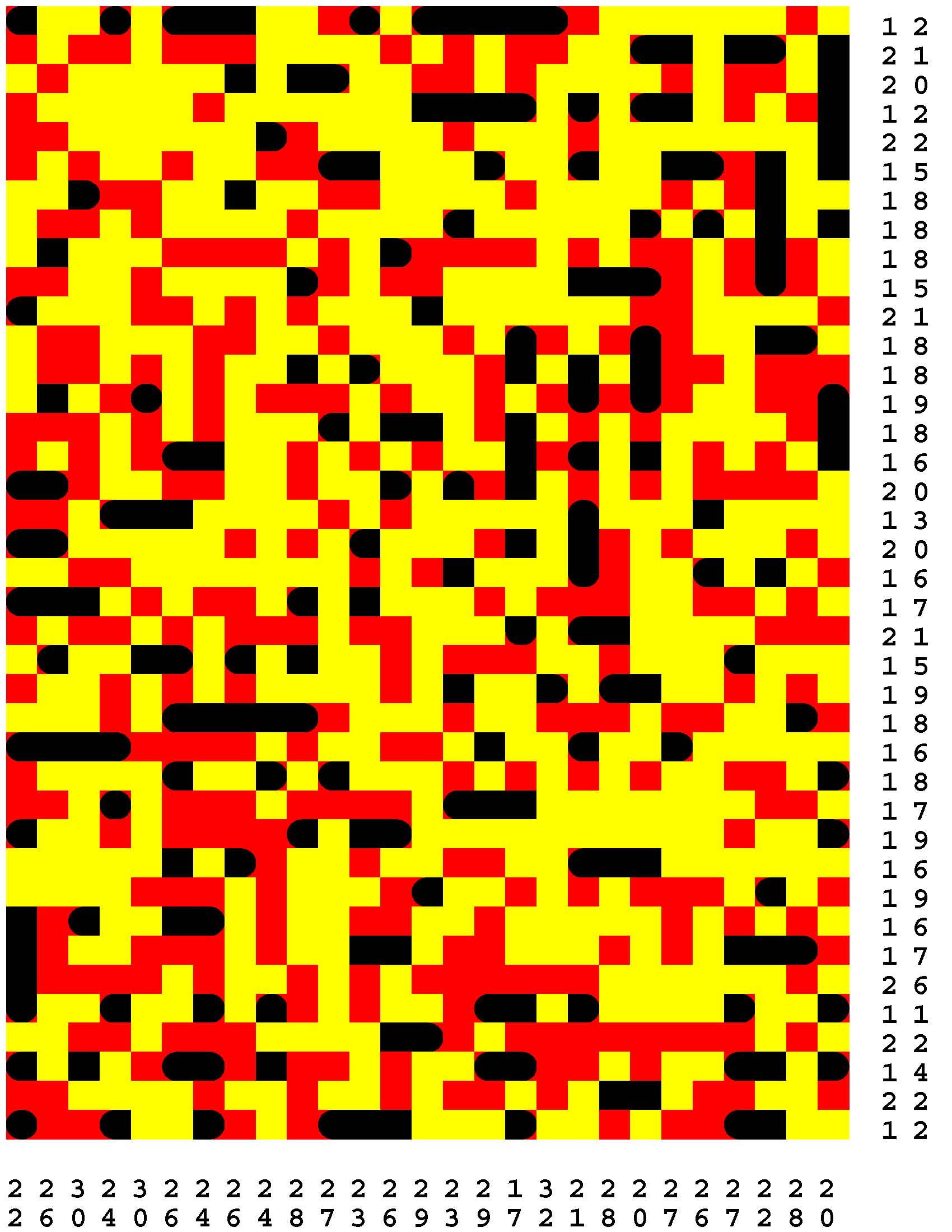
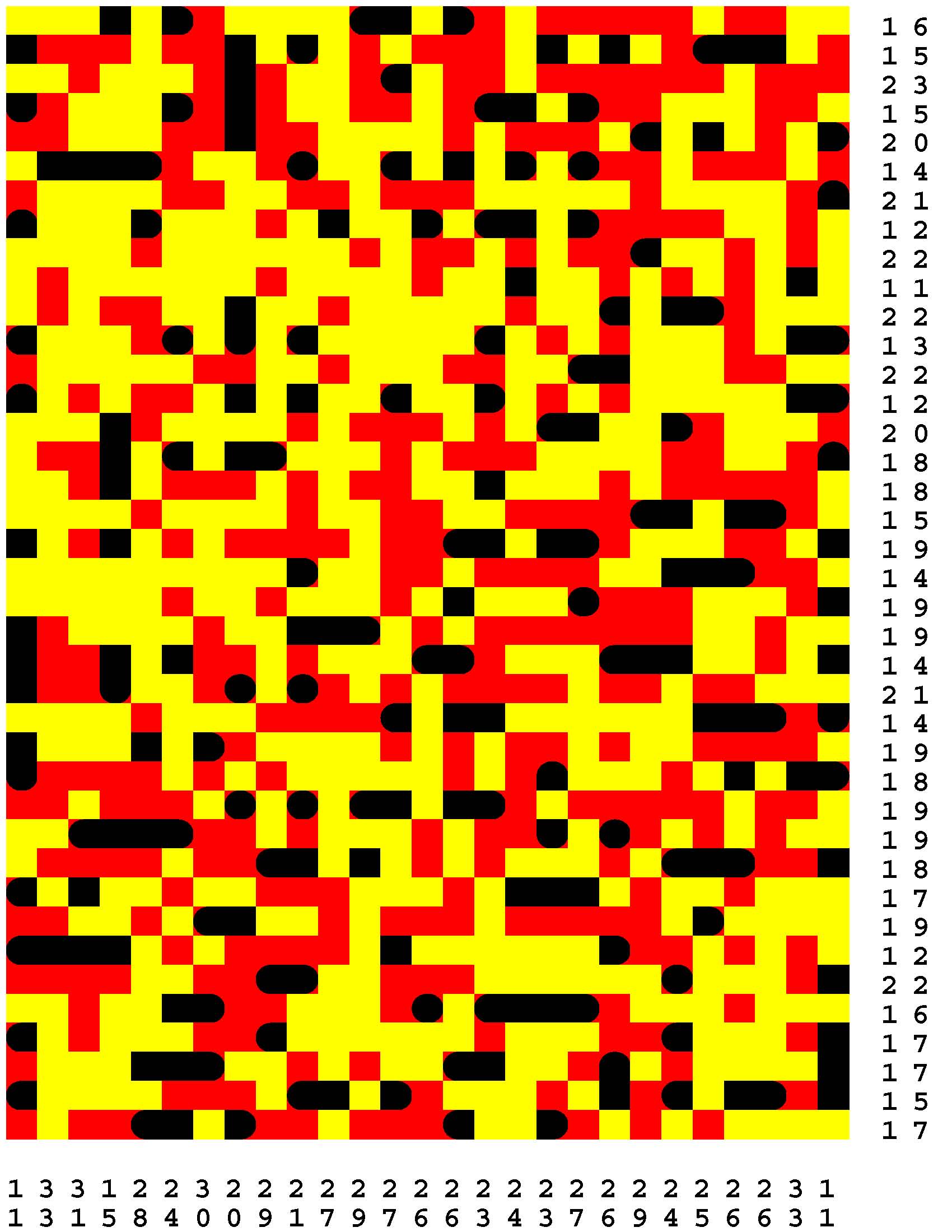
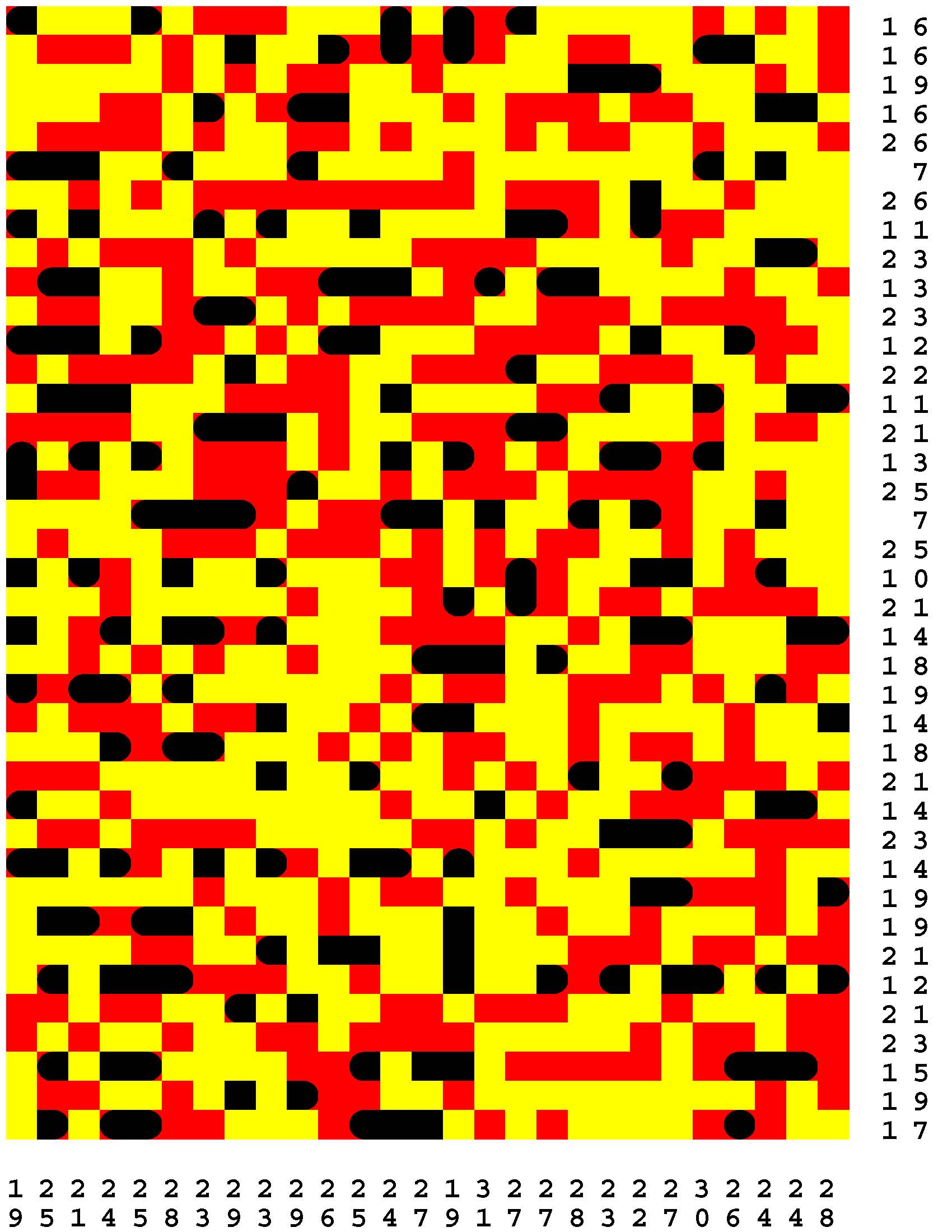
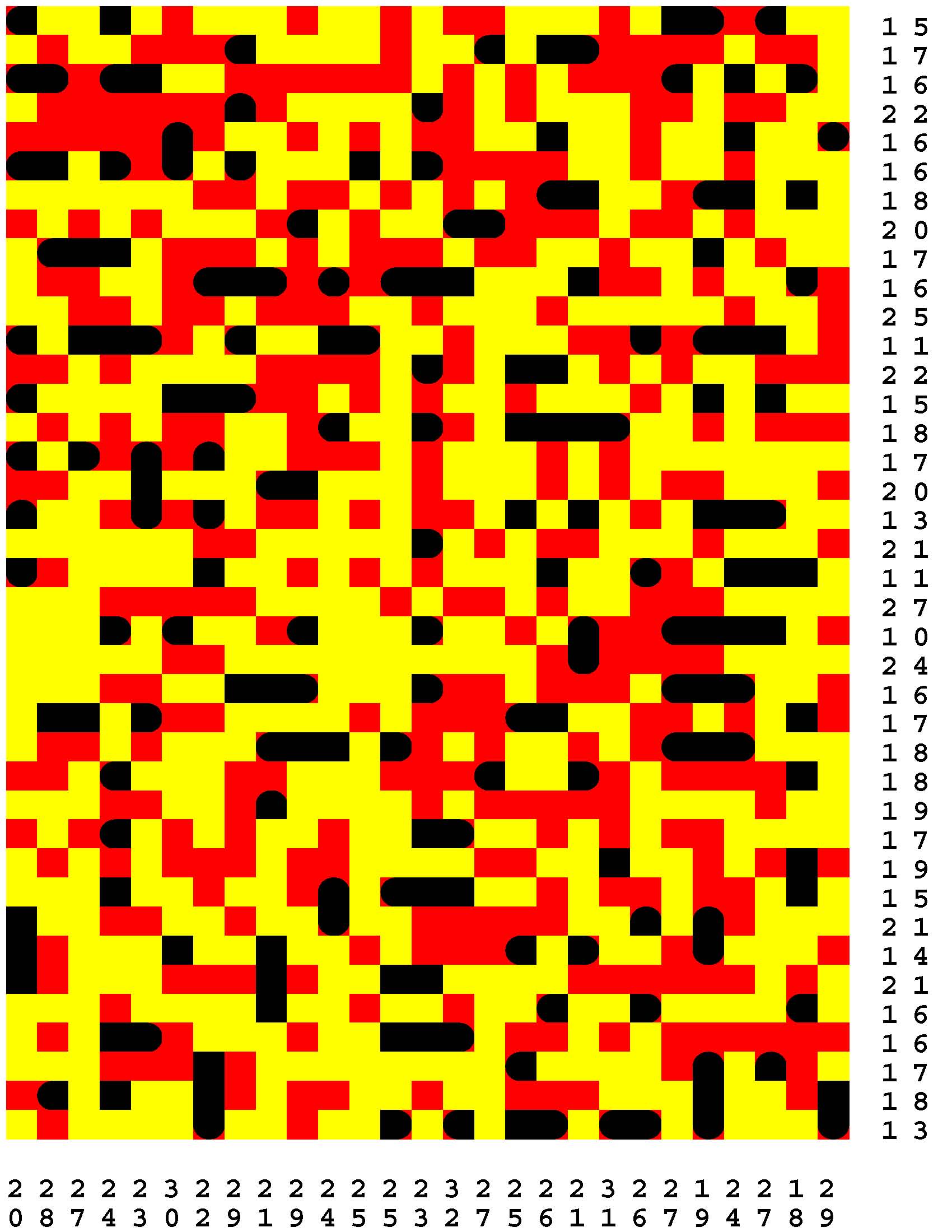
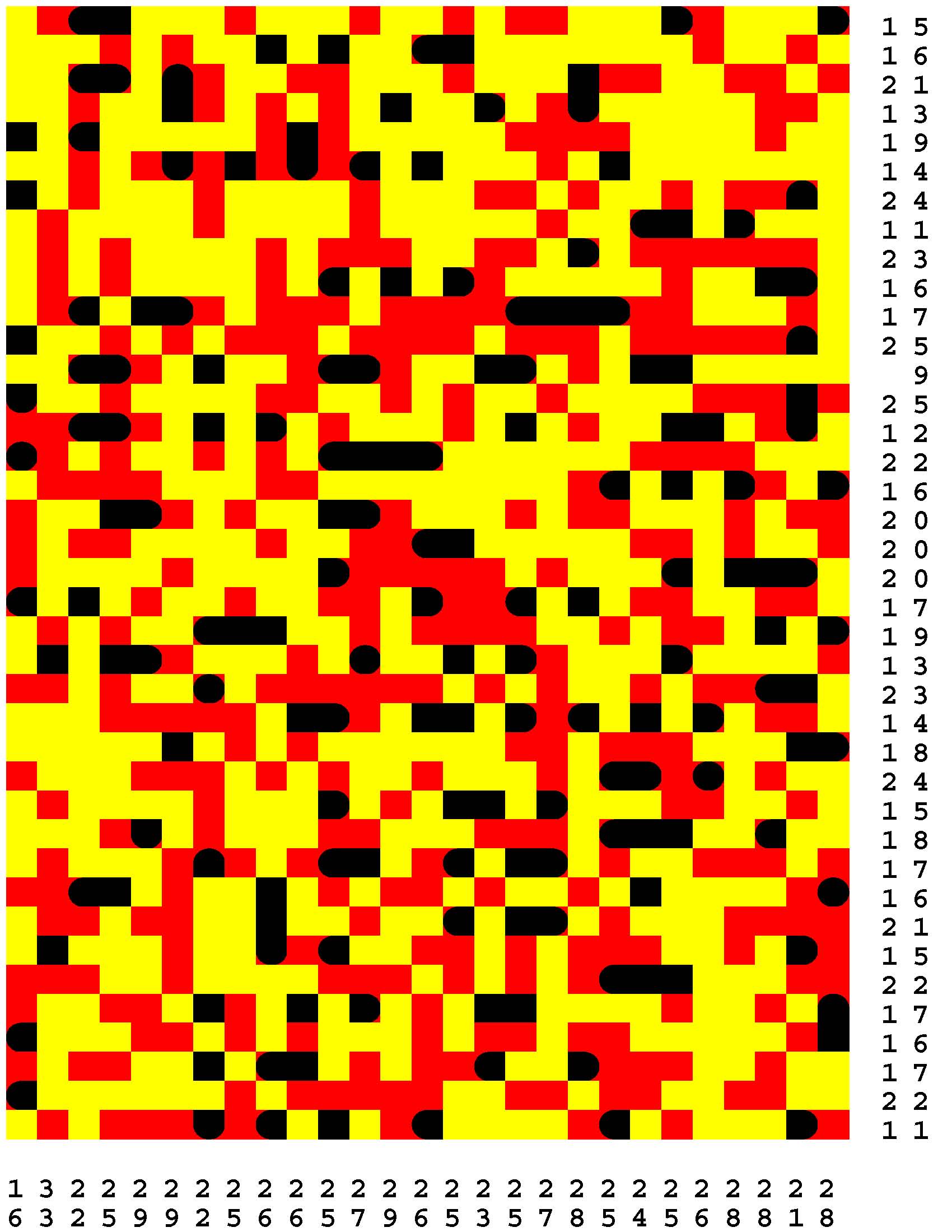
Each Loch Ness Puzzle is an aggrandized restatement of the popular solitaire version of the classic paper-and-pencil game of Battleships.
Each rectangular Loch Ness Puzzle grid represents a fleeting sonar image of the presence or not of the marine life - fabled and otherwise - native to Loch Ness in northwest Scotland. The numerous unremarkable aquatic inhabitants consist of any number of specifically fish specimens anywhere from one to five grid-cells in length. On the other hand, the Loch Ness Monsters, while they are so few in number that they effortlessly make themselves scarce, are individually each more substantial than any one of the fish found there. The Loch Ness Monsters are up to an astounding dozen grid-cells in length and more! Be aware that the diverse menagerie of Loch Ness dwellers may be oriented either horizontally or vertically. |
Moreover, no two inhabitants of Loch Ness can occupy the same nor adjacent grid-cells, not even diagonally i.e. catercornered.
Furthermore, the digit or digits along two of the four sides of each grid respectively provide the number of grid-cells in the corresponding row or column, as the case may be, that DO NOT indicate the presence of a fish or a Loch Ness Monster. Finally, the cumulative graphical results after some fifty percent of the possible probes have been exercised are shown to you right off the bat to start you off in good stead already halfway to your finish line. These gratis revelations may alternatively disclose nothingness (indicated in gray). Or the presence of a single-cell guppy (a black circle). Or the presence of a head or tail of a fish or monster (a black, rounded-off square). Or the presence of a midsection of a fish or monster (a black square). |
One of the compelling challenges is for you to find every instance of the aquatic wildlife in as few additional probes - of your own volition - as possible.
But the overarching goal is to find the longest Loch Ness Monster in each book of a total of 294 Loch Ness Puzzles. Each book consists of forty-two 39x27-cell Loch Ness Puzzles. Plus forty-two additional 46x32-cell Loch Ness Puzzles. Plus forty-two additional 53x37-cell Loch Ness Puzzles. Plus forty-two additional 60x42-cell Loch Ness Puzzles. Plus forty-two additional 67x47-cell Loch Ness Puzzles. Plus forty-two additional 74x52-cell Loch Ness Puzzles. Plus forty-two additional 80x57-cell Loch Ness Puzzles. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
293,706 Black Diamond Puzzles by Francis Gurtowski
|
This is yet another serious, serious series of books created by Francis Gurtowski.
The prolific author is an authentic, ancient coder, going all the way back to IBM Poughkeepsie (Building 705, no less, second floor) and the heyday of OS/360, Robert Rex Seeber Jr. and the horizontal-microcoded System/360 Model 50, coding pads and the coding-pad veto, punch cards and keypunch machines, and self-modifying code. |
Francis Gurtowski is also a self-styled Henry Ford of contemporary, do-it-yourself, print-on-demand, book publishing.
Henry Ford is synonymous with the assembly line, a perfected process for swiftly turning out a series of ingenious, finished products in a foolproof, mechanically-efficient manner. All 999 of these sequels take full advantage of (Amazon) Kindle Direct Publishing's twin, generous, upper limits of 590 bound-and-paperbacked, 8.5x11-inch pages. |
Given a 7-row by 5-column grid prefilled with a total of 35 arbitrary integers, arrange 0, 1, 2, ... 139 in a 14-row by 10-column second grid such that the sum of the four numbers which you placed in each spatially corresponding composition of four cells in the 14x10 grid matches the value given in the 7x5 grid.
Given a 14-row by 10-column grid prefilled with a total of 140 arbitrary integers, arrange 0, 1, 2, ... 559 in a 28-row by 20-column second grid such that the sum of the four numbers which you placed in each spatially corresponding composition of four cells in the 28x20 grid matches the value given in the 14x10 grid. |
Given a 28-row by 20-column grid prefilled with a total of 560 arbitrary integers, arrange 0, 1, 2, ... 2,239 in a 56-row by 40-column second grid such that the sum of the four numbers which you placed in each spatially corresponding composition of four cells in the 56x40 grid matches the value given in the 28x20 grid.
Each of the 294 puzzles in each of the 999 books in this audacious series created by Francis Gurtowski is a separate entity. |

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
293,706 Super 52-Skiddoo Puzzles by Francis Gurtowski
|
This is yet another serious, serious series of books created by Francis Gurtowski.
The prolific author is an authentic, ancient coder, going all the way back to IBM Poughkeepsie (Building 705, no less, second floor) and the heyday of OS/360, Robert Rex Seeber Jr. and the horizontal-microcoded System/360 Model 50, coding pads and the coding-pad veto, punch cards and keypunch machines, and self-modifying code. |
Francis Gurtowski is also a self-styled Henry Ford of contemporary, do-it-yourself, print-on-demand, book publishing.
Henry Ford is synonymous with the assembly line, a perfected process for swiftly turning out a series of ingenious, finished products in a foolproof, mechanically-efficient manner. All 999 of these sequels take full advantage of (Amazon) Kindle Direct Publishing's twin, generous, upper limits of 590 bound-and-paperbacked, 8.5x11-inch pages. |
Spell 26 hidden words: separate substance from obfuscation.
There is one place for each letter of the alphabet in the twenty-six empty positions of each of the two redacted columns of each of the 294 puzzles in each of the 999 books in this audacious series created by Francis Gurtowski. Each puzzle is a separate entity. |
Fill in each pair of missing letters so that a word is formed reading backwards, not forwards.
There is chaff along with the five-or-more-letter word on each 25-position row. Not all of the letters to the left of the first empty position are used to spell out the pertinent word. Ditto for the letters to the right of the second empty. |

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
Dots & Boxes Endgames by Francis Gurtowski
|
This is yet another serious, serious series of books created by Francis Gurtowski.
The prolific author is an authentic, ancient coder, going all the way back to IBM Poughkeepsie (Building 705, no less, second floor) and the heyday of OS/360, Robert Rex Seeber Jr. and the horizontal-microcoded System/360 Model 50, coding pads and the coding-pad veto, punch cards and keypunch machines, and self-modifying code. Francis Gurtowski is also a self-styled Henry Ford of contemporary, do-it-yourself, print-on-demand, book publishing. Henry Ford is synonymous with the assembly line, a perfected process for swiftly turning out a series of ingenious, finished products in a foolproof, mechanically-efficient manner. This wide-ranging series of fourteen grid-packed workbooks revives dormant childhood enthusiasms for the absorbing dots-and-boxes game. All fourteen of these sequels take full advantage of (Amazon) Kindle Direct Publishing's twin, generous, upper limits of 590 bound-and-paperbacked, 8.5x11-inch pages. These massive collections of lattices enable jaundiced former players like you and me to skip the increasingly onerous foreplay of the challenging leisure-time activity and immediately cut to the chase. |
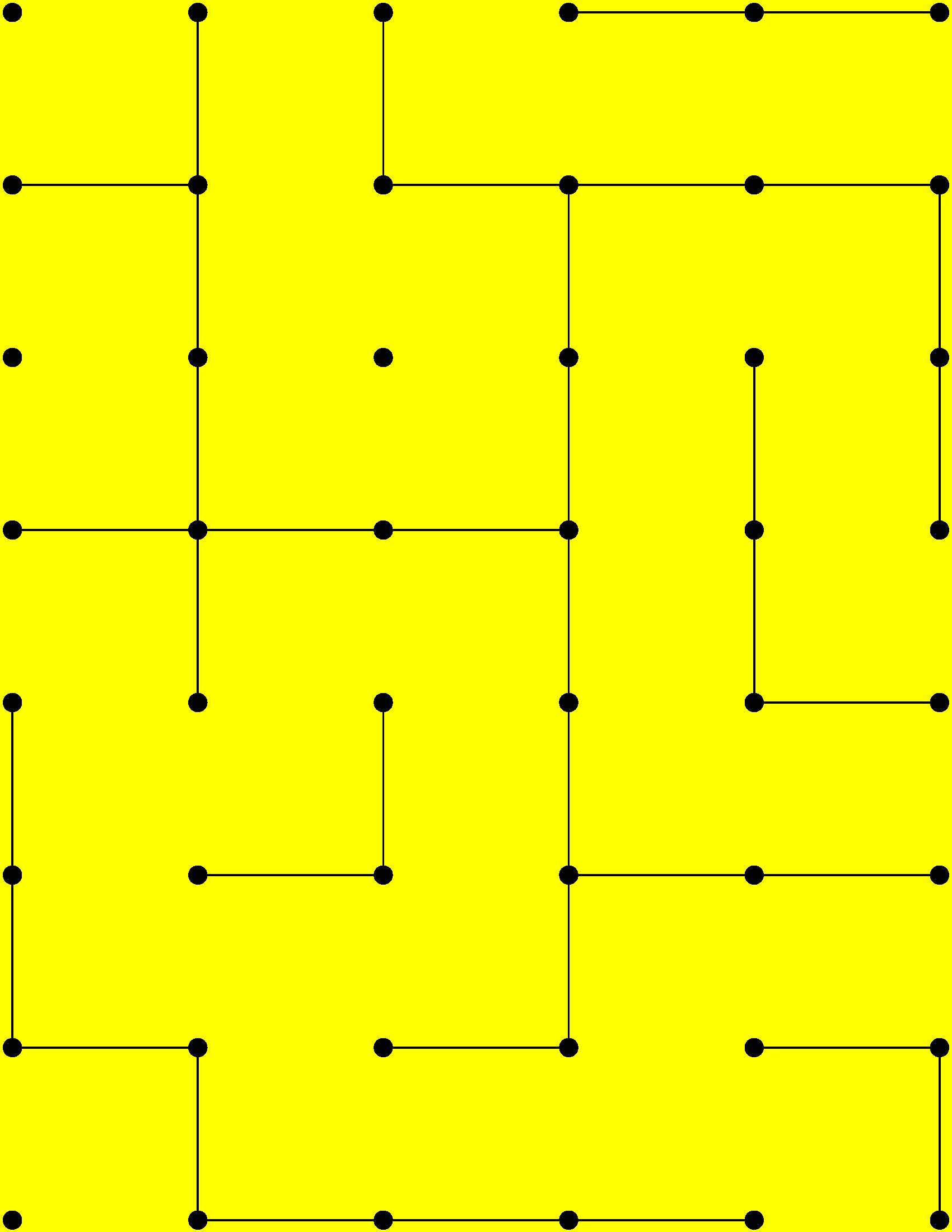
These revolutionary, one-time pads consist of the most cogent dots-and-boxes, ready-made configurations.
Each bound volume in the sequence in turn contains more and more complicated - and more and more carefully calculated by way of my number-crunching algorithm - partially stroked dots-and-boxes setups. Each setup has been set up for you to complete wherein each of the constituent interstices has been teed up but not quite boxed in. It took a lot of code for me to accomplish this amazing hack. But I was determined to create this time-saving literary staircase. I have grown to loathe mindlessly hand-plotting myriad dots in the same old pattern for what seemed like the millionth time. I furthermore found myself abhorring the tedious stroke-by-stroke buildup to the commencement of the gist of the dots-and-boxes game. The more rows and columns a dots-and-boxes grid has the better, I suppose. But the nasty corollary to that hasty assertion is that grid growth becomes more and more of a impediment when laying out the vertices dot-by-dot by hand. |
While there are online sources of preprinted/print-yourself dots-and-boxes templates, those unimaginative bare-bones rote dot patterns pale in comparison to the value-added lattices in this book series which consists of instant dots-and-boxes situations analogous to Laszlo Polgar's classic book of chess endgame problems.
Chess, on the one hand, and dots-and-boxes, on the other, have comparable long-drawn-out opening sequences which only eventually climax in comparable "check states." Unfortunately, over time both over-studied prelims have calcified into timeworn call-and-response rituals akin to military cadences. Of course, "check" is the state in which a chess king is exposed to attack from which the premier chess piece must be protected or moved to safety. The dots-and-boxes sense of that phenomenon arises whenever the very next stroke wherever will tee up the next player to box in an interstice or even a chain of them. Discover the startling aesthetics of the selectively-stroked patterns that emerge as book by book in this series the densities of the underlying infrastructure increase in leaps and bounds. |
As gamers go, we aficionados of the "dots-and-boxes game" are remarkably flexible.
Unlike chess/checkers players or Scrabble players, who are invested in standard grid dimensions e.g. 8x8, 15x15. The precise number of rows of boxes forming the box-game grid does not matter to us. Although, the more the better. Nor the precise number of columns of boxes. Ditto. We only insist that the boxes be squares. During the preparation of this book series I have consequently so far limited myself to a certain ratio of rows to columns. The "golden ratio" in this case happens to be 7/5 or 1.4. 7x5, 14x10, 21x15, 28x20, 35x25, 42x30, 49x35, 56x40, 63x45, 70x50, 77x55, 84x60, 91x65, and 98x70. The respective edge lengths range from 1.5 to 0.1071143 inches. Prepare to sharpen your pencils! |
|

|

|
|||

|

|

|
|||

|

|

|
|||

|

|

|
|||

|

|
||||
293,706 Oxeye Prepper Puzzles by Francis Gurtowski
|
This is a serious, serious series of 999 books.
Each sequel has 590 bound-and-paperbacked pages
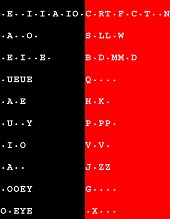
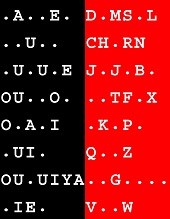
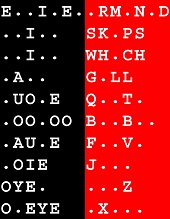
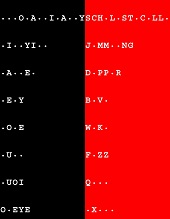
Each puzzle is a stack of 6-14 words 4-15 letters long. The nub and the rub of it? You have to complete the 6-14 riddles.
Each word has 1-6 distinct vowels (i.e. AEIOU and Y).
The vowels are laid out in their precise order of succession.
Every consonant is used somewhere in each puzzle. The 20 consonants & the 6-14 words correspond many-to-one.
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Oxeye Prepper Puzzles is pleasant peacetime playtime pastime family entertainment.
Oxeye Prepper Puzzles is also a clinical antidote to bunker boredom.
Thus the prepper appellation, as in emergency preparedness.
Each volume weighs in at some four pounds apiece.
This prodigious weightiness will serve you well when push comes to shove.
Oxeye Prepper Puzzles will come in handy for self-defense as well as for bartering.

|

|

|

|

|

|
|

|

|

|

|

|

|
|

|

|
|

|

|

|

|

|
|

|
Anatomy of the first ten Oxeye Prepper Puzzles
| Oxeye | Riddle 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | A C C O M P A N Y | S A W F L Y | H U E D | V A R I E T Y | K E B O B | A Q U A | J A Z Z | O G E E | O X E Y E | ||
A . . O . . A . Y | . A . . . Y | . U E . | . A . I E . Y | . E . O . | A . U A | . A . . | O . E E | O . E Y E | |||
. C C . M P . N . | S . W F L . | H . . D | V . R . . T . | K . B . B | . Q . . | J . Z Z | . G . . | . X . . . | |||
C M P N | S W F L | H D | V R T | K B | Q | J Z | G | X | |||
4 | 4 | 2 | 3 | 2 | 1 | 2 | 1 | 1 | |||
| 2 | E U K A R Y O T E | M A D C A P | L U L L | B U N G | F E E S | H I V E | A W A Y | J A Z Z | Q U O I | O X E Y E | |
E U . A . Y O . E | . A . . A . | . U . . | . U . . | . E E . | . I . E | A . A Y | . A . . | . U O I | O . E Y E | ||
. . K . R . . T . | M . D C . P | L . L L | B . N G | F . . S | H . V . | . W . . | J . Z Z | Q . . . | . X . . . | ||
K R T | M D C P | L | B N G | F S | H V | W | J Z | Q | X | ||
3 | 4 | 1 | 3 | 2 | 2 | 1 | 2 | 1 | 1 | ||
| 3 | D E C O R T I C A T I N G | H I S S | F L O E | A W O K E | O B O E | E P O P E E | J I V E | M O U E | Q U E U E | O O Z Y | O X E Y E |
. E . O . . I . A . I . . | . I . . | . . O E | A . O . E | O . O E | E . O . E E | . I . E | . O U E | . U E U E | O O . Y | O . E Y E | |
D . C . R T . C . T . N G | H . S S | F L . . | . W . K . | . B . . | . P . P . . | J . V . | M . . . | Q . . . . | . . Z . | . X . . . | |
D C R T N G | H S | F L | W K | B | P | J V | M | Q | Z | X | |
6 | 2 | 2 | 2 | 1 | 1 | 2 | 1 | 1 | 1 | 1 | |
| 4 | E Q U A T I N G | I M P A I R E R S | D O Z I L Y | C H I V V Y | K A Y A K | O B O E | W A X Y | F I F E | J U J U | ||
E . U A . I . . | I . . A I . E . . | . O . I . Y | . . I . . Y | . A Y A . | O . O E | . A . Y | . I . E | . U . U | |||
. Q . . T . N G | . M P . . R . R S | D . Z . L . | C H . V V . | K . . . K | . B . . | W . X . | F . F . | J . J . | |||
Q T N G | M P R S | D Z L | C H V | K | B | W X | F | J | |||
4 | 4 | 3 | 3 | 1 | 1 | 2 | 1 | 1 | |||
| 5 | A N E S T H E T I C A L L Y | O X I D I Z E D | B O Y A R | M O P E | W I G W A G | J O K E | Q U O I | I F F Y | V I V O | ||
A . E . . . E . I . A . . Y | O . I . I . E . | . O Y A . | . O . E | . I . . A . | . O . E | . U O I | I . . Y | . I . O | |||
. N . S T H . T . C . L L . | . X . D . Z . D | B . . . R | M . P . | W . G W . G | J . K . | Q . . . | . F F . | V . V . | |||
N S T H C L | X D Z | B R | M P | W G | J K | Q | F | V | |||
6 | 3 | 2 | 2 | 2 | 2 | 1 | 1 | 1 | |||
| 6 | G R U B B I N E S S | V O L E | D U C A T | H I P P O | F I F E | M A M M Y | Q U I Z | W A X Y | K A Y O | J U J U | |
. . U . . I . E . . | . O . E | . U . A . | . I . . O | . I . E | . A . . Y | . U I . | . A . Y | . A Y O | . U . U | ||
G R . B B . N . S S | V . L . | D . C . T | H . P P . | F . F . | M . M M . | Q . . Z | W . X . | K . . . | J . J . | ||
G R B N S | V L | D C T | H P | F | M | Q Z | W X | K | J | ||
5 | 2 | 3 | 2 | 1 | 1 | 2 | 2 | 1 | 1 | ||
| 7 | C A N T O N S | A F A R | H O O K U P | J U M B O | G O L L Y W O G | A I D E | V I V O | O Y E Z | Q U O I | O X E Y E | |
. A . . O . . | A . A . | . O O . U . | . U . . O | . O . . Y . O . | A I . E | . I . O | O Y E . | . U O I | O . E Y E | ||
C . N T . N S | . F . R | H . . K . P | J . M B . | G . L L . W . G | . . D . | V . V . | . . . Z | Q . . . | . X . . . | ||
C N T S | F R | H K P | J M B | G L W | D | V | Z | Q | X | ||
4 | 2 | 3 | 3 | 3 | 1 | 1 | 1 | 1 | 1 | ||
| 8 | A N O M A L O U S N E S S | P R I V A T I V E | E K E D | J U J U | W H E E Z Y | B O B B Y | E X E C | Q U A F F | A G O G | ||
A . O . A . O U . . E . . | . . I . A . I . E | E . E . | . U . U | . . E E . Y | . O . . Y | E . E . | . U A . . | A . O . | |||
. N . M . L . . S N . S S | P R . V . T . V . | . K . D | J . J . | W H . . Z . | B . B B . | . X . C | Q . . F F | . G . G | |||
N M L S | P R V T | K D | J | W H Z | B | X C | Q F | G | |||
4 | 4 | 2 | 1 | 3 | 1 | 2 | 2 | 1 | |||
| 9 | C O L D H E A R T E D | J A G G I N G | P O P S | O O Z E | M O V E | B E A K | Q U O I | W A I F | O X E Y E | ||
. O . . . E A . . E . | . A . . I . . | . O . . | O O . E | . O . E | . E A . | . U O I | . A I . | O . E Y E | |||
C . L D H . . R T . D | J . G G . N G | P . P S | . . Z . | M . V . | B . . K | Q . . . | W . . F | . X . . . | |||
C L D H R T | J G N | P S | Z | M V | B K | Q | W F | X | |||
6 | 3 | 2 | 1 | 2 | 2 | 1 | 2 | 1 | |||
| 10 | T H E F T | L E G G I E R | N U D E N E S S | Z A P P Y | C U B I C | M A M M Y | J O K E Y | A Q U A | V I E W | O X E Y E | |
. . E . . | . E . . I E . | . U . E . E . . | . A . . Y | . U . I . | . A . . Y | . O . E Y | A . U A | . I E . | O . E Y E | ||
T H . F T | L . G G . . R | N . D . N . S S | Z . P P . | C . B . C | M . M M . | J . K . . | . Q . . | V . . W | . X . . . | ||
T H F | L G R | N D S | Z P | C B | M | J K | Q | V W | X | ||
3 | 3 | 3 | 2 | 2 | 1 | 2 | 1 | 2 | 1 |
293,706 Genius Puzzles
Here are those very same, first ten Oxeye Prepper Puzzles
though now they have been adapted to better suit
the special needs of persons diagnosed with high IQ.
C M P N S W F L H D V R T K B Q J Z G X
K R T M D C P L B N G F S H V W J Z Q X
D C R T N G H S F L W K B P J V M Q Z X
Q T N G M P R S D Z L C H V K B W X F J
N S T H C L X D Z B R M P W G J K Q F V
G R B N S V L D C T H P F M Q Z W X K J
C N T S F R H K P J M B G L W D V Z Q X
N M L S P R V T K D J W H Z B X C Q F G
C L D H R T J G N P S Z M V B K Q W F X
T H F L G R N D S Z P C B M J K Q V W X
Each genius puzzle is simply a 20-letter permutation.
You are asked to find the corresponding stack of 6-14 words 4-15 letters long.
Neither an overall schematic nor redacted spellings are given.
Each word has 1-6 distinct vowels (i.e. AEIOU and Y).
Each word has 1-10 distinct consonants too.
Every consonant is used somewhere in each puzzle.
Each consonant is restricted to a single word per puzzle.
20 consonants & 6-14 words correspond many-to-one.
293,706 Homophonic Prepper-Checksums-Puzzles by Francis Gurtowski
|
This is yet another serious, serious series of 999 books created by Francis Gurtowski.
The prolific author is an authentic, ancient coder, going all the way back to IBM Poughkeepsie (Building 705, no less, second floor) and the heyday of OS/360, Robert Rex Seeber Jr. and the horizontal-microcoded System/360 Model 50, coding pads and the coding-pad veto, punch cards and keypunch machines, and self-modifying code.
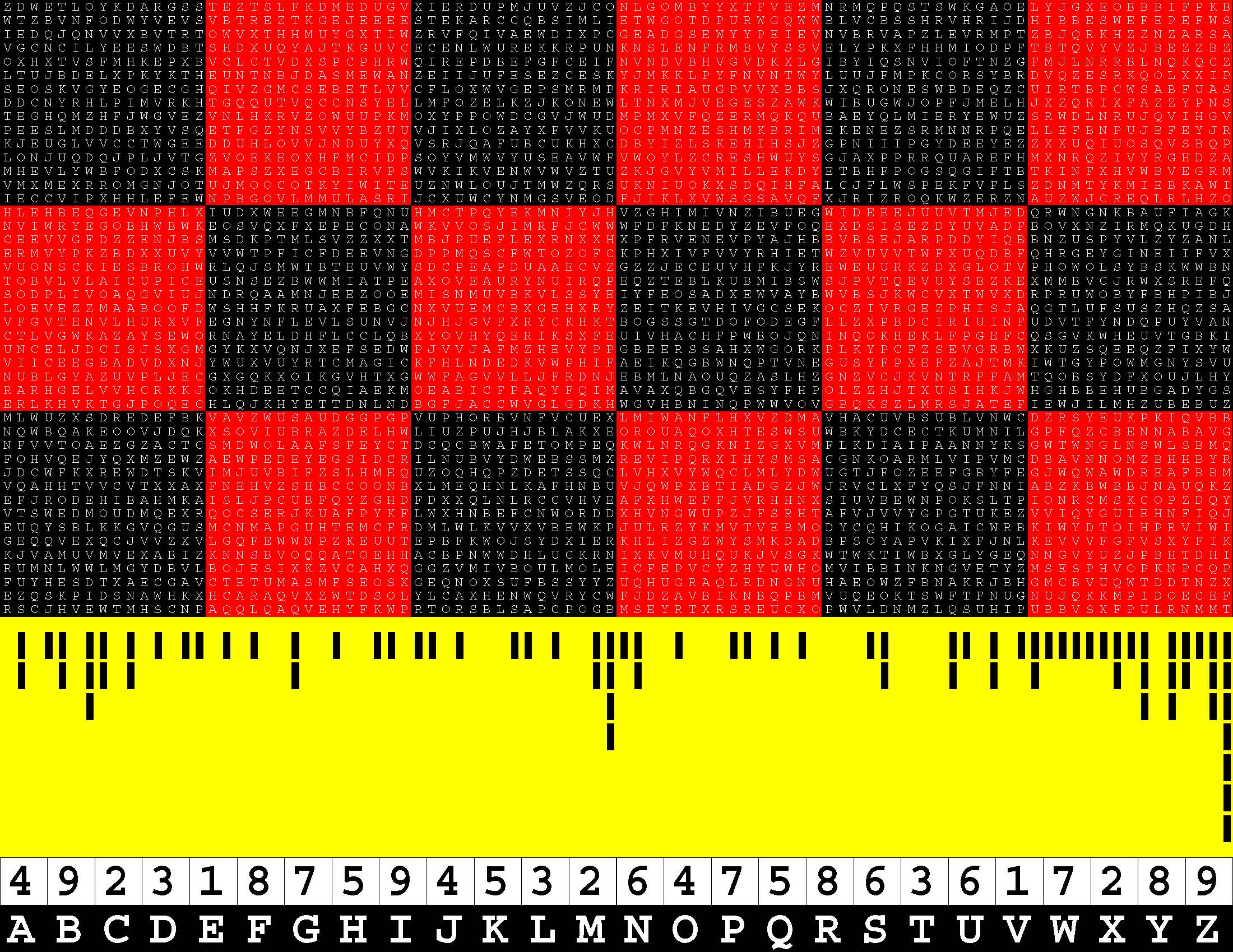
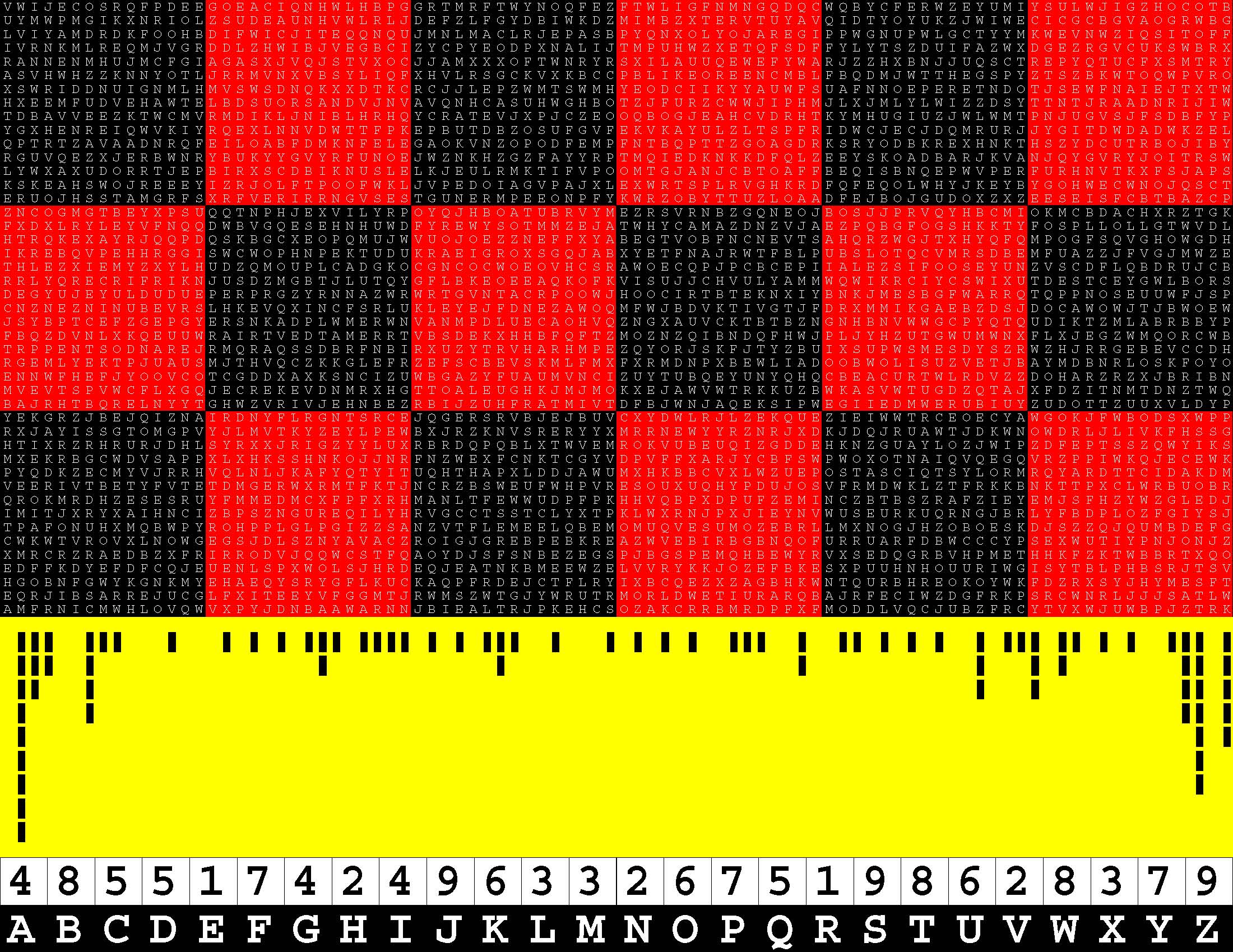
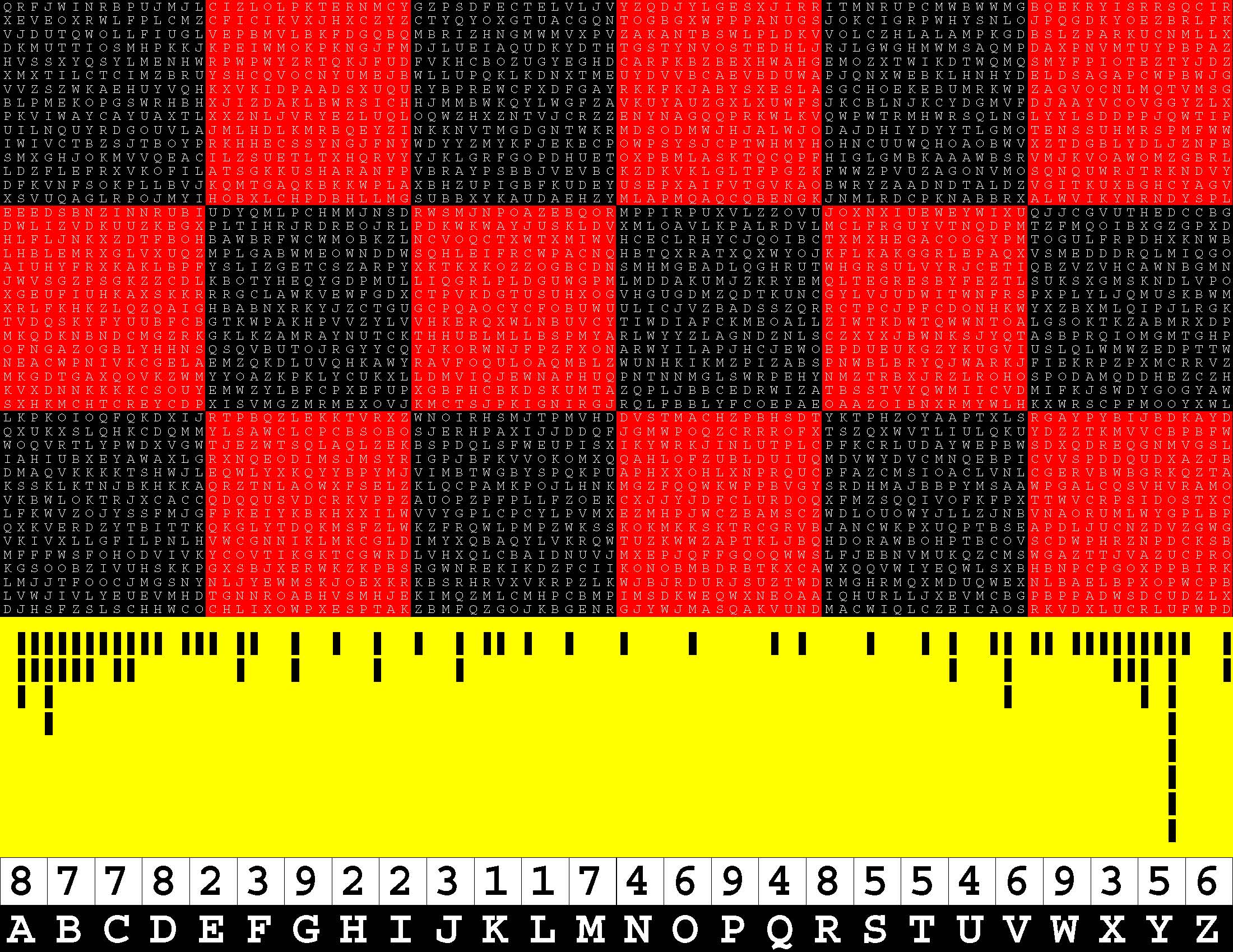
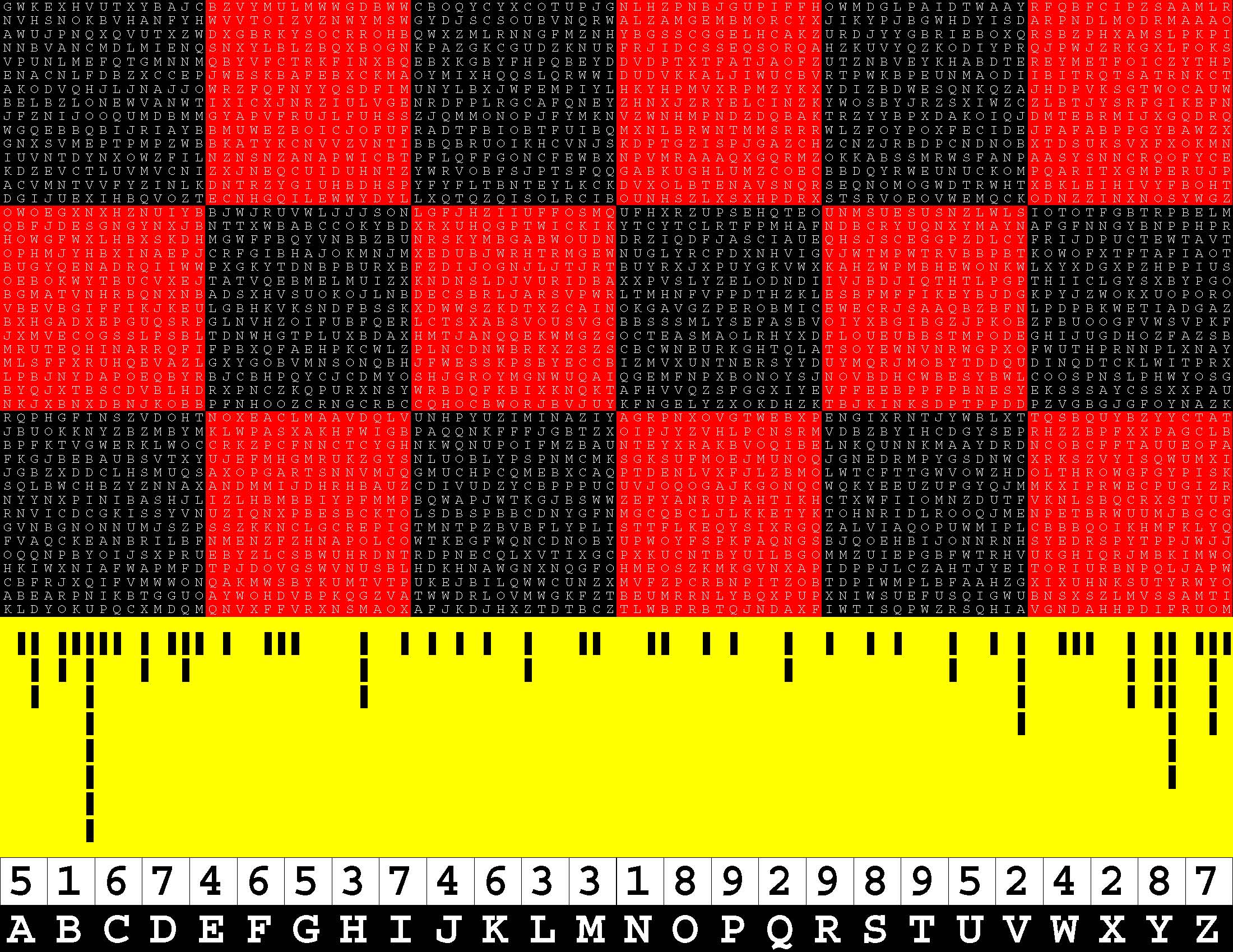
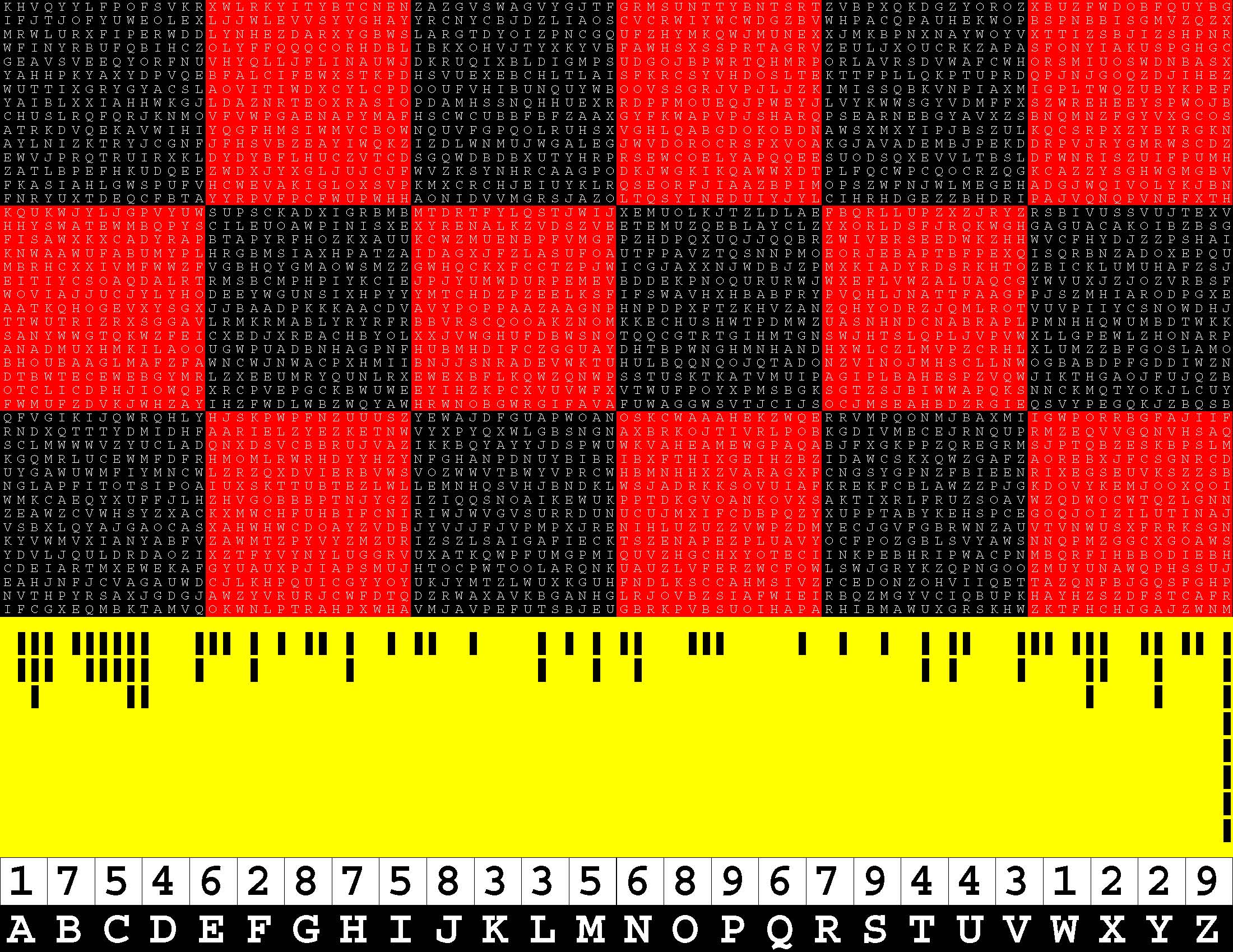
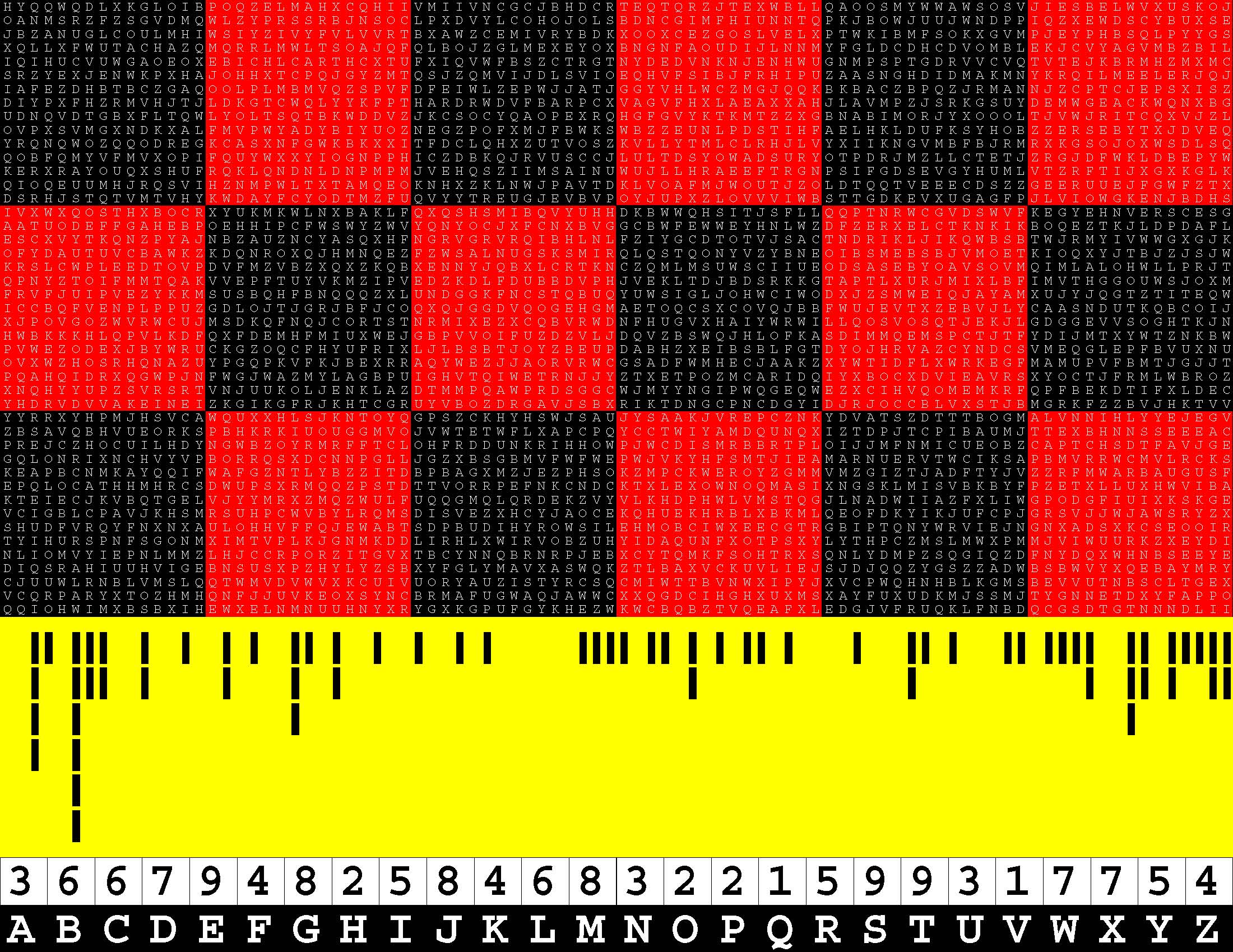
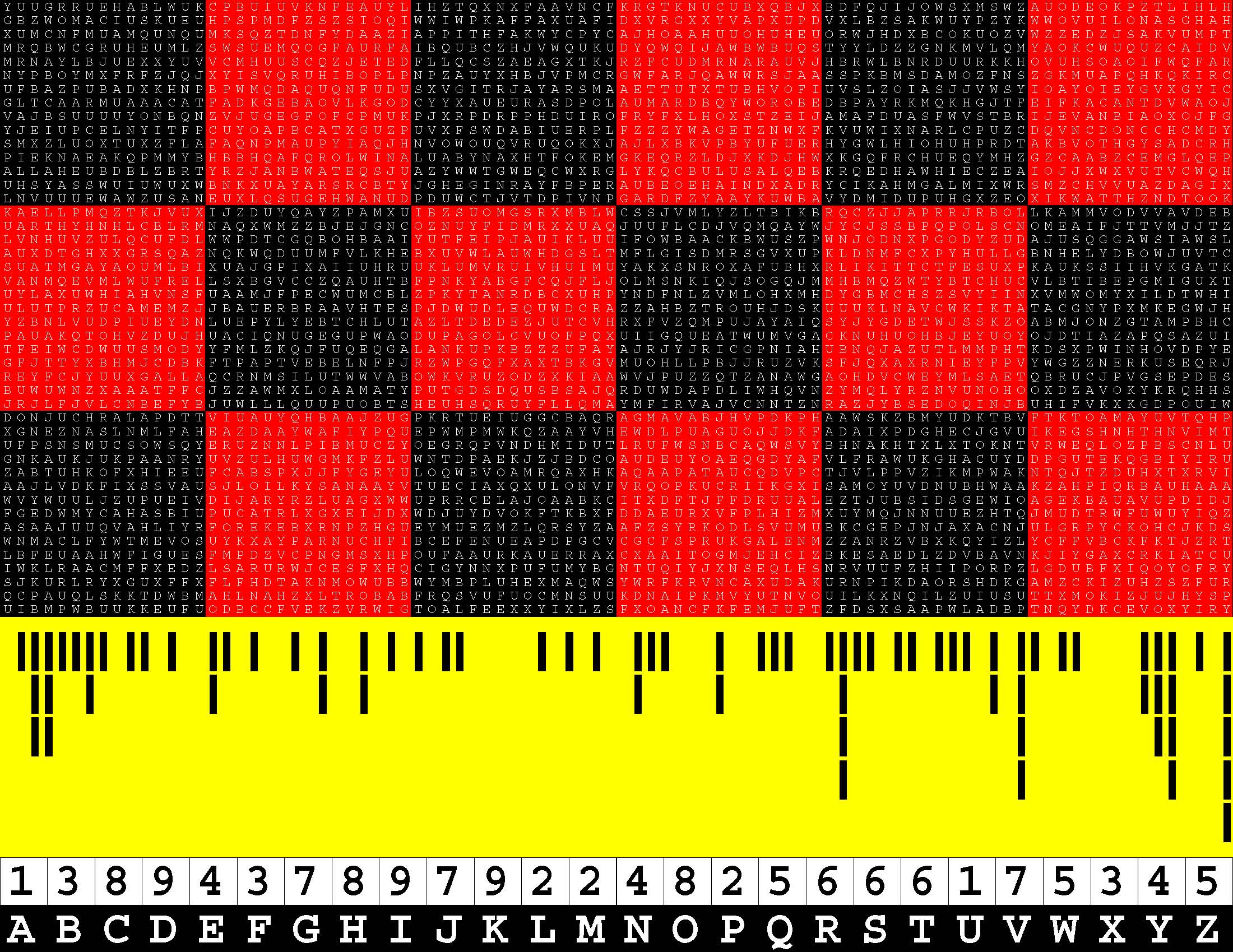
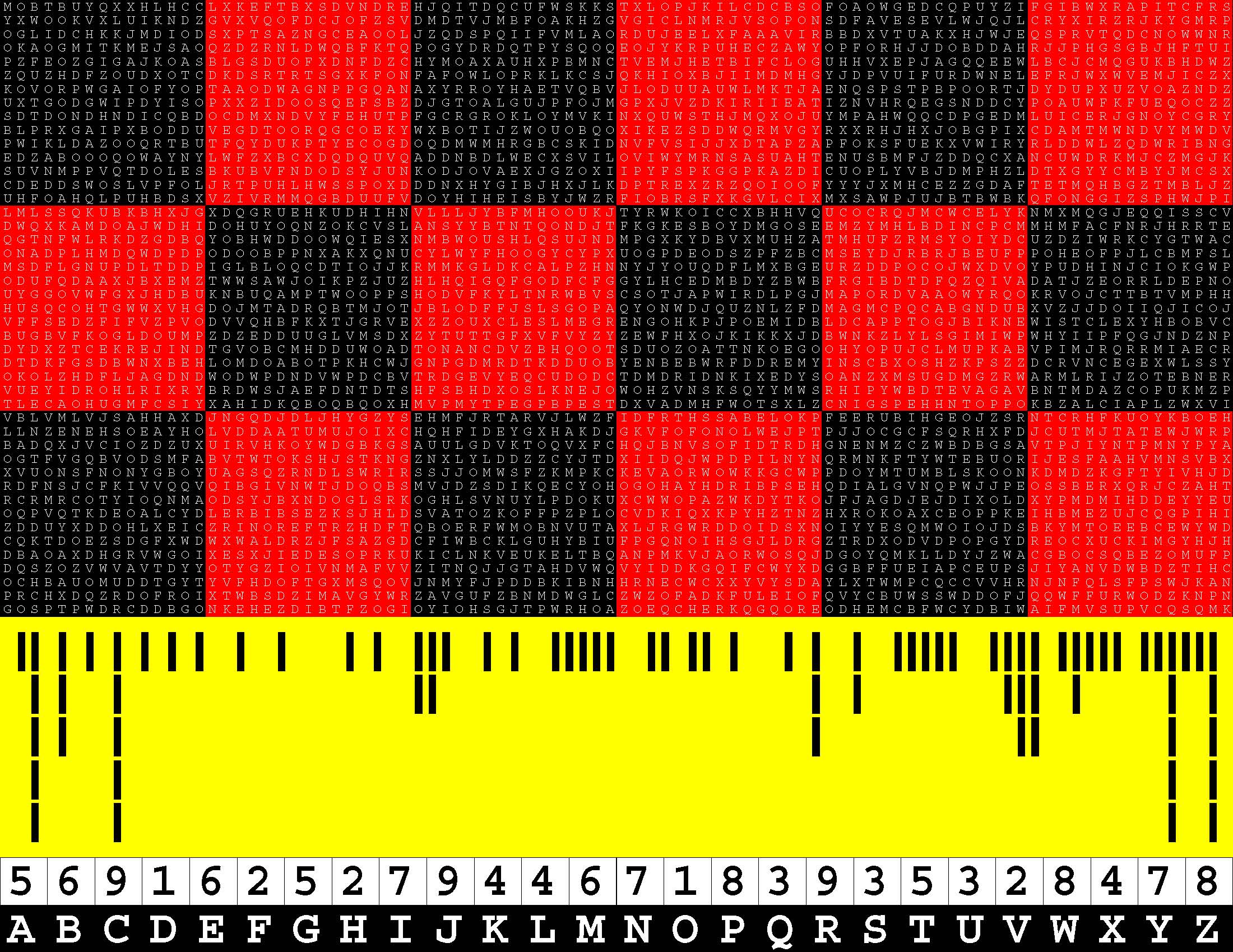
Francis Gurtowski is also a self-styled Henry Ford of contemporary, do-it-yourself, print-on-demand, book publishing. Henry Ford is synonymous with the assembly line, a perfected process for swiftly turning out a series of ingenious, finished products in a foolproof, mechanically-efficient manner. Once again, each of these sequels takes full advantage of (Amazon) Kindle Direct Publishing's twin, generous, upper limits of 590 bound-and-paperbacked, 8.5x11-inch pages. Whereas the book series cited above is packed with 294 two-page, word puzzles, this one is instead chock-full of 147 four-page, letter-substitution specimens of ciphertext-cum-plaintext. The concept is simple enough. Each puzzle consists of a 45x90-letter rectangular block of alphabetic text which you have to translate into a 45x90-digit block of decimal text. Replace each letter A-Z with a digit 1-9. |
The plaintext is by definition homophonically encoded in the ciphertext.
Homophonic? Homophonic refers to the fact that each decimal digit in the plaintext is alternatively represented by more than one ciphertext alphabetical letter. Moreover, this is a uniquely mathematical, letter-substitution, cipher system. Whereas letter-substitution schemes have heretofore have been exclusively non-mathematical in nature. Moreover, the mathematical aspects of the plaintext go far beyond the mere replacement of each letter A-Z in the ciphertext with a decimal digit 1-9 in the plaintext. To begin with, each row of 90 decimal digits must add up to the same sum whatever. Spoiler alert! Regarding the puzzle specimen elucidated below, the common linear checksum just happens to be 449. In theory, given the common linear checksum, it may be possible for you to find A-Z analytically rather than by trial and error. |
The other mathematical constraint is that each of the succeeding columnar sums (i.e. each of the succeeding checksums) must be equal to or greater than (i.e. ≥) its immediate predecessor.
In the books themselves, the required changes (or not) in the sum of the digits in the succeeding columns are designated graphically. Regarding the puzzle specimen elucidated below, the required columnar increments (or not) are instead designated in absolute terms: +2, 0, 1, 2, 0, 3, 2, 0, 2, 0, 1, 0, 1, 1, 0, 1, 0, 1, 0, 0, 2, 0, 0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 0, 2, 4, 1, 2, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 2, 0, 0, 0, 0, 2, 1, 0, 2, 0, 1, 2, 1, 1, 1, 1, 1, 2, 1, 3, 0, 3, 2, 1, 3, and 7. Spoiler alert! The first columnar checksum just happens to be 191. Ergo, the succeeding 89 checksums are: 193, 193, 194, 196, 196, 199, 201, 201, 203, 203, 204, 204, 205, 206, 206, 207, 207, 208, 208, 208, 210, 210, 210, 211, 211, 211, 212, 213, 213, 214, 215, 215, 216, 216, 216, 216, 217, 218, 218, 219, 219, 219, 221, 225, 226, 228, 228, 228, 229, 229, 229, 229, 230, 231, 231, 232, 232, 233, 233, 233, 233, 233, 234, 236, 236, 236, 236, 236, 238, 239, 239, 241, 241, 242, 244, 245, 246, 247, 248, 249, 251, 252, 255, 255, 258, 260, 261, 264, and 271. |
|
|
|
|
|
|
|
|

|
|

|
|

|
|
|
|
|
 /td>
/td>
|

|
|
|
|
|

|
A Specimen Of The Ciphertext
ZDWETLOYKDARGSSTEZTSLFKDMEDUGVXIERDUPMJUVZJCONLGOMBYYXTFVEZMNRMQPQSTSWKGAOELYJGXEOBBBIFPKB WTZBVNFODWYVEVSVBTREZTKGEJEEEESTEKARCCQBSIMLIETWGOTDPURWGQWWBLVCBSSHRVHRIJDHIBBESWEFEPEFWS IEDQJQNVVXBVTRTOWVXTHHMUYGXTIWZRVFQIVAEWDIXPCGEADGSEWYYPEIEVNVBRVAPZLEVRMPTZBJQRKHZZNZARSA VGCNCILYEESWDBTSHDXUQYAJTKGUVCECENLWUREKKRPUNKNSLENFRMBVYSSVELYPKXFHHMIODPFTBTQVYVZJBEZZBZ OXHXTVSFMHKEPXBVCLCTVDXSPCPHRWQIREPDBEFGFCEIFNVNDVBHVGVDKXLGIBYIQSNVIOFTNZGFMJLNRRBLNQKQCZ LTUJBDELXPKYKTHEUNTNBJDASMEWANZEIIJUFESEZCESKYJMKKLPYFNVNTWYLUUJFMPKCORSYBRDVQZESRKQOLXXIP SEOSKVGYEOGECGHQIVZGMCSEBETLVVCFLOXWVGEPSMRMPKRIRIAUGPVVXBBSJXQRONESWBDEQZCUIRTBPCWSABFUAS DDCNYRHLPIMVRKHTGQQUTVQCCNSYELLMFOZELKZJKONEWLTNXMJVEGESZAWKWIBUGWJOPFJMELHJXZQRIXFAZZYPNS TEGHQMZHFJWGVEZVNLHKRVZOWUUPKMOXYPPOWDCGVJWUDMPMXVFQZERMQKQUBAEYQLMIERYEWUZSRWDLNRUJQVIHGV PEESLMDDDBXYVSQETFGZYNSVVYBZUUVJIXLOZAYXFVVKUOCPMNZESHMKBRIMEKENEZSRMNNRPQELLEFBNPUJBFEYJR KJEUGLVVCCTWGEEDDUHLOVVJNDUYXQVSRJQAFUBCUKHXCDBYIZLSKEHIHSJZGPNIIIPGYDEEYEZZXXUQIUOSQVSBQP LONJUQDQJPLJVTGZVOEKEOXHFMCIDPSOYVMWVYUSEAVWFVWOYLZCRESHWUYSGJAXPPRRQUAREFHMXNRQZIVYRGHDZA MHEVLYWBFODXCSKMAPSZXEGCBIRVPSWVKIKVENWVWVZTUZKJGVYVMILLEKDYETBHFPOGSQGIFTBTKINFXHVWBVEGRM VMXMEXRROMGNJOTUJMOOCOTKYIWITEUZNWLOUJTMWZQRSUKNIUOKXSDQIHFALCJFLWSPEKFVFLSZDNMTYKMIEBKAWI IECCVIPXHHLEFEWNPBGOVLMMULASRIJCXUWCYNMGSVEODFJIKLXVWSGSAVQFXJRIZROQKWZERZNAUZWJCREQLRLHZO HLEHBEQGEVNPHLXIUDXWEEGMNBFQNUHMCTPQYEKMNIYJHVZGHIMIVNZIBUEGWIDEEEJUUVTMJEDQRWNGNKBAUFIAGK NVIWRYEGOBHWBWKEOSVQXFXEPECONAWKVVOSJIMRPJCWWWFDFKNEDYZEVFOQEXDSISEZDYUVADFBOVXNZIRMQKUGDH CEEVVGFDZZENJBSMSDKPTMLSVZZXXTMBJPUEFLEXRNXXHXPFRVENEVPYAJHBBVBSEJARPDDYIQBBNZUSPYVLZYZANL ERMVYPKZBDXXUVYVVWTPFICFDEEVNGDPPMQSCFWTOZOFCKPHXIVFVVYRHIETWZVUVVTWFXUQDBFQHRGEYGINEIIFVX VUONSCKIESBROHWRLQJSMWTBTEUVWYSDCPEAPDUAAECVZGZZJECEUVHFKJYREWEUURKZDXGLOTVPHOWOLSYBSKWWBN TOBVLVLAICUPICEUSNSEZBWWMIATPEAXOVEAURYNUIRQPEQZTEBLKUBMIBSWSJPVTQEVUYSBZKEXMMBVCJRWXSREFQ SODPLIVOAQGVIUJNDRQAAMNJEEZOOEMISNMUVBKVLSSYEIYFEOSADXEWVAYBWVBSJKWCVXTWVXDRPRUWOBYFBHPIBJ LOEVEZZMAABOOFDWSHHFKRUAXFEBGCNXVUEMCBXGEHXRYZEITKEVHIVGCSEKOCZIVRGEZPHISJAQGTLUFSUSZHQZSA VFGVTENVLHURXVFEGNYNFLEVLSUNVJNJHJGVFXRYCKHKTBOGSSGTDOFODEGFLLZXPBDCIRIUINFUDVTFYNDQPUYVAN CTLVGWKAZAYSEWORNAYELDHFLCCLQBXYOVHYQERIKSXFEUIVHACHFPWBOJQNINQOKHEKLFPGEFCQSGVKWHEUVTGBKI UNCELJDCISJSXGMGYKXVQNJXEFSEDWPJVVJAFMZHEVYPPGBEERSSAHXWGORKPLKYPCFZSEVGRBWXKUZSQEEQZFIXYW VIICEEGEADVDXNJYWUXVUYRTCMAGICKFHLNDEDKVWPHIFAEIKQGBWNQPTVNEGUSYFPXEFZAJTMKIWTGYPOWMGNYSVU NUBLGYAZUVPLJECGXGQKXOIKGVHTXGWWFAGVVLLJFRDNJEBMLNAOUQZASLHZGNZVCJKVNTRFFAMTQOBSYDFXOUJLHY RARHGELVVHCRKKJOKHDEETCCQIAEKMOEABICFPAQYFQIMAVAXQBGQVESYFHPOLZZHJTXUSIHKJWHGHBBEHUBGADYGS ERLKHVKTGJPOQECHLQJKHYETTDNLNDBGFJACCWVGLGDKHWGVHBNINQPWWVOVGBQKSZLMRSJATEFIEWJILMHZUBEBUZ MLWUZXSDREDEFBKVAVZWUSAUDGGPGPVUPHORBVNFVCUEXLMIWANFLHXVZDMAVHACUVBSUBLVNWCDZRSYEUKPKIQVBB NQWBQAKEOOVJDQKXSOVIUBRAZDELHWLIUZPUJHJBLAKXEOROUAQOXHTESWSUWBKYDCECTKUMNILGPFQZCBENNABAVG NFVVTOAEZGZACTCSMDWOLAAFSFEYCTDCQCBWAFETOMPEQKWLNRQGKNIZGXVMFLKDIAIPAANNYKSGWTWNGLNSWLSBMQ FOHVQEJYQXMZEWZAEWPEDEYEGSIDCRILNUBVYDWEBSSMXREVIPQRXIHYSMSACGNKOARMLVIPVMCDBAVNNOMZBHHBYR JDCWFKXREWDTSKVIMJUVBIFZSLHMEQUZOQHQPZDETSSQCLVHXVYWQCLMLYDWUGTJFOZEEFGBYFEGJWQWAWDREAFBBM VQAHHTVVCVTXXAXFNEHVZSHBCCOONBXLMEQHNLKAFHNBUVJQWPXBTIADGZJWJRVCLXFYQSJFNNIABZKBWBBJNAUQKZ EFJRODEHIBAHMKAISLJPCUBFQYZGHDFDXXQLNLRCCVHVEAFXHWEFFJVRHHNXSIUVBEWNPOKSLTPIONRCMSKCOPZDQY VTSWEDMOUDMQEXRQOCSERJKUAFPYKFLWXHNBEFCNWORDDXHVNGWUPZJFSRHTAFVJVVYGPGTUKEZVVIQYGUIEHNFIQJ EUQYSBLKKGVQGUSMCNMAPGUHTEMCFRDMLWLKVVXVBEWKPJULRZYKMVTVEBMODYCQHIKOGAICWRBKIWYDTOIHPRVIWI GEQQVEXQCJVVZXVLGQFEWWNPZKEUUTEPBFKWOJSYDXIERKHLIZGZWYSMKDADBPSOYAPVKIXFJNLKEVVVFGFVSXYFIK KJVAMUVMVEXABIZKNNSBVOQQATOEHHACBPNWWDHLUCKRNIXKVMUHQUKJVSGKWTWKTIWBXGLYGEQNNGVYUZJPBHTDHI RUMNLWWLMGYDBVLBOJESIXKZVCAHXQGGZVMIVBOULMOLEICFEPVCYZHYUWHOMVIBBINKNGVETYZMSESPHVOPKNPCQP FUYHESDTXAECGAVCTETUMASMFSEOSXGEQNOXSUFBSSYYZUQHUGRAQLRDNGNUHAEOWZFBNAKRJBHGMCBVUQWTDDTNZX EZQSKPIDSNAWHKXHCARAQVXZWTDSOLYLCAXHENWQVRYCWFJDZAVBIKNBQPBMVUQEOKTSWFTFNUGNUJQKKMPIDOECEF RSCJHVEWTMHSCNPAQQLQAQVEHYFKWPRTORSBLSAPCPOGBMSEYRTXRSREUCXOPWVLDNMZLQSUHIPUBBVSXFPULRNMMT +20120320201011010100200100110110100011010024120010001101010000120000210201211111213032137
The Corresponding Specimen Of The Plaintext
937133485348766319363853213671291836724619424637429882381192682575636757441384721499998759 739916843781116193819357141111631548225969239137743376877577931296658158943599916718171876 913545611291383471235526872397981859141739272714376178871911619814793118273994585599694864 172629381167393653265844357612121637681558766566316882918661138752855294378393518194919999 425231682551729123231326727587598173918782198616319517135237998956619483697824368893655529 336493132758535166369434621746919946816192165842553788616378366482752486898315916855432297 614651781471275591972261913311283427171762827589894677112996425846167931592698397276498646 332688537921855375563152266813328491359454617336224117169475799677447842135429589284998766 317552958477119163558194766752428774732714763272218591825556941853291881769687336864519571 711632333928165138798661189966149234948281156427269165259892151619682668751331896764981848 541673112237711336534114636825168454869265522398993651595649776999778311819922659646516957 346465354734137914151425822937648127186614178174839281657686744277885648185226859918875394 251138798432265247692172998176715951167171936954718129331538139587476579839359682517911782 122212884276443642442435897931696734643279586656964526359584324837671581836936238529195479 912219725531817679741322634689422672862761143849532176764158248998455791896469742815383594 531591571167532963271172698566522375815269845197592916999617793111466132413587676594689475 619788174957975146152821712464751146492874277783856138911845123696193861438941269982556735 211117839916496263573236199223294761831286225278811611784459919614487338959969667813989463 182187599322618117378928311167377256287349482575291811885913791611378265398558718796199812 164662591698457835462739316178632714736441219799412161585488171668593273431754743689657796 349131349267921666619977294371424114688669857159319356929967647135116869951222912487268185 643739144571964638544264119441296626195136681988146432171489719645721237123878674988957994 341119924494483765585864281972621612292715288919351159172615429918719759644573368666955964 187131613568218176868311366614645471828825553947667334843178339279329896968631388635768146 233177549486174864813358322359284158518956281691542587794456965455153877182567157516137959 662134329646272785215642186137741144829511877791186645277485735872896117897256965115989287 199211714313264876216883224792585363135177598419557976573161766887218944325973787472768616 669378496173412727552495715327778471133488364192364465946359769124516388842354968382464358 848571311528554455311322594152414992874588592414259751168857439954326695547575991569743876 183551537474512535455813336363978442271737355771596965777141795569328644318917493259691969 237692638131895141976646377777167548916812612329746835219324154261966931672398681657595199 657954514414355264196984931357396976454934521484645425316766795832123562693778592916649417 681134419794232623743448681823325297481342715573685756997212835394974466856773767366736925 845151485229179417713181769328936691837196622811975829586264276544823197122394166429955988 432785281733651924619989635215694555793136652315218752323837673484911879881747574738148992 154553112132242861519659224469232155635485696145772939437947481232885648669499597994646559 184843159945254963472698589753832253638221511482571884185562696191767456337946822652479358 136713246325128542618456487858372569182674833251677679486853481411877736519119587691568954 165869355715766226247765312288323735112191757463898521311924382559547492789597833495781979 715511252411921375817767951663179857446832918553997978625343976484715928463511118781628895 541426121124999566691455434155429767735362586925126556541675737539792738715667186947953359 862637732783913944169259124525779129194632431928171289586754219999656711389261675147567257 868516332412741231362462861462715642668966889655678453836766541479896458495722916573333692 195657936647552524845129733643832425167518827843941995695792165145367838667664555279341218 862451173256267455354511588577834869364727479261883286816224771336293566597699162876386223 +20120320201011010100200100110110100011010024120010001101010000120000210201211111213032137
The Corresponding
System of 135 Simultaneous Linear Equations
With 26 Unknowns A-Z
2A+ 5B+ 1C+ 5D+ 7E+ 3F+ 5G + 2I+ 3J+ 4K+ 4L+ 5M+ 2N+ 5O+ 3P+ 2Q+ 3R+ 5S+ 5T+ 3U+ 3V+ 2W+ 3X+ 4Y+ 4Z=449
1A+ 7B+ 3C+ 3D+13E+ 3F+ 3G+ 3H+ 4I+ 2J+ 2K+ 2L+ 1M+ 1N+ 2O+ 2P+ 2Q+ 5R+ 7S+ 6T+ 1U+ 6V+ 8W + 1Y+ 2Z=449
5A+ 3B+ 1C+ 3D+ 7E+ 1F+ 3G+ 3H+ 5I+ 2J+ 1K+ 1L+ 2M+ 3N+ 1O+ 4P+ 4Q+ 6R+ 2S+ 5T+ 1U+10V+ 4W+ 4X+ 3Y+ 6Z=449
1A+ 5B+ 4C+ 3D+ 8E+ 3F+ 2G+ 3H+ 2I+ 2J+ 5K+ 4L+ 2M+ 5N+ 1O+ 3P+ 2Q+ 3R+ 5S+ 4T+ 4U+ 6V+ 2W+ 2X+ 5Y+ 4Z=449
5B+ 5C+ 4D+ 4E+ 6F+ 4G+ 4H+ 5I+ 1J+ 3K+ 4L+ 2M+ 6N+ 2O+ 4P+ 4Q+ 4R+ 3S+ 3T + 8V+ 1W+ 5X+ 1Y+ 2Z=449
2A+ 3B+ 2C+ 3D+ 8E+ 3F + 1H+ 3I+ 5J+ 7K+ 5L+ 3M+ 5N+ 2O+ 4P+ 2Q+ 3R+ 5S+ 4T+ 5U+ 2V+ 2W+ 3X+ 5Y+ 3Z=449
3A+ 6B+ 5C+ 1D+ 8E+ 2F+ 6G+ 1H+ 4I+ 1J+ 2K+ 2L+ 3M+ 1N+ 4O+ 4P+ 3Q+ 5R+ 8S+ 2T+ 3U+ 7V+ 3W+ 3X+ 1Y+ 2Z=449
2A+ 1B+ 3C+ 2D+ 6E+ 3F+ 3G+ 3H+ 3I+ 5J+ 4K+ 6L+ 4M+ 5N+ 3O+ 3P+ 4Q+ 3R+ 3S+ 3T+ 2U+ 3V+ 4W+ 3X+ 3Y+ 6Z=449
1A+ 1B+ 1C+ 3D+ 6E+ 2F+ 4G+ 4H+ 2I+ 3J+ 3K+ 3L+ 6M+ 2N+ 3O+ 4P+ 6Q+ 5R+ 1S+ 1T+ 6U+ 7V+ 6W+ 2X+ 3Y+ 5Z=449
1A+ 5B+ 1C+ 3D+10E+ 4F+ 1G+ 1H+ 2I+ 3J+ 3K+ 4L+ 5M+ 6N+ 2O+ 4P+ 2Q+ 4R+ 5S+ 1T+ 4U+ 6V + 3X+ 5Y+ 5Z=449
1A+ 3B+ 4C+ 5D+ 7E+ 1F+ 4G+ 4H+ 6I+ 4J+ 3K+ 3L + 2N+ 2O+ 3P+ 5Q+ 1R+ 5S+ 1T+ 7U+ 6V+ 1W+ 4X+ 4Y+ 4Z=449
4A + 2C+ 3D+ 5E+ 3F+ 3G+ 4H+ 2I+ 4J+ 1K+ 3L+ 3M+ 2N+ 5O+ 4P+ 4Q+ 6R+ 4S+ 1T+ 4U+ 7V+ 4W+ 3X+ 5Y+ 4Z=449
1A+ 5B+ 2C+ 2D+ 6E+ 4F+ 5G+ 3H+ 5I+ 1J+ 6K+ 3L+ 4M+ 2N+ 2O+ 3P+ 1Q+ 2R+ 4S+ 4T+ 1U+10V+ 5W+ 3X+ 3Y+ 3Z=449
2A+ 1B+ 2C+ 2D+ 4E+ 4F+ 1G+ 1H+ 6I+ 4J+ 6K+ 4L+ 7M+ 4N+ 7O+ 1P+ 2Q+ 3R+ 4S+ 5T+ 5U+ 2V+ 5W+ 3X+ 2Y+ 3Z=449
3A+ 1B+ 5C+ 1D+ 6E+ 3F+ 3G+ 3H+ 5I+ 4J+ 2K+ 6L+ 3M+ 3N+ 4O+ 2P+ 3Q+ 6R+ 4S + 3U+ 5V+ 5W+ 4X+ 1Y+ 5Z=449
2A+ 4B+ 1C+ 3D+11E+ 2F+ 6G+ 6H+ 7I+ 3J+ 3K+ 2L+ 5M+ 7N + 2P+ 4Q+ 1R + 2T+ 6U+ 4V+ 3W+ 2X+ 2Y+ 2Z=449
2A+ 3B+ 2C+ 6D+ 8E+ 5F+ 2G+ 2H+ 4I+ 2J+ 4K + 2M+ 4N+ 6O+ 2P+ 3Q+ 3R+ 4S + 2U+ 7V+ 7W+ 4X+ 3Y+ 3Z=449
3A+ 7B+ 1C+ 4D+ 8E+ 3F+ 1G+ 2H+ 1I+ 4J+ 1K+ 4L+ 3M+ 5N + 6P+ 1Q+ 3R+ 5S+ 2T+ 2U+ 7V + 6X+ 4Y+ 7Z=449
2B+ 3C+ 4D+ 6E+ 8F+ 3G+ 3H+ 6I + 2K + 2M+ 2N+ 2O+ 5P+ 3Q+ 3R+ 1S+ 4T+ 3U+12V+ 4W+ 5X+ 4Y+ 3Z=449
3A+ 4B+ 4C+ 3D+ 8E+ 1F+ 2G+ 3H+ 1I+ 3J+ 4K+ 3L+ 1M+ 2N+ 5O+ 3P+ 1Q+ 4R+ 6S+ 3T+ 6U+ 5V+ 7W+ 1X+ 3Y+ 4Z=449
4A+ 7B+ 3C + 9E+ 1F + 5I+ 2J+ 2K+ 3L+ 4M+ 2N+ 2O+ 4P+ 4Q+ 4R+ 6S+ 4T+ 6U+ 6V+ 4W+ 3X+ 2Y+ 3Z=449
5A+ 6B+ 1C+ 4D+ 6E+ 2F+ 1G+ 1H+ 5I+ 4J+ 2K+ 2L+ 3M+ 3N+ 6O+ 3P+ 2Q+ 3R+ 6S+ 1T+ 3U+ 8V+ 5W+ 3X+ 4Y+ 1Z=449
5A+ 3B+ 4C+ 1D+ 9E+ 4F+ 5G+ 6H+ 4I+ 1J+ 3K+ 2L+ 2M+ 1N+ 4O+ 1P+ 2Q+ 3R+ 6S+ 2T+ 4U+ 5V+ 1W+ 4X+ 1Y+ 7Z=449
1A+ 2B+ 2C+ 5D+ 4E+ 8F+ 6G+ 3H+ 3I+ 3J+ 2K+ 5L + 8N+ 3O+ 2P+ 1Q+ 3R+ 3S+ 4T+ 5U+ 9V + 3X+ 4Y+ 1Z=449
4A+ 3B+ 5C+ 1D+ 7E+ 5F+ 4G+ 6H+ 4I+ 1J+ 6K+ 5L + 3N+ 4O+ 2P+ 5Q+ 2R+ 3S+ 2T+ 2U+ 5V+ 4W+ 2X+ 4Y+ 1Z=449
2A+ 2B+ 3C+ 2D+ 9E+ 4F+ 5G+ 2H+ 2I+ 5J+ 4K+ 2L+ 2M+ 2N+ 1O+ 5P+ 3Q+ 3R+ 7S + 2U+ 5V+ 4W+ 6X+ 4Y+ 4Z=449
4A+ 1B+ 3C+ 4D+ 7E+ 4F+ 6G+ 2H+ 6I+ 2J+ 4K+ 1L+ 3M+ 5N+ 1O+ 4P+ 2Q+ 1R+ 2S+ 4T+ 4U+ 6V+ 5W+ 3X+ 5Y+ 1Z=449
5A+ 3B+ 2C+ 2D+ 2E+ 5F+ 7G+ 3H+ 1I+ 5J+ 3K+ 7L+ 2M+ 5N+ 4O+ 1P+ 3Q+ 2R+ 2S+ 3T+ 4U+ 6V+ 2W+ 4X+ 3Y+ 4Z=449
7A+ 5B+ 4C+ 2D+ 7E+ 3F+ 5G+ 9H+ 4I+ 3J+ 5K+ 2L+ 2M + 3O+ 2P+ 5Q+ 3R+ 3S+ 2T+ 2U+ 4V+ 1W+ 2X+ 3Y+ 2Z=449
2A+ 5B+ 3C+ 3D+ 6E+ 2F+ 6G+ 6H+ 3I+ 5J+ 5K+ 6L+ 2M+ 4N+ 2O+ 2P+ 4Q+ 2R+ 2S+ 4T+ 2U+ 5V+ 5W + 1Y+ 3Z=449
5A+ 6B+ 3C+ 5D+ 4E+ 3F+ 3G+ 3H+ 2I + 3K+ 4L+ 3M+ 3N+ 1O+ 4P+ 1Q+ 3R+ 4S + 8U+10V+ 4W+ 3X+ 1Y+ 4Z=449
6A+ 6B+ 3C+ 3D+ 6E+ 1F+ 2G+ 3H+ 3I+ 3J+ 5K+ 4L+ 1M+ 4N+ 6O+ 2P+ 5Q+ 2R+ 3S+ 2T+ 6U+ 3V+ 4W+ 3X+ 1Y+ 3Z=449
8A+ 2B+ 5C+ 3D+ 4E+ 5F+ 5G + 3I + 4K+ 5L+ 4M+ 7N+ 3O+ 2P+ 4Q+ 1R+ 5S+ 5T + 3V+ 6W+ 1X+ 2Y+ 3Z=449
4A+ 5B+ 3C+ 4D+ 8E+ 1F+ 2G+ 4H+ 5I+ 1J+ 1K+ 2L+ 6M+ 4N+ 3O+ 3P+ 3Q+ 5R+ 5S + 1U+ 6V+ 3W+ 3X+ 5Y+ 3Z=449
2A+ 4B+ 3C+ 5D+ 7E+ 6F+ 3G+ 3H+ 2I+ 4J+ 2K+ 4L+ 4M + 2O+ 1P+ 6Q+ 2R+ 4S+ 3T+ 3U+ 4V+ 7W+ 2X+ 3Y+ 4Z=449
6A+ 8B+ 4C+ 1D+ 2E+ 4F+ 1G+ 6H+ 2I+ 5J+ 3K+ 3L+ 1M+ 7N+ 2O+ 1P+ 5Q+ 1R+ 2S+ 3T+ 2U+ 7V+ 3W+ 6X+ 1Y+ 4Z=449
3A+ 3B+ 5C+ 4D+ 5E+ 6F+ 1G+ 7H+ 4I+ 3J+ 3K+ 4L+ 2M+ 4N+ 4O+ 4P+ 3Q+ 4R+ 4S+ 1T+ 2U+ 4V+ 2W+ 4X+ 2Y+ 2Z=449
2A+ 1B+ 2C+ 4D+ 6E+ 6F+ 4G+ 4H+ 3I+ 4J+ 3K+ 1L+ 2M+ 4N+ 3O+ 3P+ 4Q+ 4R+ 3S+ 3T+ 5U+ 7V+ 4W+ 3X+ 3Y+ 2Z=449
2A+ 4B+ 4C+ 3D+ 4E+ 1F+ 4G+ 3H+ 6I+ 1J+ 7K+ 4L+ 6M+ 1N+ 3O+ 3P+ 3Q+ 4R+ 2S+ 3T+ 4U+ 7V+ 5W+ 1X+ 4Y+ 1Z=449
2A+ 2B+ 1C+ 3D+ 7E+ 6F+ 4G+ 1H+ 4I+ 3J+ 7K+ 3L+ 1M+ 2N+ 2O+ 4P+ 4Q+ 1R+ 4S+ 1T+ 2U+ 9V+ 4W+ 5X+ 4Y+ 4Z=449
4A+ 5B+ 2C+ 2D+ 3E + 4G+ 6H+ 4I+ 3J+ 7K+ 2L+ 3M+ 6N+ 2O+ 2P+ 4Q+ 1R+ 2S+ 4T+ 5U+ 7V+ 5W+ 3X+ 2Y+ 2Z=449
1A+ 5B+ 4C+ 1D+ 5E+ 1F+ 4G+ 4H+ 5I+ 1J+ 3K+ 5L+ 6M+ 4N+ 5O+ 5P+ 2Q+ 1R+ 3S+ 1T+ 3U+ 8V+ 3W+ 2X+ 4Y+ 4Z=449
6A+ 4B+ 3C+ 4D+ 6E+ 4F+ 5G+ 4H + 1J+ 1K+ 1L+ 3M+ 5N+ 3O + 4Q+ 3R+ 7S+ 5T+ 7U+ 2V+ 2W+ 4X+ 3Y+ 3Z=449
5A+ 3B+ 4C+ 4D+ 5E+ 4F+ 1G+ 3H+ 3I+ 2J+ 6K+ 2L+ 2M+ 5N+ 3O+ 3P+ 6Q+ 2R+ 4S+ 3T+ 3U+ 4V+ 5W+ 3X+ 2Y+ 3Z=449
3A+ 4B+ 4C+ 1D+ 4E+ 2F+ 1G+ 4H+ 1I+ 1J+ 1K+ 5L+ 5M+ 3N+ 3O+ 7P+ 5Q+ 7R+ 8S+ 4T+ 4U+ 4V+ 3W+ 3X+ 2Y+ 1Z=449
2C+ 1D+ 5E+ 2F+ 1G+ 1H+ 2I+ 1J+ 2K+ 3L+ 2M+ 4N+ 1O+ 1P + 3R+ 2S+ 2T+ 1U+ 7V+ 1W + 1Z=191
1A + 3D+ 7E+ 3F+ 1G+ 1H+ 1I+ 2J + 2L+ 1M+ 1N+ 5O + 2Q+ 2R+ 1S+ 4T+ 5U+ 1V + 1X + 1Z=193
1A+ 2B+ 6C+ 2D+ 6E + 2G+ 2H+ 2I+ 1J + 2L+ 2M+ 1N+ 2O + 3Q+ 1R+ 1S + 1U+ 2V+ 3W+ 1X+ 1Y+ 1Z=193
1A+ 2B+ 2C + 2E + 5H + 3J+ 1K+ 1L+ 1M+ 4N + 1P+ 2Q+ 1R+ 3S + 2U+ 9V+ 3W+ 1X+ 1Y =194
2B+ 1C + 5E+ 1F+ 4G+ 3H + 1J+ 2K+ 6L+ 1M + 1O + 3Q+ 1R+ 2S+ 4T+ 1U+ 4V + 2Y+ 1Z=196
1A+ 1B+ 1C+ 3D+ 6E + 1G + 3I+ 1J+ 1K+ 2L+ 2M+ 1N+ 1O+ 2P+ 2Q+ 1R+ 1S+ 1T+ 1U+ 5V+ 2W+ 2X+ 3Y+ 1Z=196
2A + 4D+ 4E+ 2F+ 2G+ 1H+ 1I+ 1J+ 5K+ 4L+ 1M+ 2N+ 1O+ 1P+ 1Q+ 1R+ 2S + 4V+ 2W+ 2X + 2Z=199
2A+ 1B+ 1C+ 4D+ 3E+ 1F+ 2G+ 2H+ 1I + 1K+ 3L+ 2M + 3O + 2Q+ 2R + 2T + 5V+ 1W+ 1X+ 4Y+ 2Z=201
3A+ 1B+ 3C+ 2D+ 5E+ 2F+ 1G+ 1H+ 3I+ 1J+ 2K+ 1L+ 2M + 3O+ 1P+ 1Q+ 1R+ 1S+ 1T+ 2U+ 3V + 2X + 3Z=201
3A+ 3B+ 2C+ 4D+ 3E + 3G+ 4H+ 1I+ 3J + 2M+ 1N+ 3O+ 2P+ 1Q + 2S + 3V+ 2W+ 2X + 1Z=203
3A+ 3B+ 1C+ 3D+ 2E + 3G+ 2H + 1J+ 2K+ 2L+ 3M+ 1N + 2P + 1S+ 2T+ 2U+ 4V+ 1W+ 3X+ 3Y+ 1Z=203
2A + 1C+ 2D+ 4E + 1G+ 1H + 2J + 1L + 2N+ 2O+ 2P+ 2Q+ 4R+ 3S+ 1T + 5V+ 4W+ 3X+ 2Y+ 1Z=204
3B+ 4C+ 2D+ 4E+ 2F+ 4G+ 2H+ 2I+ 3J+ 2K + 1M + 2O+ 1P+ 1Q+ 1R+ 1S+ 1T+ 1U+ 3V + 4X + 1Z=204
2A+ 3B+ 1C + 5E+ 1F+ 2G+ 1H+ 1I + 5K+ 1L + 2N+ 1O + 1Q+ 1R+ 3S+ 3T+ 2U+ 4V+ 3W+ 3X =205
1A+ 1B+ 3C+ 1D+ 2E+ 1F+ 1G+ 3H + 3J+ 4K+ 1L+ 1M + 1O+ 1P+ 1Q+ 1R+ 4S+ 3T + 3V+ 2W+ 3X+ 1Y+ 3Z=206
2A+ 1B+ 1C+ 1D+ 4E+ 1F+ 2G+ 2H+ 3I + 1K+ 1L+ 3M+ 2N+ 2O + 2Q+ 2R+ 2S+ 2T+ 2U+ 5V+ 1W+ 1X+ 1Y+ 1Z=206
2A+ 1B+ 3C+ 2D+ 2E + 3G+ 1H+ 1I+ 1J+ 1K+ 2L+ 2M+ 4N+ 3O+ 1P+ 1Q + 5S+ 2T+ 2U+ 2V+ 2W+ 1X+ 1Y =207
2A+ 1B+ 1C+ 4D+ 2E+ 1F+ 1G+ 2H + 2J+ 1K+ 3L+ 1M+ 5N+ 2O+ 1P+ 5Q+ 1R+ 1S+ 1T+ 2U+ 3V+ 2W + 1Z=207
1C+ 1D+ 2E+ 1F+ 2G+ 4H + 3J+ 1K+ 1L+ 1M + 1O+ 1P+ 3Q+ 2R+ 4S+ 4T+ 1U+ 2V+ 1W+ 5X+ 2Y+ 2Z=208
3A+ 1B + 7E+ 1F+ 1G + 1I + 4K+ 1L + 2N+ 3O+ 3P+ 2Q + 3S+ 2T+ 3U+ 4V+ 2W + 2Z=208
2A+ 2B+ 2C+ 1D+ 3E+ 2F + 2H+ 1I + 1K+ 3L+ 3M + 1O+ 1P+ 3Q+ 2R + 2T+ 3U+ 3V+ 1W+ 3X+ 1Y+ 3Z=208
2A+ 2B+ 1C+ 2D+ 3E+ 2F+ 1G+ 1H+ 2I+ 2J + 2L+ 2M+ 2N+ 4O + 1Q+ 1R+ 2S+ 2T+ 1U+ 4V+ 2W+ 1X+ 3Y =210
3A+ 1B+ 2C+ 1D+ 2E+ 1F+ 2G+ 2H+ 1I+ 1J+ 4K+ 1L+ 2M+ 2N + 2Q+ 2R+ 3S+ 2T+ 2U+ 2V+ 1W+ 4X+ 1Y+ 1Z=210
3A+ 2B+ 3C+ 1D+ 4E+ 4F+ 1G+ 2H + 3J+ 2K + 3M + 1O+ 1P+ 1Q + 2S+ 2T+ 3U+ 2V+ 1W+ 1X + 3Z=210
2A+ 2B+ 3C+ 2D+ 3E+ 2F+ 2G+ 1H + 2L+ 2M+ 2N + 2P+ 2Q + 3S+ 4T+ 1U+ 3V+ 2W+ 1X+ 2Y+ 2Z=211
1B+ 4C+ 3D+ 7E+ 4F+ 2G + 4I+ 1J+ 2K+ 2L+ 3M+ 1N + 3S+ 2T+ 1U+ 1V + 3Y+ 1Z=211
5A+ 1B+ 3C+ 2D+ 8E+ 2F+ 2G+ 2H+ 1I + 1M+ 1N+ 2O+ 2P + 1R+ 2S+ 1T+ 4U + 1W+ 1X + 3Z=211
1B+ 1C+ 1D+ 4E + 2G+ 2H+ 2I + 1K+ 4L+ 1M+ 1N+ 4O+ 2P+ 1Q + 2S+ 3T+ 3U+ 3V+ 1W+ 1X+ 4Y+ 1Z=212
1A + 2C+ 2D+ 3E+ 1F+ 3G+ 3H+ 2I + 3K + 5N+ 2O+ 2P+ 1Q+ 2R+ 1S+ 1T+ 2U+ 3V+ 2W+ 4X =213
1A+ 2B+ 3C+ 2D+ 4E+ 1F+ 2G+ 1H+ 1I+ 1J + 2L+ 2M+ 1N + 3P+ 3Q+ 2R+ 1S+ 3T+ 2U+ 2V+ 4W+ 1X+ 1Y =213
2A+ 1B+ 1C+ 3D+ 2E+ 1F+ 2G+ 1H+ 1I+ 1J+ 1K+ 3L+ 2M+ 2N+ 2O+ 1P+ 1Q+ 1R+ 3S + 2U+ 3V+ 3W+ 3X+ 1Y+ 2Z=214
1B+ 4C+ 2D+ 3E+ 2F+ 2G + 4I+ 3J+ 1K+ 3L+ 3M + 1O+ 2P + 1R+ 1S+ 2T+ 1U+ 1V+ 2W+ 3X+ 1Y+ 2Z=215
1A+ 2B+ 3C + 3E+ 3F + 2H+ 2I+ 1J+ 1K+ 2L+ 1M+ 2N+ 4O+ 2P+ 2Q+ 2R+ 1S + 1U+ 4V + 3X+ 2Y+ 1Z=215
2A+ 1B+ 1C + 2E+ 2F + 2H+ 2I+ 3J+ 1K+ 1L+ 1M+ 3N+ 2O+ 4P+ 1Q+ 2R + 1T+ 3U+ 6V+ 2W+ 2X + 1Z=216
2A+ 2B + 1D+ 3E + 2G+ 2H+ 1I+ 2J+ 2K+ 4L+ 3M+ 3N+ 3O+ 4P+ 5Q + 1S + 1U + 1W+ 2X + 1Z=216
4A+ 2B+ 3C+ 2D+ 2E + 2H+ 2I + 1K+ 1L+ 1M + 3O + 2Q+ 2R+ 2S + 4U+ 4V+ 6W+ 1X+ 1Y =216
1A+ 2B+ 4C + 4E+ 6F + 2J + 2L + 2N+ 1O+ 3P+ 1Q + 1S + 3U+ 7V+ 2W + 3Y+ 1Z=216
2A+ 3B+ 1C+ 5D+ 4E+ 3F+ 1G+ 1H+ 1I+ 2J+ 1K+ 4L+ 2M+ 3N + 1P + 2R+ 1S + 2U+ 2V+ 1W+ 1X+ 1Y+ 1Z=217
2A+ 1B+ 2C+ 1D+ 5E+ 2F + 1H + 2J+ 4K+ 1L+ 2M+ 1N+ 1O + 1Q+ 3R+ 2S+ 1T+ 2U+ 1V+ 4W+ 2X+ 2Y+ 2Z=218
2A+ 3B+ 2C + 3E+ 1F+ 5G+ 1H+ 1I+ 2J+ 1K+ 1L+ 2M+ 2N + 2P+ 2Q+ 1R+ 1S+ 2T+ 2U+ 4V+ 1W+ 2X+ 2Y =218
1A+ 2B+ 3C+ 2D+ 3E+ 4F + 3K+ 4L + 1N+ 2O+ 1P + 1R+ 4S+ 1T+ 3U+ 4V+ 4W + 1Y+ 1Z=219
2A + 4C + 2E+ 1F+ 1G+ 2H+ 4I+ 2J+ 2K + 3M+ 1N+ 2O+ 2P + 3R+ 5S + 5V + 1X + 3Z=219
2C+ 2D+ 3E + 4H+ 1I+ 1J+ 2K + 1M+ 2N+ 3O+ 2P+ 2Q+ 3R+ 3S + 1U+ 2V+ 2W+ 4X+ 4Y+ 1Z=219
1B+ 2C+ 1D+ 4E+ 2F+ 1G + 3I+ 1J+ 4K+ 2L+ 2M+ 1N+ 1O+ 2P+ 2Q+ 3R+ 1S+ 1T+ 2U+ 2V+ 2W+ 3X+ 2Y =221
1B+ 4C+ 3D+ 5E+ 3F + 3H+ 1I+ 1J+ 1K + 1M+ 2N+ 1O+ 4P+ 1Q+ 1R+ 1S+ 1T+ 3U + 3W+ 2X+ 1Y+ 2Z=225
3A+ 1B + 1D+ 3E+ 2F+ 3G + 3I+ 1J+ 5K+ 3L+ 2M+ 2N+ 2O + 1R + 3U+ 3V+ 2W+ 2X+ 1Y+ 2Z=226
3B+ 2C + 4E+ 2F+ 1G+ 2H+ 1I+ 4J+ 2K+ 1L+ 1M+ 1N+ 1O+ 3P+ 2Q+ 2R+ 1S+ 2T+ 1U+ 3V+ 2W+ 1X+ 1Y+ 2Z=228
2A + 2D+ 2E+ 3F+ 3G+ 3H+ 5I+ 1J+ 1K+ 3L+ 3M+ 3N+ 2O+ 1P+ 1Q + 1S + 4V+ 1W+ 1X+ 1Y+ 2Z=228
2D+ 3E+ 1F+ 2G+ 4H+ 4I+ 1J+ 3K+ 2L+ 1M+ 2N+ 1O + 3R+ 1S+ 2T+ 2U+ 1V+ 2W+ 5X+ 2Y+ 1Z=228
4A+ 1B + 3E + 3G + 3I + 3K+ 2L+ 3M+ 2N+ 2O+ 3P+ 2Q+ 3R+ 1S + 1U+ 5V+ 1W + 3Z=229
2A+ 4B+ 2C + 3E+ 1F+ 3G + 1J + 2L+ 1M+ 4N+ 1O + 3Q+ 1R+ 3S+ 2T+ 1U+ 3V+ 1W+ 2X+ 3Y+ 2Z=229
2A+ 3B+ 2C+ 1D+ 4E+ 4F+ 2G+ 3H+ 2I + 2K+ 1L + 1N+ 2O+ 1P+ 1Q+ 1R+ 2S+ 1T+ 2U+ 4V+ 1W+ 1X+ 1Y+ 1Z=229
1A + 3D+ 2E+ 2F+ 1G+ 1H+ 1I + 3K+ 1L+ 2M+ 1N + 2P+ 4Q+ 3R+ 1S+ 1T+ 2U+ 3V+ 4W+ 3X+ 3Y+ 1Z=229
1C + 3E+ 1F+ 2G+ 4H+ 4I+ 1J+ 1K+ 1L+ 1M+ 3N+ 1O+ 2P+ 2Q + 3S + 3U+ 5V + 2X+ 3Y+ 2Z=230
1A+ 2B + 1D+ 3E+ 1F+ 1G+ 4H+ 1I+ 1J+ 1K+ 2L+ 1M+ 2N + 2P+ 1Q+ 4R+ 2S+ 3T + 4V+ 1W+ 2X+ 2Y+ 3Z=231
1A+ 2B + 3D+ 3E+ 3F+ 1G+ 1H+ 2I+ 1J+ 1K+ 1L+ 4M + 1O+ 2P+ 1Q+ 2R+ 3S + 5V+ 4W + 3Y+ 1Z=231
2A+ 2B+ 1C+ 1D+ 3E + 4G+ 3H+ 2I + 3K+ 1L + 2N+ 1O + 2Q + 4S+ 1T+ 2U+ 4V+ 2W+ 1X+ 2Y+ 2Z=232
2A+ 3B+ 1C+ 2D+ 2E+ 2F+ 1G+ 2H+ 2I+ 3J+ 2K+ 1L+ 1M + 1O+ 1P+ 1Q+ 2R+ 4S+ 1T+ 2U+ 3V+ 2W+ 2X+ 1Y+ 1Z=232
1A+ 2B + 2D+ 4E+ 1F+ 2G+ 5H+ 1I+ 2J + 1L+ 2M+ 3N+ 2O + 3Q+ 1R+ 4S + 1V+ 3W+ 1X+ 3Y+ 1Z=233
3A+ 2B + 1D+ 1E+ 2F+ 2G + 4K + 4M+ 1N+ 3O+ 1P+ 1Q+ 1R+ 2S+ 2T+ 3U+ 3V+ 4W+ 1X+ 2Y+ 2Z=233
1A+ 4B+ 1C+ 1D+ 5E+ 1F+ 5G+ 1H+ 2I+ 2J + 3L+ 1M+ 2N+ 2O+ 2P + 2S + 1U+ 2V+ 6W+ 1X =233
2A+ 3B+ 2C + 1F+ 2G+ 1H+ 3I+ 3J+ 1K+ 6L + 2N + 2P + 2R + 2T+ 3U+ 4V+ 2W+ 2X+ 1Y+ 1Z=233
2A+ 5B+ 1C+ 2D+ 4E + 1I+ 1J+ 3K + 1M+ 2N + 1P+ 4Q+ 1R+ 2S+ 1T+ 2U+ 5V+ 1W + 2Y+ 4Z=233
1B+ 3C+ 1D+ 2E+ 1F + 1H+ 4I+ 3J+ 3K+ 1L + 1N+ 3O+ 1P+ 2Q+ 2R+ 3S + 3U+ 3V + 2X+ 4Y+ 1Z=234
3B+ 1C+ 2D+ 3E+ 4F+ 1G+ 2H+ 3I+ 1J+ 2K+ 2L + 3O+ 4P+ 2Q + 1S+ 2T+ 2U+ 4V+ 1W + 1Y+ 1Z=236
4A+ 1B+ 2C + 2E + 1H+ 4I+ 3J+ 2K+ 1L+ 1M+ 2N+ 1O+ 3P+ 2Q+ 3R+ 3S + 3V+ 2W+ 2X + 3Z=236
1A+ 1B + 1D+ 5E+ 4F+ 1G + 1I+ 2J+ 3K+ 1L+ 2M+ 2N+ 2O+ 4P + 2R+ 4S+ 3T + 3W+ 1X+ 1Y+ 1Z=236
2B+ 3C + 3E + 3G+ 2H+ 1I + 3K + 2M+ 1N+ 2O+ 2P+ 1Q+ 3R+ 3S+ 1T+ 1U+ 4V+ 1W+ 1X+ 1Y+ 5Z=236
1A + 1C+ 2D+ 3E+ 2F+ 1G+ 1H+ 2I + 2K+ 4L+ 1M+ 3N + 4P+ 2Q+ 2R+ 3S+ 1T+ 4U+ 1V+ 2W+ 1X+ 1Y+ 1Z=236
3A+ 2B + 2D+ 2E+ 4F+ 3G + 1I + 2K + 1M+ 1N+ 3O+ 1P+ 2Q+ 2R+ 3S+ 1T+ 1U+ 3V+ 2W+ 3X+ 2Y+ 1Z=238
2A + 2D+ 1E+ 2F+ 3G+ 2H+ 5I+ 3J+ 3K+ 2L + 2N + 1P + 2R+ 2S+ 4T+ 3U+ 3V + 1X+ 1Y+ 1Z=239
1A+ 2B+ 1C + 5E+ 4F+ 3G+ 1H+ 2I+ 1J + 1L+ 3M+ 1N+ 1O+ 1P+ 1Q+ 5R+ 2S+ 1T+ 3U+ 3V+ 1W + 2Y =239
2A + 2D+ 3E+ 3F+ 1G+ 1H+ 3I+ 3J+ 2K+ 1L+ 1M+ 5N+ 1O+ 1P+ 1Q+ 2R+ 1S+ 3T + 2V+ 2W + 4Y+ 1Z=241
1A+ 4B + 1D+ 5E+ 3F + 2I+ 3J+ 2K+ 2L+ 2M+ 3N+ 1O+ 2P+ 2Q+ 1R + 3T+ 2U + 1W+ 1X+ 1Y+ 3Z=241
1A+ 3B+ 4C+ 3D+ 4E+ 5F+ 2G+ 3H+ 1I + 1K+ 2L+ 1M+ 1N + 2P+ 1Q+ 1R+ 2S+ 1T + 1V+ 2W + 4Z=242
2A+ 2B + 3D + 1F+ 4G+ 2H+ 3I+ 1J+ 2K+ 2L+ 2M+ 2N + 1P+ 4Q+ 1R+ 1S+ 3T+ 3U+ 1V + 2X + 3Z=244
5B + 2D+ 2E + 2G+ 2H+ 3I+ 1J+ 2K+ 1L+ 3M+ 2N+ 2O+ 2P+ 1Q+ 2R+ 2S + 2U+ 2V+ 2W+ 3X+ 1Y+ 1Z=245
1A+ 2B+ 1C + 2E+ 1F+ 2G+ 1H+ 2I+ 4J + 1M+ 3N+ 2O + 1Q+ 4R + 4T+ 1U+ 3V+ 5W+ 1X + 4Z=246
5B + 1D + 1F+ 3G + 1J+ 1K+ 2L+ 1M+ 2N + 7Q+ 2R+ 2S+ 2T+ 3U+ 5V+ 3W+ 1X+ 1Y+ 2Z=247
4B+ 1C+ 1D+ 3E+ 2F+ 1G + 1I+ 1J+ 2K+ 1L + 4N+ 1O+ 1P+ 2Q+ 2R+ 4S+ 1T+ 1U+ 4V+ 2W+ 1X+ 4Y+ 1Z=248
1A + 3C + 3E+ 2F+ 2G+ 1H+ 2I + 2K+ 2L+ 1M+ 4N+ 1O+ 3P+ 1Q+ 1R+ 2S+ 1T+ 2U + 2W+ 2X+ 5Y+ 2Z=249
3B+ 1C+ 1D+ 1E+ 1F+ 2G+ 4H+ 2I+ 1J+ 2K+ 1L+ 2M+ 1N+ 4O+ 1P+ 1Q+ 4R+ 3S + 3U+ 2V+ 2W+ 1X+ 1Y+ 1Z=251
4B + 2D+ 5E+ 3F + 1H+ 3I+ 1J+ 3K + 2M+ 1N+ 2O+ 2P + 2R + 4U+ 3V+ 3W + 2Y+ 2Z=252
2A+ 3B+ 1C + 1E+ 2F + 1H+ 2I+ 4J + 2L+ 2M+ 2N + 3P+ 4Q+ 1R+ 4S+ 1T+ 2U+ 1V+ 2W+ 1X+ 1Y+ 3Z=255
1A+ 7B + 2D+ 4E + 2G+ 1H + 2K+ 2L + 4N+ 3O+ 2P+ 3Q+ 1R+ 2S + 2U+ 1V+ 1W+ 1X + 4Z=255
4A+ 3B + 1D+ 1E+ 3F+ 1G+ 4H+ 3I + 2K+ 2L + 3N+ 1O+ 2P+ 1Q+ 3R+ 1S+ 1T+ 2U+ 3V + 1X+ 1Y+ 2Z=258
1A+ 1B + 1D+ 5E+ 4F+ 1G+ 2H+ 4I+ 1J+ 2K+ 1L + 1N + 2P+ 2Q+ 1R+ 2S+ 2T+ 2U+ 1V+ 1W+ 1X+ 4Y+ 3Z=260
4A+ 6B+ 2C+ 3D+ 1E+ 3F+ 2G+ 2H+ 3I + 1L+ 1M+ 1N + 2P+ 2Q+ 1R+ 1S + 1U+ 2V+ 1W+ 2X+ 2Y+ 2Z=261
2A+ 5B+ 1C+ 1D+ 1E+ 1F+ 3G+ 2H+ 2I+ 1J+ 3K + 2M+ 2N + 4Q+ 1R+ 2S + 1U+ 3V+ 3W + 2Y+ 3Z=264
3A+ 2B + 1F+ 1G+ 1H+ 4I+ 2J+ 2K+ 1L+ 2M+ 2N+ 1O+ 3P+ 2Q+ 2R+ 4S+ 1T+ 1U+ 1V+ 1W+ 2X+ 2Y+ 4Z=271
The Corresponding Solution

|
You may be content with trying to solve these puzzles using brute force.
Go right ahead.
I dare you.
I, too, enjoy the challenge to my intuition associated with trial and error.
But only up to a point.
When my intuition fails me, as it often does, I employ my last resort.
I fall back upon the school-boyish, elimination method.
There is no shame in solving these puzzles analytically.
Which is easy for me to say, but hard for you to do.
So, I made the situation fair for everyone.
I published a companion piece.
It contains all 146,853 pairs of the checksums required to set up the 146,853 systems of linear equations:
(a) The common linear checksum (e.g. 449 ).
(b) The first of the ninety columnar checksums (e.g. 191).
Each benign cheat is four-parted (e.g. 1, 1, 449, and 191):
(a) The volume number within the book series.
(b) The relative puzzle number within the volume.
(c) The common linear checksum of the pertinent puzzle.
(d) The first columnar checksum of said puzzle.
The First Page Of The All-In-One Cheat Sheet
1 1 449 191 1 51 427 178 1 101 452 191 2 4 453 184 2 54 442 176 1 2 432 173 1 52 471 194 1 102 454 183 2 5 448 188 2 55 457 190 1 3 448 179 1 53 473 195 1 103 470 190 2 6 437 175 2 56 459 195 1 4 452 193 1 54 471 190 1 104 458 192 2 7 472 201 2 57 470 186 1 5 463 183 1 55 459 192 1 105 450 183 2 8 462 190 2 58 429 169 1 6 442 178 1 56 473 201 1 106 467 188 2 9 438 172 2 59 466 187 1 7 433 173 1 57 431 172 1 107 464 197 2 10 441 182 2 60 457 192 1 8 466 192 1 58 437 176 1 108 425 180 2 11 437 180 2 61 474 191 1 9 440 171 1 59 440 193 1 109 474 189 2 12 474 196 2 62 445 183 1 10 472 202 1 60 459 196 1 110 466 198 2 13 434 172 2 63 459 196 1 11 428 157 1 61 461 194 1 111 473 185 2 14 469 197 2 64 437 174 1 12 453 183 1 62 474 197 1 112 474 205 2 15 445 174 2 65 463 193 1 13 437 174 1 63 427 171 1 113 466 199 2 16 459 192 2 66 425 172 1 14 441 187 1 64 471 190 1 114 426 174 2 17 451 183 2 67 439 174 1 15 435 179 1 65 443 187 1 115 474 202 2 18 453 181 2 68 438 180 1 16 455 189 1 66 430 168 1 116 454 185 2 19 439 183 2 69 468 198 1 17 453 180 1 67 470 195 1 117 441 181 2 20 432 173 2 70 436 182 1 18 451 179 1 68 462 195 1 118 465 184 2 21 433 176 2 71 472 198 1 19 450 193 1 69 466 188 1 119 443 179 2 22 438 184 2 72 458 189 1 20 438 178 1 70 450 181 1 120 441 183 2 23 473 203 2 73 431 182 1 21 456 179 1 71 431 178 1 121 451 183 2 24 469 198 2 74 431 180 1 22 425 159 1 72 459 185 1 122 444 185 2 25 447 182 2 75 433 179 1 23 462 190 1 73 460 193 1 123 442 182 2 26 464 194 2 76 467 182 1 24 457 185 1 74 457 188 1 124 427 170 2 27 439 178 2 77 440 187 1 25 443 182 1 75 437 178 1 125 436 184 2 28 466 195 2 78 457 189 1 26 428 170 1 76 448 169 1 126 463 203 2 29 437 184 2 79 468 195 1 27 452 184 1 77 440 177 1 127 470 189 2 30 461 191 2 80 472 197 1 28 439 177 1 78 452 183 1 128 459 180 2 31 429 174 2 81 426 169 1 29 449 186 1 79 469 197 1 129 455 183 2 32 445 184 2 82 469 193 1 30 470 196 1 80 468 191 1 130 453 187 2 33 452 184 2 83 473 196 1 31 465 200 1 81 461 199 1 131 428 167 2 34 457 186 2 84 426 165 1 32 467 191 1 82 466 196 1 132 425 168 2 35 474 203 2 85 425 173 1 33 457 188 1 83 468 194 1 133 445 180 2 36 432 178 2 86 425 173 1 34 444 176 1 84 449 188 1 134 450 182 2 37 433 179 2 87 440 174 1 35 470 200 1 85 451 183 1 135 431 171 2 38 446 181 2 88 450 188 1 36 457 187 1 86 432 173 1 136 427 170 2 39 433 173 2 89 453 184 1 37 427 166 1 87 452 185 1 137 461 206 2 40 454 187 2 90 429 177 1 38 446 176 1 88 452 186 1 138 473 197 2 41 446 180 2 91 471 195 1 39 448 190 1 89 456 181 1 139 429 180 2 42 473 199 2 92 438 178 1 40 465 199 1 90 464 178 1 140 464 188 2 43 434 168 2 93 449 188 1 41 454 186 1 91 440 178 1 141 432 177 2 44 465 187 2 94 457 177 1 42 461 186 1 92 426 169 1 142 447 180 2 45 447 180 2 95 443 178 1 43 438 170 1 93 462 187 1 143 429 181 2 46 428 173 2 96 431 179 1 44 442 171 1 94 465 184 1 144 461 185 2 47 473 199 2 97 428 183 1 45 473 199 1 95 428 166 1 145 471 193 2 48 428 177 2 98 465 187 1 46 468 199 1 96 474 200 1 146 445 181 2 49 474 197 2 99 459 196 1 47 431 172 1 97 472 192 1 147 469 196 2 50 452 182 2 100 444 190 1 48 451 182 1 98 472 196 2 1 470 196 2 51 474 199 2 101 440 187 1 49 448 185 1 99 441 178 2 2 437 180 2 52 472 200 2 102 456 183 1 50 460 190 1 100 471 192 2 3 463 191 2 53 438 188 2 103 435 180
4,699,296 Bookend Puzzles by Francis Gurtowski
|
This is yet another serious, serious series of 999 books created by Francis Gurtowski.
The prolific author is an authentic, ancient coder, going all the way back to IBM Poughkeepsie (Building 705, no less, second floor) and the heyday of OS/360, Robert Rex Seeber Jr. and the horizontal-microcoded System/360 Model 50, coding pads and the coding-pad veto, punch cards and keypunch machines, and self-modifying code. Francis Gurtowski is also a self-styled Henry Ford of contemporary, do-it-yourself, print-on-demand, book publishing. Henry Ford is synonymous with the assembly line, a perfected process for swiftly turning out a series of ingenious, finished products in a foolproof, mechanically-efficient manner. Once again, each of these sequels takes full advantage of (Amazon) Kindle Direct Publishing's twin, generous, upper limits of 590 bound-and-paperbacked, 8.5x11-inch pages. Each volume contains 4,704 Bookend Puzzles. The concept is simple enough. Each Bookend Puzzle consists of a 132-place row of decimal digits formed by concatenating some 24-36 prime numbers ranging from 101 to 999983. The challenge is to separate the given row into its components i.e. find and mark all of the pertinent prime numbers hidden in plain sight. |
A prime number is a school-boyish counting number with exactly two factors, namely 1 and the number itself.
Here is such an aforesaid row:
21152259574687254899263358157527959348745751 Now here I have broken the row down into its intended constituents:
21152259574687254899263358157527959348745751 The concatenated components of the row, in a row, are 211, 52259, 574687, 254899, 263, 358157, 5279, 593, 487457, 516829, 281243, 991, 6827, 17419, 1259, 592139, 2767, 9613, 484751, 4973, 52457, 363329, 37781, 89521, 254993, 7727, 431, and 5521. If you accept the premise that a prime number is analogous to a word, then a Bookend Puzzle is a counterpart of a word search puzzle with certain cosmetic deviations, namely (a) a row does not rigorously fit the accepted notion of a grid, (b) a list of the prime numbers that are sought after is not provided to you, and (c) Bookend Puzzles are not topical; the common theme of one and all is prime numbers per se. |
Here is a hint.
You might want to try solving Bookend Puzzles by recursively pruning the respective rows outside-in, i.e. alternatively left-to-right and right-to-left and lopping off the bookends. With respect to the row shown above, 211 is definitely the first component because the alternative, i.e. 2115, is excessively factorable: 3, 5, 9, 15, 45, 47, 141, 235, 423, and 705. Okay, so far. Here is a rub: on the opposite end of the row, both 521 and 5521 are candidates inasmuch as both are indeed prime numbers. But, look, not 15521; the third option is excessively factorable: 11, 17, 83, 187, 913, and 1411. Bet on 5521 to be the rightmost component inasmuch as every multiple-place, decimal number ending in 5 is excessively factorable by definition. And so on. |
211522595746872548992633581575279593487457516829281243991682717419125959213927679613484751497352457363329377818952125499377274315521 ...52259574687254899263358157527959348745751682928124399168271741912595921392767961348475149735245736332937781895212549937727431.... .........74687254899263358157527959348745751682928124399168271741912595921392767961348475149735245736332937781895212549937727....... ..............25489926335815752795934874575168292812439916827174191259592139276796134847514973524573633293778189521254993........... ....................26335815752795934874575168292812439916827174191259592139276796134847514973524573633293778189521................. .......................358157527959348745751682928124399168271741912595921392767961348475149735245736332937781...................... .............................5279593487457516829281243991682717419125959213927679613484751497352457363329........................... .................................593487457516829281243991682717419125959213927679613484751497352457................................. ....................................4874575168292812439916827174191259592139276796134847514973...................................... ..........................................516829281243991682717419125959213927679613484751.......................................... ................................................281243991682717419125959213927679613................................................ ......................................................99168271741912595921392767.................................................... .........................................................6827174191259.............................................................. .............................................................174191259.............................................................. .................................................................91259..............................................................

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
146,853 Homophonic Prepper-Primes-Puzzles by Francis Gurtowski
|
This is yet another serious, serious series of 999 books created by Francis Gurtowski.
The prolific author is an authentic, ancient coder, going all the way back to IBM Poughkeepsie (Building 705, no less, second floor) and the heyday of OS/360, Robert Rex Seeber Jr. and the horizontal-microcoded System/360 Model 50, coding pads and the coding-pad veto, punch cards and keypunch machines, and self-modifying code.
Francis Gurtowski is also a self-styled Henry Ford of contemporary, do-it-yourself, print-on-demand, book publishing. Henry Ford is synonymous with the assembly line, a perfected process for swiftly turning out a series of ingenious, finished products in a foolproof, mechanically-efficient manner. Once again, each of these sequels takes full advantage of (Amazon) Kindle Direct Publishing's twin, generous, upper limits of 590 bound-and-paperbacked, 8.5x11-inch pages. The concept is simple enough. Each puzzle consists of a sparse 45x45 block of alphabetic text which you have to translate into a sparse 45x45 block of decimal text. Replace each letter A-Z with a digit 1-9. |
A prime number is a school-boyish counting number with exactly two factors, namely 1 and the number itself.
If you accept the premise that a prime number is analogous to a word, then a Homophonic Prepper-Primes-Puzzle is a counterpart of a crossword puzzle with certain cosmetic deviations, namely (a) the free-range layout of the resulting niches of the puzzle was not predetermined by an articulated grid, (b) the clues, such as they are, which is not much, are statistical rather than literary, and (c) the puzzles are not topical whatsoever; the common theme of one and all is prime numbers per se. Be advised that in order to make your decryption experience even more challenging - and thus much, much, much more rewarding - than it would ordinarily be, there is a catch in my approach to my separate encryptions of the 45x45-square, open-plan crosswords. Not content to simply substitute precisely one ciphertext letter per plaintext letter (decimal digit), I instead more or less arbitrarily substitute one or more ciphertext letters for each plaintext letter (decimal digit). |
So I do not use a simple substitution cipher.
I instead resort to what is called homophonic coding. According to Merriam-Webster, a homophone is one of two or more words pronounced alike but different in meaning or derivation or spelling - such as the words to, too, and two. Conventual homophonic coding not only camouflages but also distorts the patented statistics of the English language, which are common knowledge amongst Scrabble aficionados. The decimal-digit statistics of the prime numbers are yet to be patented. With a simple substitution cipher, if the respective frequencies of the plaintext crossword approximate normality then the same will be said of the ciphertext crossword - only spread differently. A simple substitution cipher is comparatively a piece of cake to attack with paper and pencil. Homophonic encoding, on the other hand, is absolutely a beast. |
A Specimen of the Ciphertext
Across
LWYDJH TZDTFS M LRCTHC O MQBO UTVTBH VAMX
VGOTZO Q IRCJJB M OIDWAW V K Q M U Q
KJDWBG DUSNQO F TTZLZJ W OWCJIO M AMKZKP
MME AEJPZ OZFFRT YGCTKB I D FFTGOX K UXN
YWCZFP CBJJYP A DIOBP F KJJWIX W I B M Q Q
L G N WRG SDGWMO KFFWYG F JWEAXC W STYRE
P G L S O N A D F Z NPUUP U H
HAGSIX YQMLOS QLPMHS MTBJAN CFWGXG F U QPVG
O R C YDPMO C VAH T CIN F V K B LGCNHS B
H Z U M V KVUF U T UCN E PMJVG O H U NATZ
AAEED J GQYE XWDOWN JJFAUG I V LBWAJG G E O
J V GVLSVH QUPPO A W E GLCEBW A ZTWKAX I
IKPJVZ D L LFZWTC APSRYX N WWROKW N M
S R APVLVX U D T N J VUCWAN Z N T UBG GWX
VDBVBX W YOYMVC F A M B Y T CMJZVH U T K C
P C TFFZPE W R NFCRGH L P WYKXP ZTPAG
U A V F VWWLES JGS NYNQAC P V IBTWID Z Z
SVCLHN P N I M P E O ZWFOKX N A MMN
V T JDJVRN QUULMC NGEQMN D Z DBEKYO PCJVX
DSBVZ T F PTBQR W XUJ D B Z G A E S L U
O WXEFLD R D VYE M WBPZVP GCFBXH O OJFDMH
AVX G V G YCEEX ONH M H D DGLHYO G CPP
G KXIWH L ZQND IMKSCE OHNIAP UYO DTJKSO
XFVD S M QLHOVN NKBCAN F G R JZLEFO E AUP K
Q BTHDLW Y GOOWHT T VZBEIE I L H H Y LDFAB
N D B G XNVG W DJFSCO O D XJDJMX VWCTNX Z C
ZSXAQX N Q O V Z AKGZZS EVEHCO B C H A
DSN JCWCVN NYUFJ ANGDDH H JTBSTP Q ATJWMX G
NBS W F MEC D X W W Y FHREKO V TVFH
GRUX UEFRYN O HZJS OYWCYZ YBEYO YSZS VZATTN
YDJJO W G JHBP A YQN A H A W EEXFEP X G U
HZSZ HKBRAG TARCHS LJEVQX I P Y L X
G E G N PLCO S OZNVS W D SIETF UCDVUH N
A H Q I P H N B B AYRZTX G G X H RKETAW
UAOFXE AVNAF MEBT V W X N A UJFANS A
VIW Z N K Q S W BCFDN VDZJQO GIMW PHFCVH
EWFVBB UEUETN Y P Y RJVCEF W C Q YRTBUN A
P CHZPAN A NJRCXH E T X C HRJDNX YHH XWVN
SWAHKH WJTVIO T H NHWFDH SDRVW T TDSAPH T W
NOOUOP X VMJS C M X S DBQCHH UFCASG W
D R YMIROZ OKP MLYSR WWZKGP E OMGOAJ BMDMNZ
XBWNJG W BHABRG E F Z J P Y T Y EFNGCS P
A W R V M P B TLZDKZ M MWFCQX L RQTOW
RPJTVG HCDJHX VMRVH E LGEWVD N Y V XRWAPP
G C S O P RCPTGC P YPEGAN ZDAS
|
Down
L K Y OHAJIS D AGXQNZ NGYHG UVEPSN X R W JMWLPH A K VPUSVS V F SDBRDZ AAIW WODBAP YVDMC ARZEVP D V BOX V XSSUJS OWFCAO W J DGWEZG G E JRBCAC V KDBDAN XJZEHF VHHURN T JOB F GSCUD V V LTZWGX T Q O XZBZKO JWVG HTGAPN I ZABTVH X ISHBXJ U H E BPHPYG G Z E LXYMJG PXF NJTEVW D CWEWKG A M TODJCW D V V F D F HMLGNW F B QANUNW IWRHC Z UPBRS P LDLWZF JFLG W CFRGRN V E J R C DQSZJG YMVGS V P V D Q X V Y A INKUAT OBVDS T N J OQO QVLXYE PRP Y LYN NMNJGP A E VXZH J F Q Y M KYH O V NTRCLH V E H LPFQT I AMHO SIOOPS LCVE LUYWWN B E O GQNCOB C NNOVOB X R Z DNO U F M W QDEZVG Y P OHMS J MKRP MCFFAG SVFXQZ VRLIQR XQNOW U H T E YRTJPG V J F W A WUWDC E U V N O FDZAAS B C S M J R M QHUDPT S U Y DNWDOJ J R NTWPXH MEBRP LBTTDO L OPCTFN MLWEO KHJ SYCO H L V R T I APTTWO F M N BTFVAX QHZBVB N YFTHR CMZ O M N ANACJ CXMHIC S N ONSN CYEHCS L C T LYBKDH U P RGP U MATCZG Y VBWF W RZZEP HOZGPF SCCJAS MGS NJWMKN O DWWALS D F D T CIJC F INJ R H G B S V D C J A NRTDMW KLG D TFWFMN FWYJB NEEDP CFZOAH YHEWYX J H WJZGC W K Y T A X Y Q Z E B K Z V R V Z E OAWBKG BFEUE V N MBVH E G Q Z CXSXKP W W J J G UYLQON P OGIDZH YAXDTN E D G MVP M OIJF AVP G C A H E Z B X VFCRSP D QVW W N MILNWT CZDZG N XSJWEW S D V B C I J C A W CDIRIJ T Y IIGAZW WDEYMN OKJDXJ CKVVE N F F A DEBYOE E J H B W Y I W F G B C POZGB PJLJVS EPTG QCRTQO FYP UQOFWE W LWWZMP K X Z METFYX F O J CMTC E T F AZGBOB W J VXDAHD L XHPHSF QDTHG QVG V T X X WARNZW B GUEH C RZEYUX G NDHOYX A TMMGIC G A O VYINEE LYF VOQESP C UIYXS A N B O N LHJ KTHKB K OHOOHW K LDHJMR AUJELX H XBWPFG GZW XTAYS Y CBAOVX V FWTYPF F R A U C T UUPW O OODEYT T Z U A BHHCBN W M UUNUGW B I J T NCJVAG HRNPUH AMG A UKKMSP H K GTZDMP FGJALX W T KSHN TSDCRP V Z T QSNEAN T MCLD KUD HMTTUX E F X GMSQPZ A KUQYUP A X GKPZNJ MCSPFZ XVN NTACAW N T D MQPX R VBTO W A VUHPO A F A V VWWZPO A X NQEHG Z IMXCGZ X P KBCAGH W H N W S |
The Corresponding Relative Frequencies
Of The Letters Of The Alphabet In A Census
Of The Said Specimen Of The Ciphertext
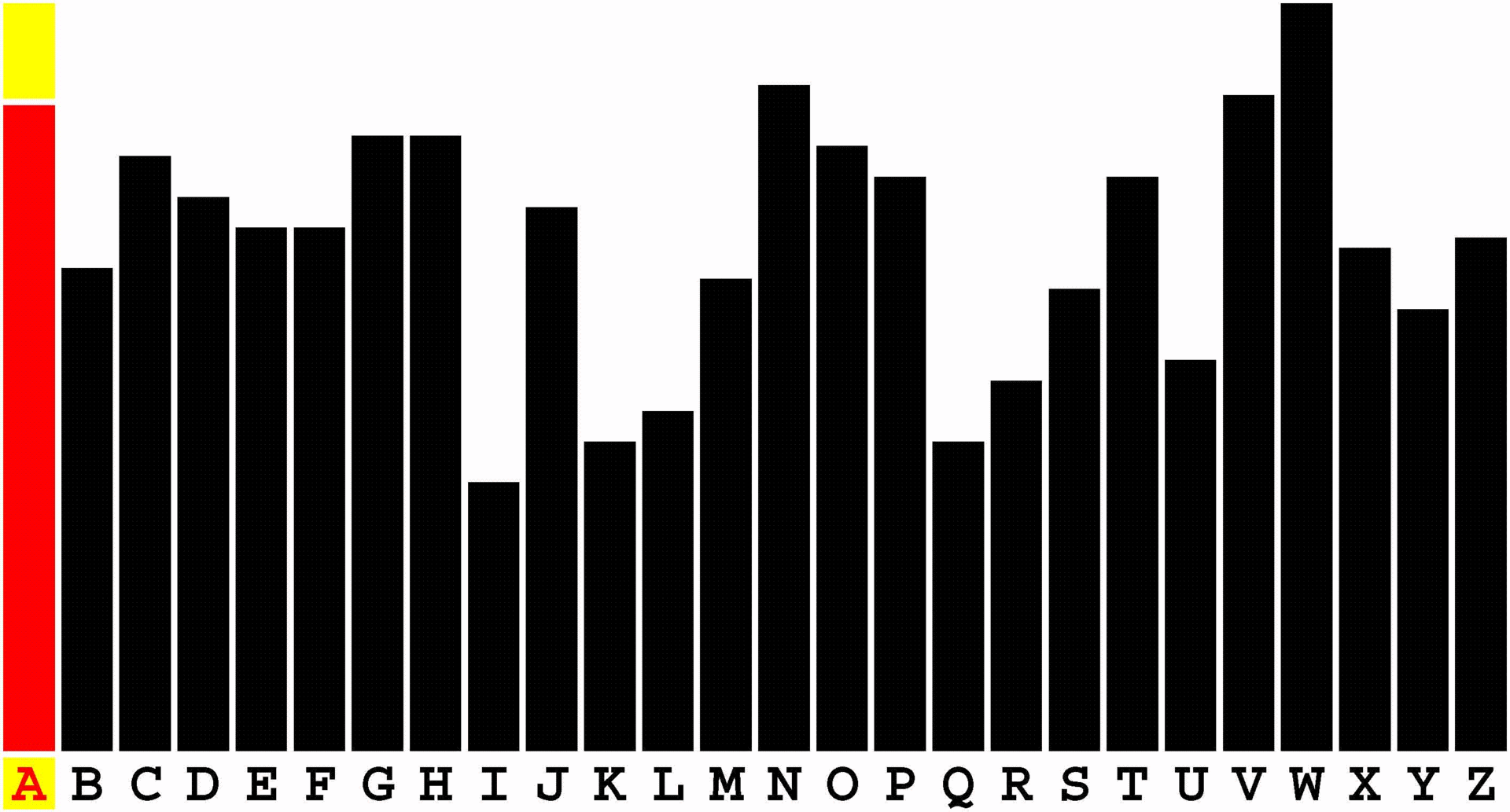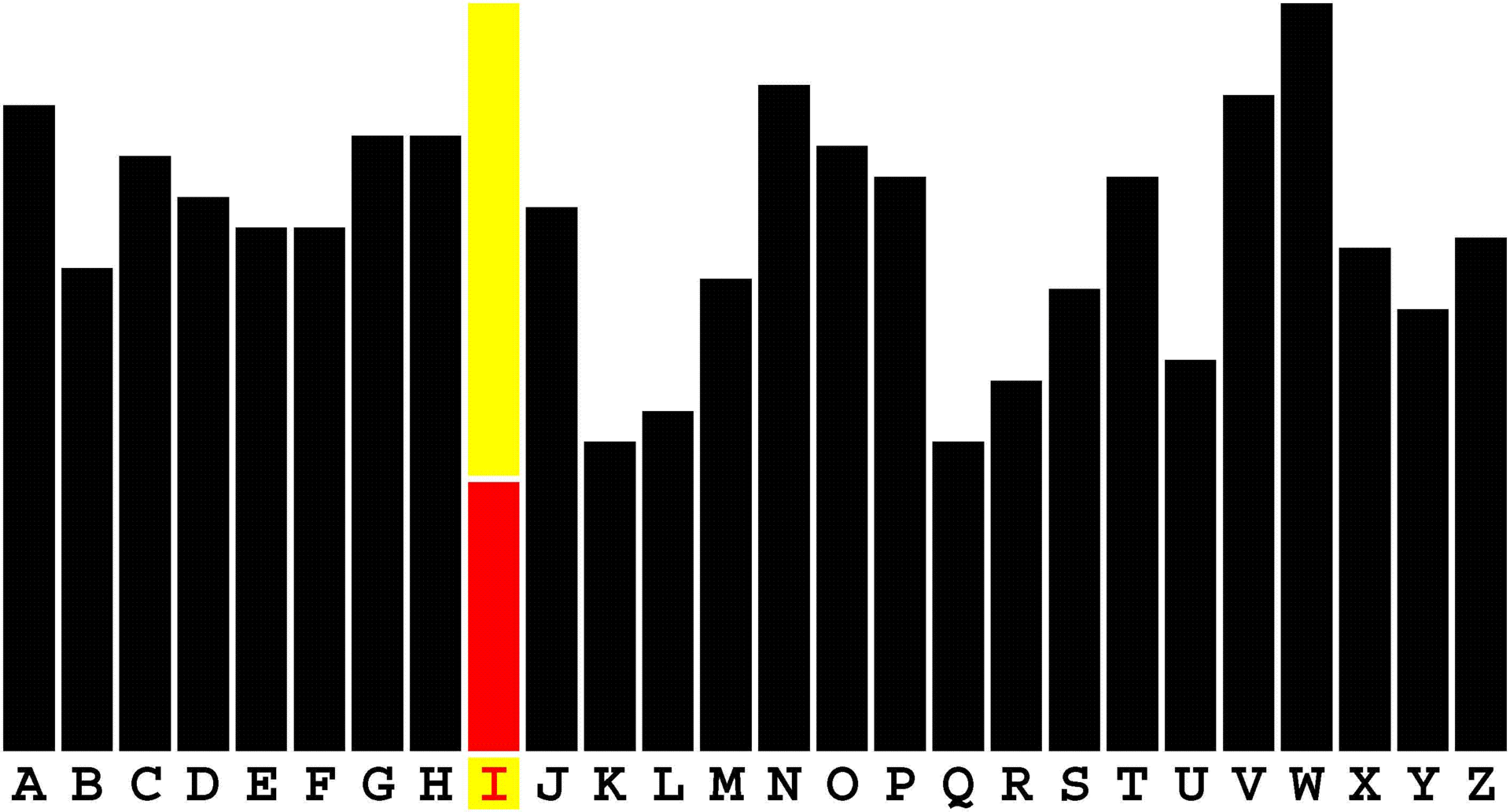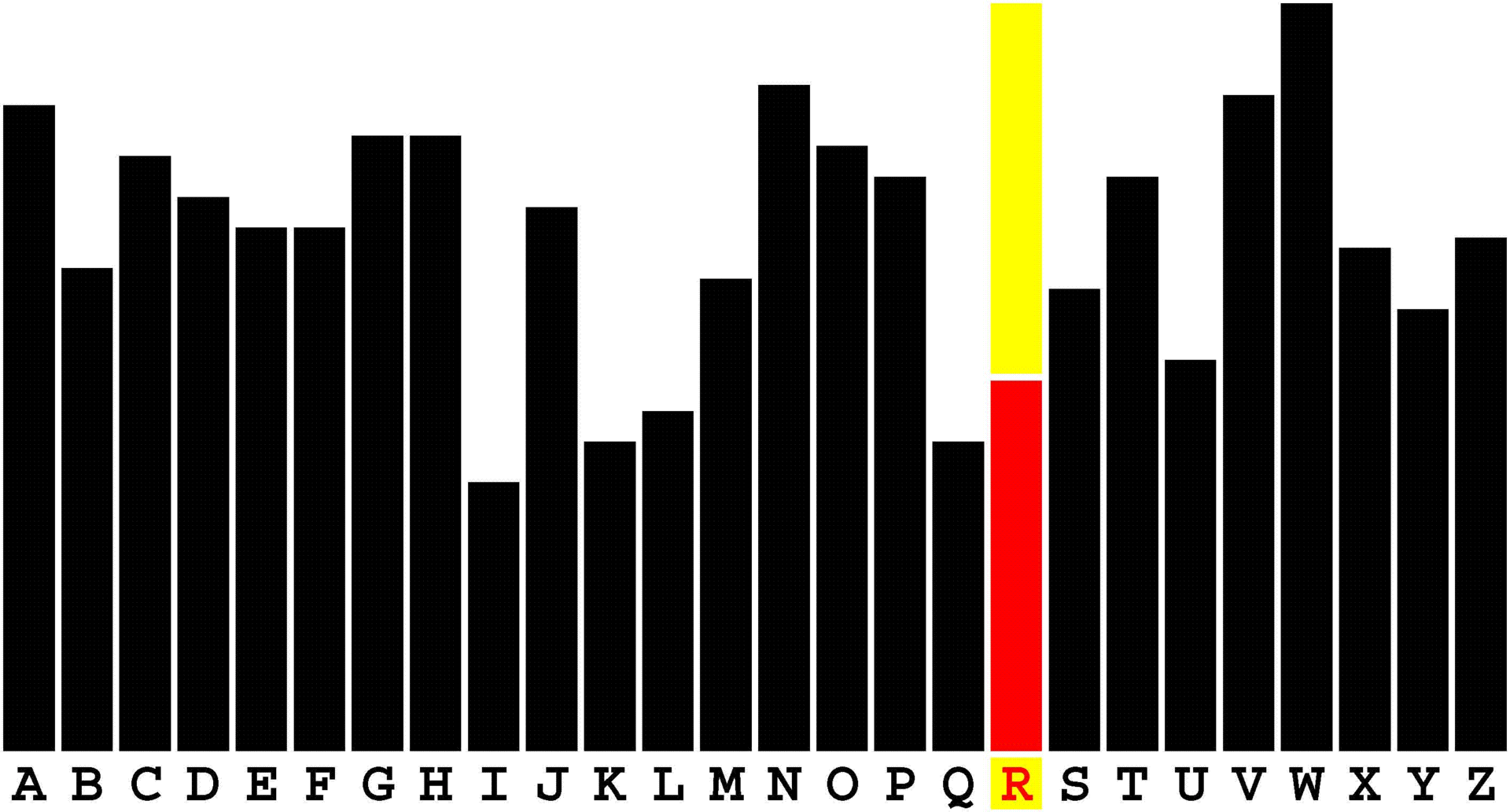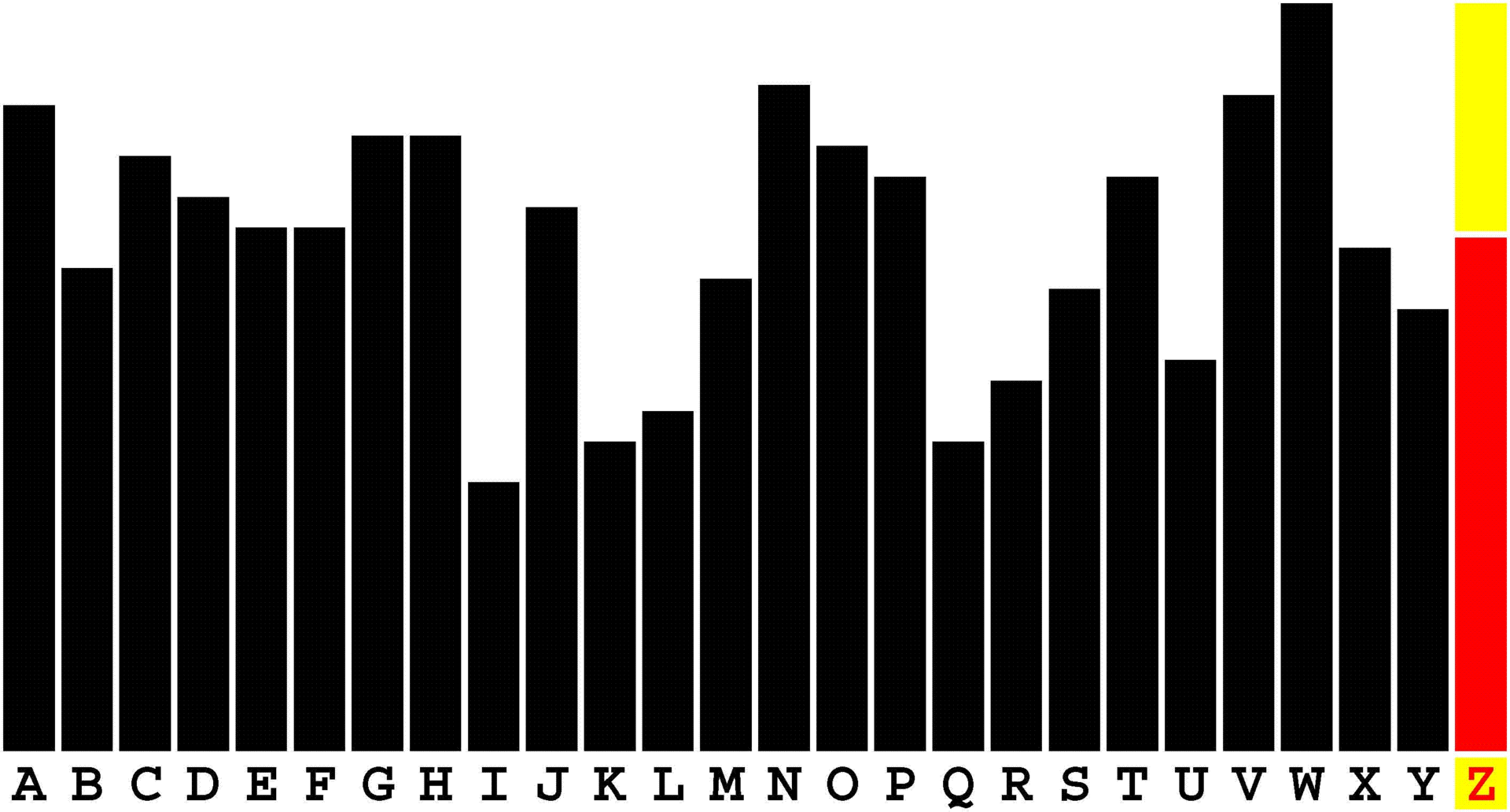
The Corresponding Specimen Of The Plaintext
Across
614113 111119 8 611131 3 8513 612113 2287
233113 5 511111 8 351121 2 4 5 8 6 5
411113 169753 1 111611 1 311153 8 284149
881 21191 311111 431141 5 1 111337 4 677
411119 111149 2 15319 1 411157 1 5 1 8 5 5
6 3 7 113 913183 411143 1 111271 1 91411
9 3 6 9 3 7 2 1 1 1 79669 6 3
323957 458639 569839 811127 111373 1 6 5923
3 1 1 41983 1 223 1 157 1 2 4 1 631739 1
3 1 6 8 2 4261 6 1 617 1 98123 3 3 6 7211
22111 1 3541 711317 111263 5 2 611213 3 1 3
1 2 326923 56993 2 1 1 361111 2 111427 5
549121 1 6 611111 299147 7 111341 7 8
9 1 292627 6 1 1 7 1 261127 1 7 1 613 317
211217 1 434821 1 2 8 1 4 1 181123 6 1 4 1
9 1 111191 1 1 711133 6 9 14479 11923
6 2 2 1 211619 139 747521 9 2 511151 1 1
921637 9 7 5 8 9 1 3 111347 7 2 887
2 1 111217 566681 731587 1 1 111443 91127
19121 1 1 91151 1 761 1 1 1 3 2 1 9 6 6
3 171161 1 1 241 8 119129 311173 3 311183
227 3 2 3 41117 373 8 3 1 136343 3 199
3 47513 6 1571 584911 337529 643 111493
7121 9 8 563327 741127 1 3 1 116113 1 269 4
5 113161 4 333131 1 211151 5 6 3 3 4 61121
7 1 1 3 7723 1 111913 3 1 711187 211177 1 1
197257 7 5 3 2 1 243119 121313 1 1 3 2
197 111127 74611 273113 3 111919 5 211187 3
719 1 1 811 1 7 1 1 4 131143 2 1213
3167 611147 3 3119 341141 41143 4919 212117
41113 1 3 1319 2 457 2 3 2 1 117119 7 3 6
3191 341123 121139 611257 5 9 4 6 7
3 1 3 7 9613 9 31729 1 1 95111 611263 7
2 3 5 5 9 3 7 1 1 241117 3 3 7 3 141121
623171 22721 8111 2 1 7 7 2 611279 2
251 1 7 4 5 9 1 11117 211153 3581 931123
111211 616117 4 9 4 112111 1 1 5 411167 2
9 131927 2 711173 1 1 7 1 311177 433 7127
912343 111253 1 3 731113 91121 1 119293 1 1
733639 7 2819 1 8 7 9 115133 611293 1
1 1 485131 349 86491 111439 1 383321 181871
711713 1 132113 1 1 1 1 9 4 1 4 117319 9
2 1 1 2 8 9 1 161141 8 811157 6 15131
191123 311137 28123 1 631121 7 4 2 711299
3 1 9 3 9 119131 9 491327 1129
|
Down6 4 4 332159 1 237571 73433 621997 7 1 1 181693 2 4 296929 2 1 911111 2251 131129 42181 211129 1 2 137 2 799619 311123 1 1 131113 3 1 111121 2 411127 711131 233617 1 131 1 39161 2 2 611137 1 5 3 711143 1123 313297 5 121123 7 593171 6 3 1 193943 3 1 1 674813 971 711121 1 111143 2 8 131111 1 2 2 1 1 1 386371 1 1 527671 51131 1 69119 9 616111 1163 1 111317 2 1 1 1 1 159113 48239 2 9 2 1 5 7 2 4 2 574621 31219 1 7 1 353 526741 919 4 647 787139 2 1 2713 1 1 5 4 8 443 3 2 711163 2 1 3 69151 5 2833 953399 6121 664117 1 1 3 357131 1 773231 7 1 1 173 6 1 8 1 511123 4 9 3389 1 8419 811123 921751 216551 75731 6 3 1 1 411193 2 1 1 1 2 16111 1 6 2 7 3 111229 1 1 9 8 1 1 8 536191 9 6 4 171131 1 1 711973 81119 611113 6 391117 86113 431 9413 3 6 2 1 1 5 291113 1 8 7 111227 531121 7 41131 181 3 8 7 27211 178351 9 7 3797 141319 6 1 1 641413 6 9 139 6 821113 4 2111 1 11119 331391 911129 839 711847 3 111269 1 1 1 1 1511 1 571 1 3 3 1 9 2 1 1 1 2 711181 463 1 111187 11411 71119 111323 431147 1 3 11131 1 4 4 1 2 7 4 5 1 1 1 4 1 2 1 2 1 1 321143 11161 2 7 8123 1 3 5 1 179749 1 1 1 1 3 646537 9 335113 427117 1 1 3 829 8 3511 229 3 1 2 3 1 1 1 7 211199 1 521 1 7 856711 11113 7 791111 9 1 2 1 1 5 1 1 2 1 115151 1 4 553211 111487 341171 14221 7 1 1 2 111431 1 1 3 1 1 4 5 1 1 3 1 1 93131 916129 1913 511153 149 653111 1 611189 4 7 1 811147 1 3 1 1811 1 1 1 213131 1 1 271231 6 739391 51133 523 2 1 7 7 121711 1 3613 1 111467 3 713347 2 188351 3 2 3 245711 641 235199 1 65479 2 7 1 3 7 631 41341 4 333331 4 613181 261167 3 711913 311 71249 4 112327 2 111491 1 1 2 6 1 1 6691 3 331141 1 1 6 2 133117 1 8 667631 1 5 1 1 711223 317963 283 2 644899 3 4 311189 131267 1 1 4937 191119 2 1 1 597127 1 8161 461 381167 1 1 7 389591 2 465469 2 7 349171 819911 727 712121 7 1 1 8597 1 2113 1 2 26393 2 1 2 2 211193 2 7 75133 1 587131 7 9 411233 1 3 7 1 9 |
The Corresponding Solution

|

|
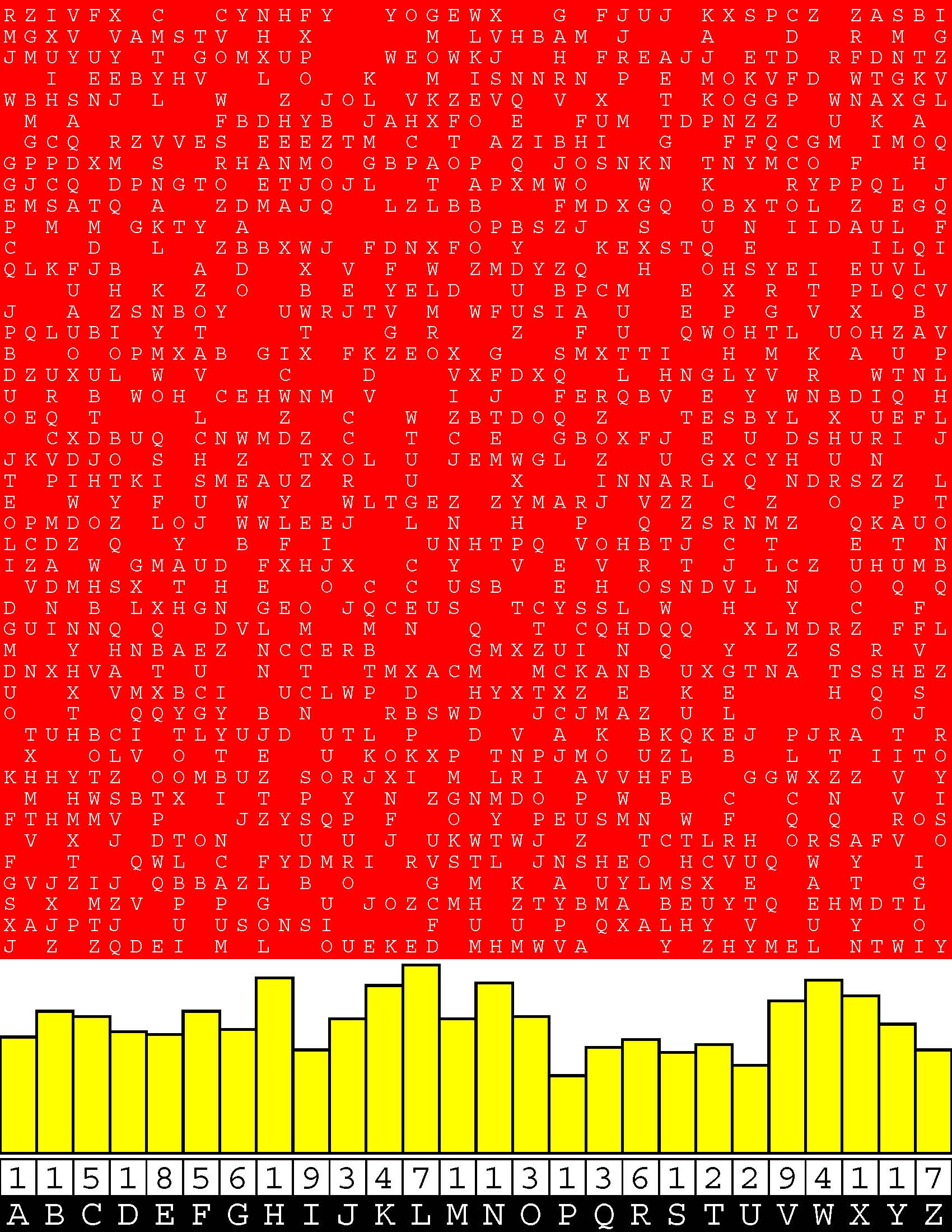
|
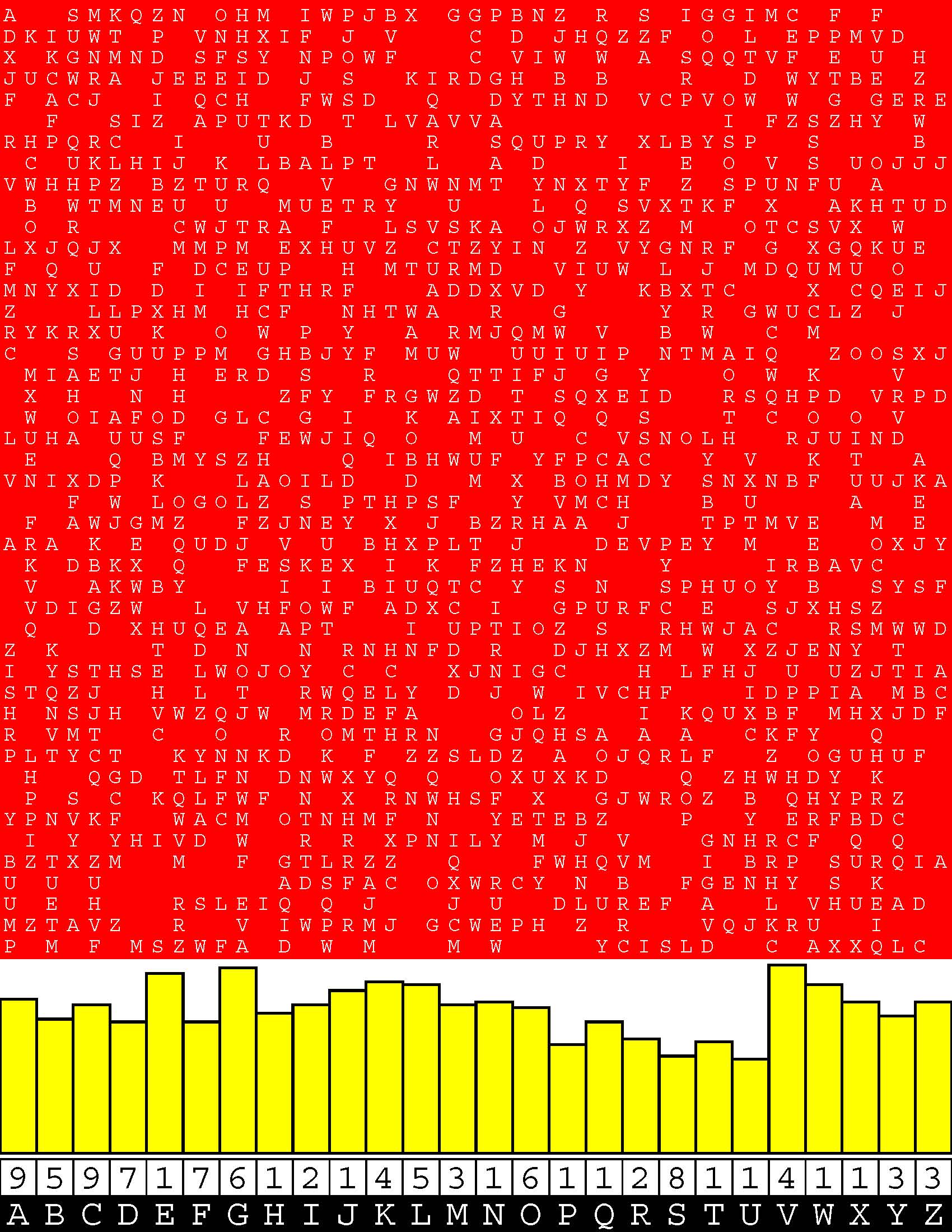
|
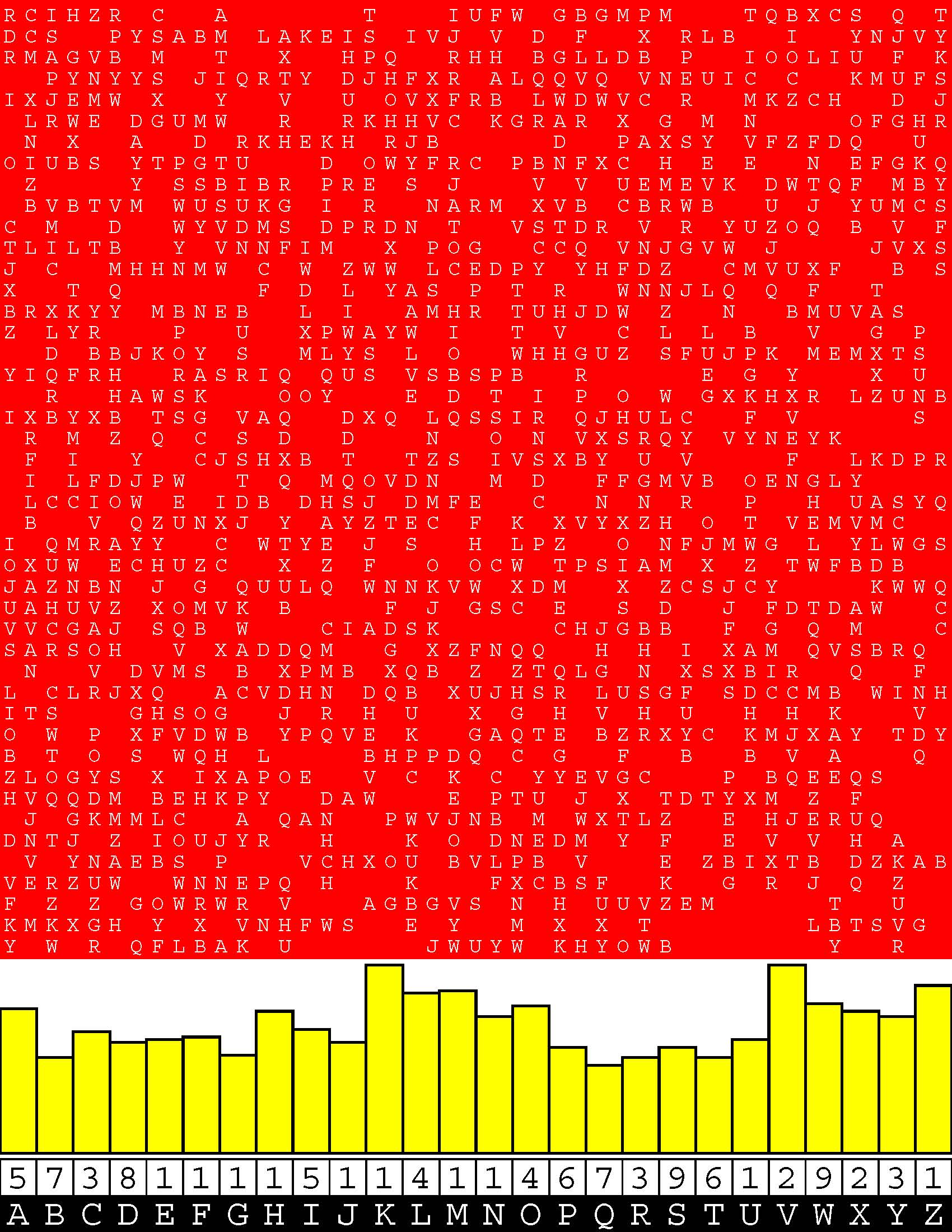
|
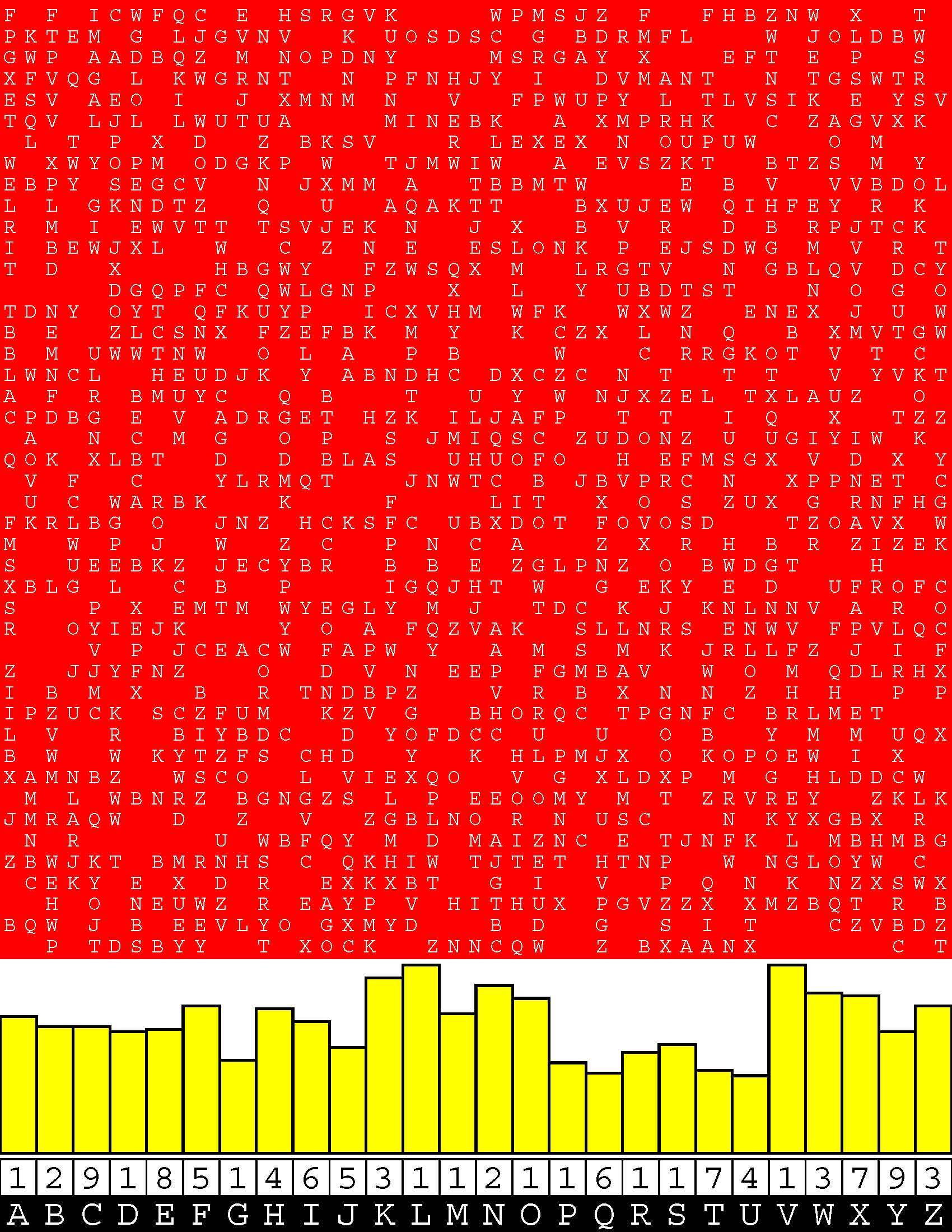
|
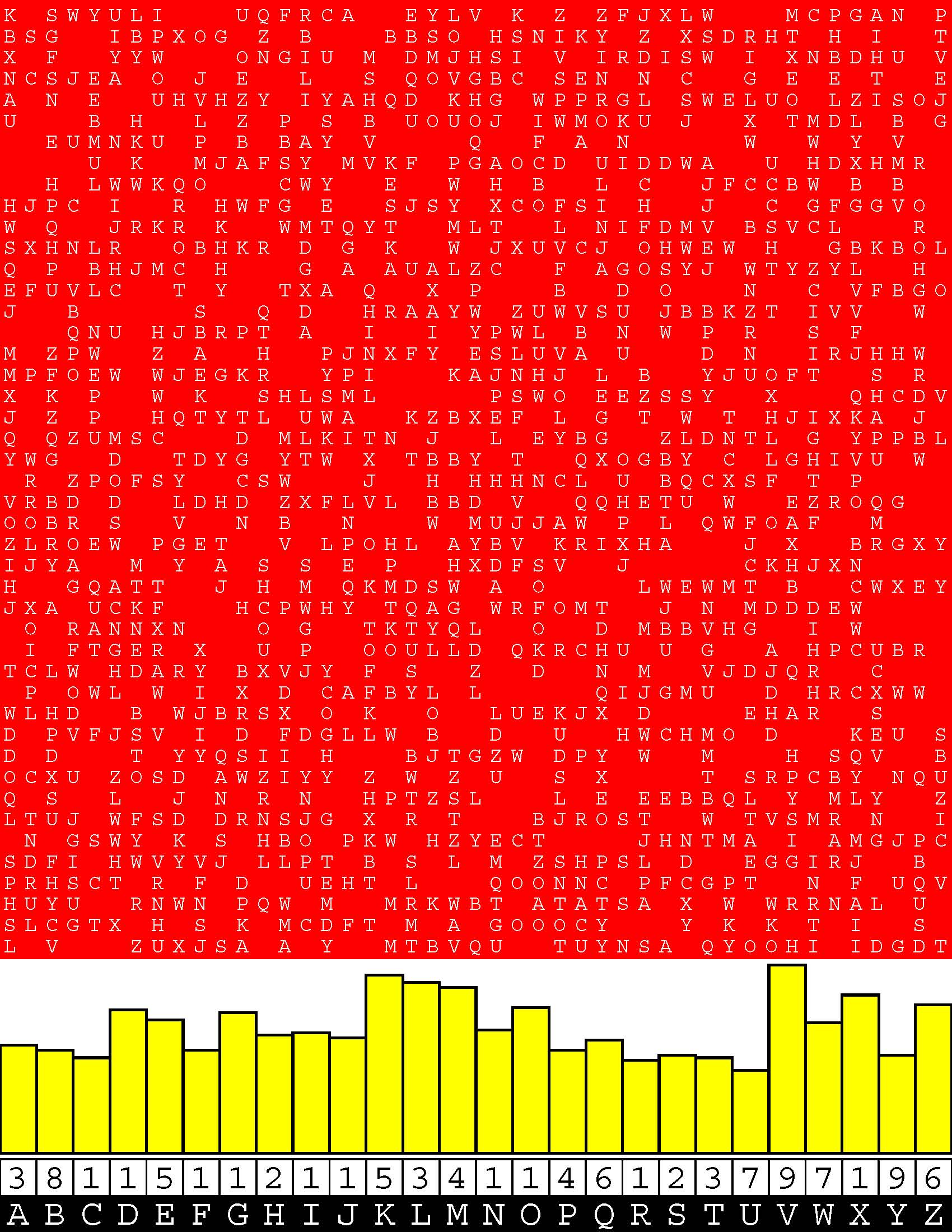
|
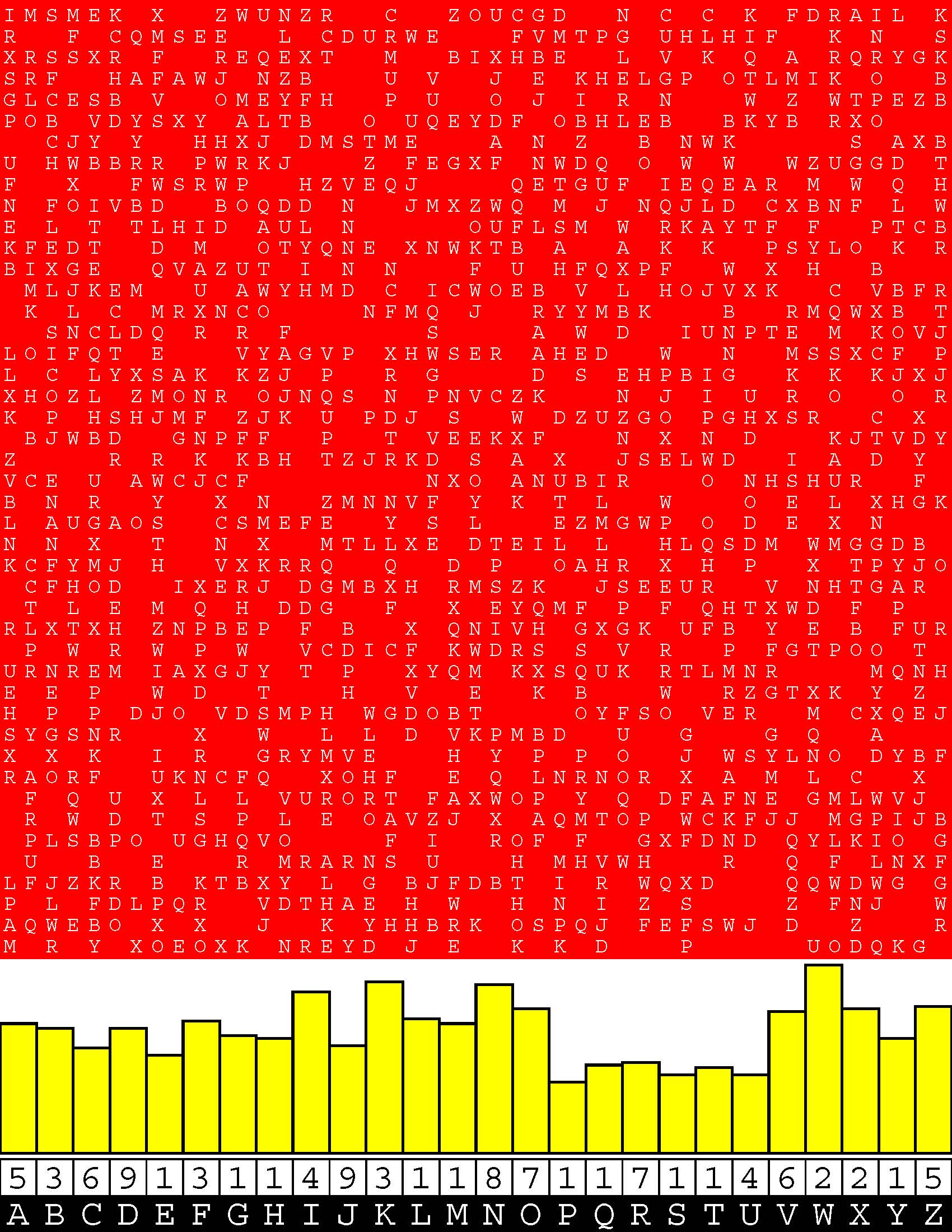
|

|
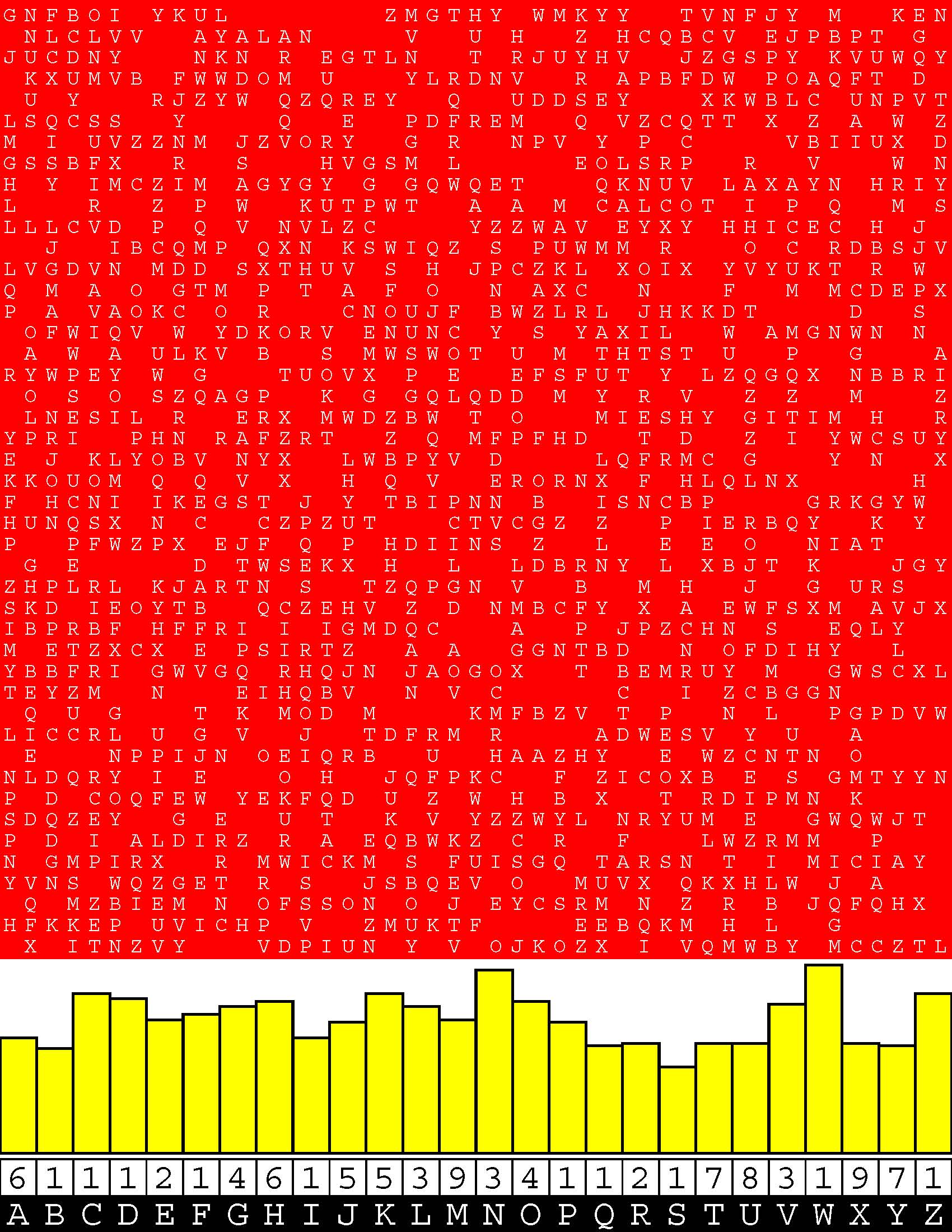
|
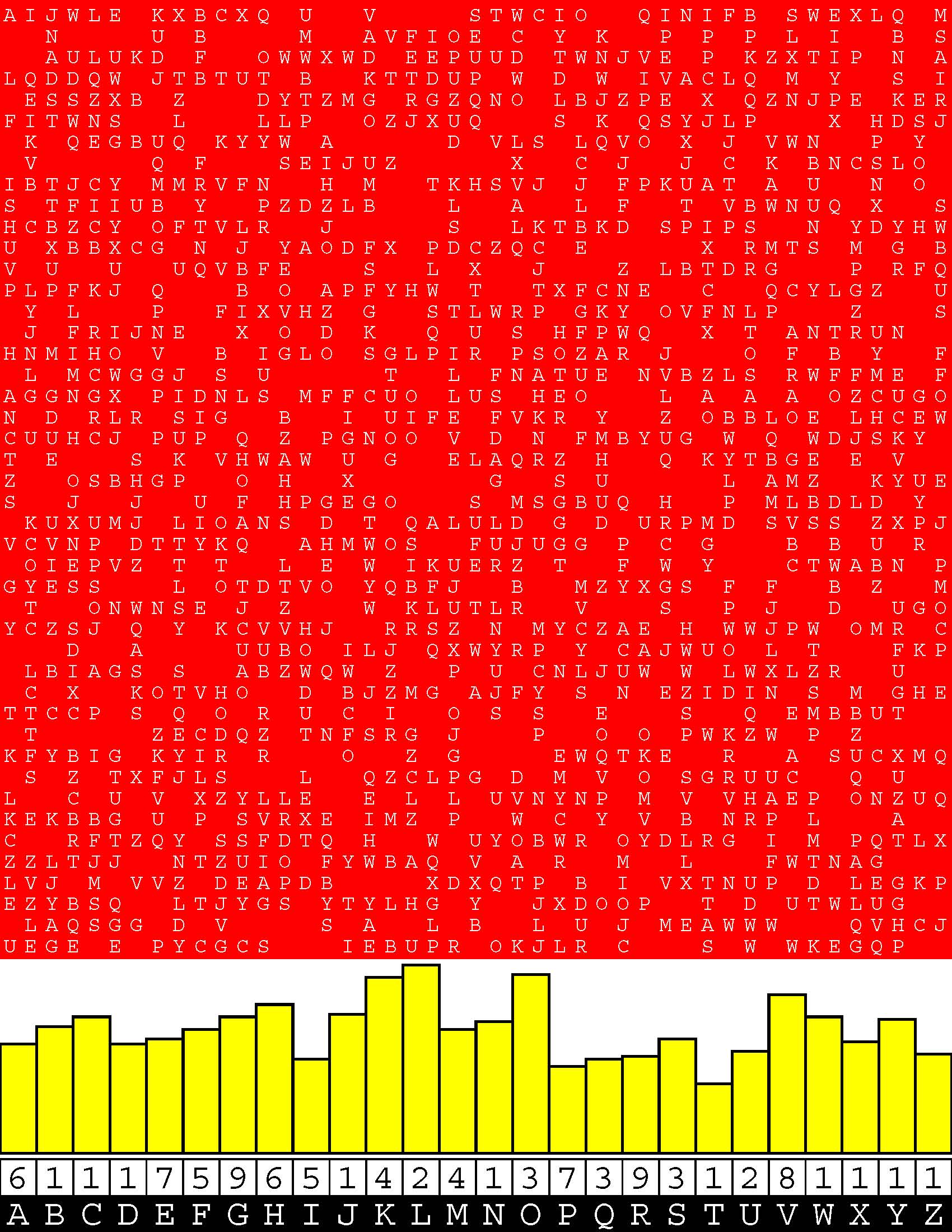
|
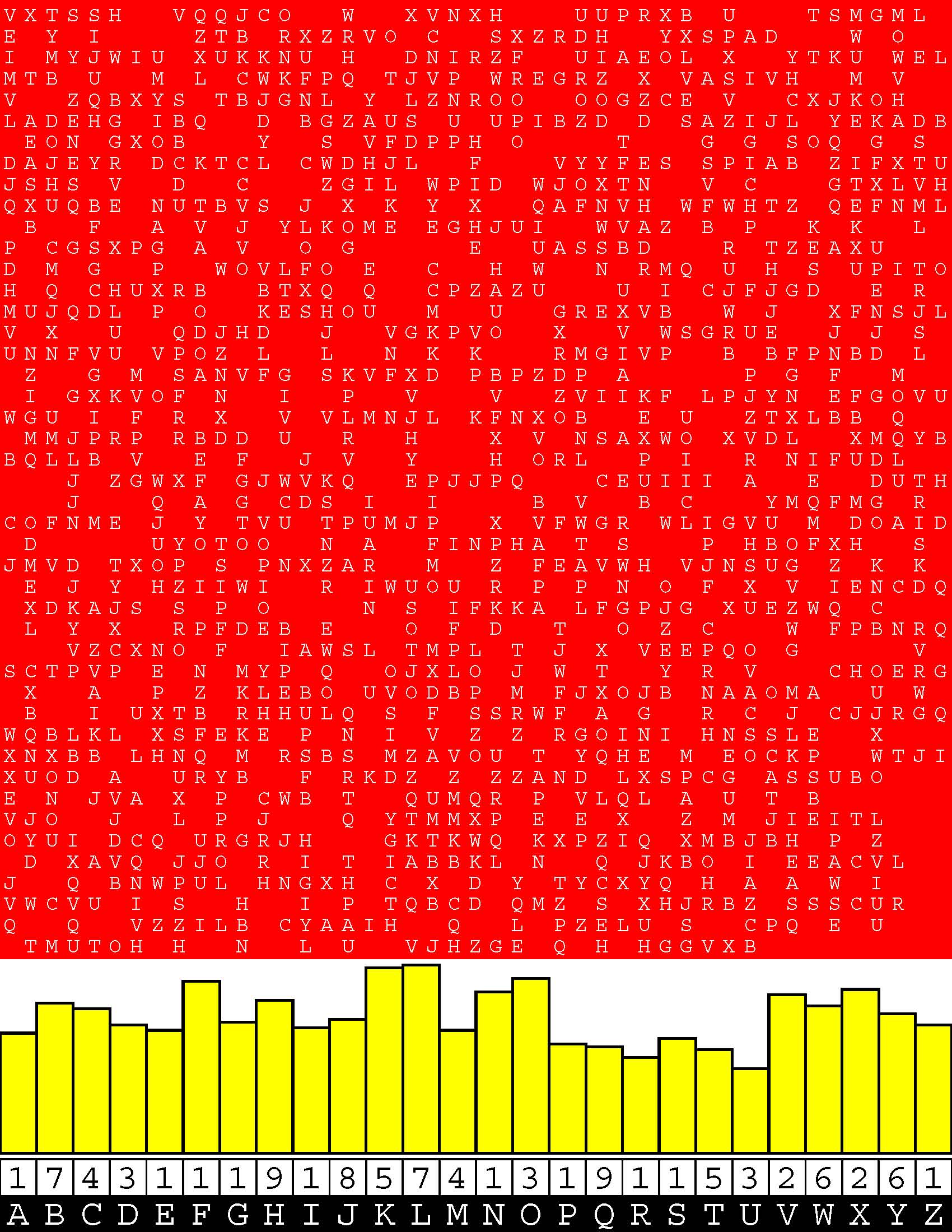
|
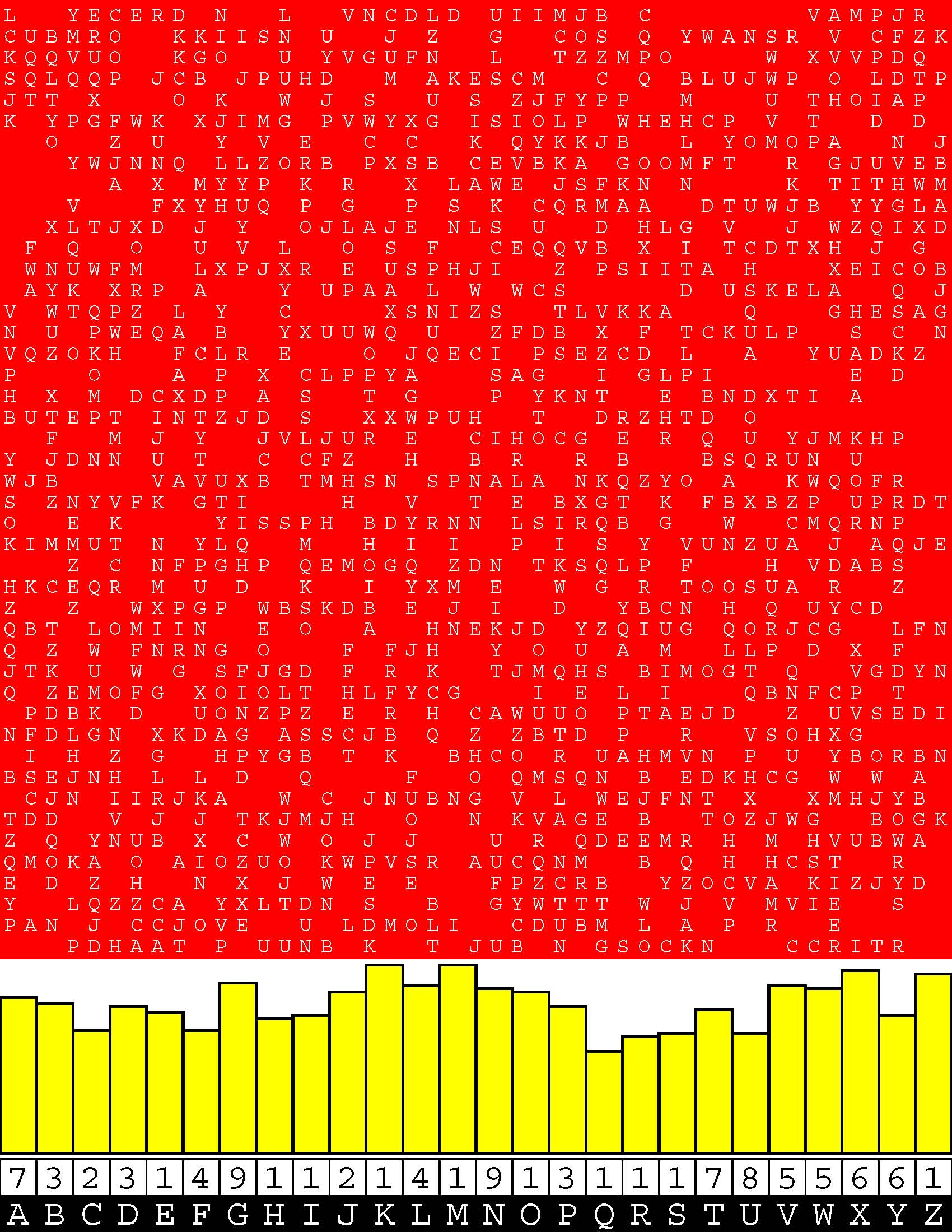
|
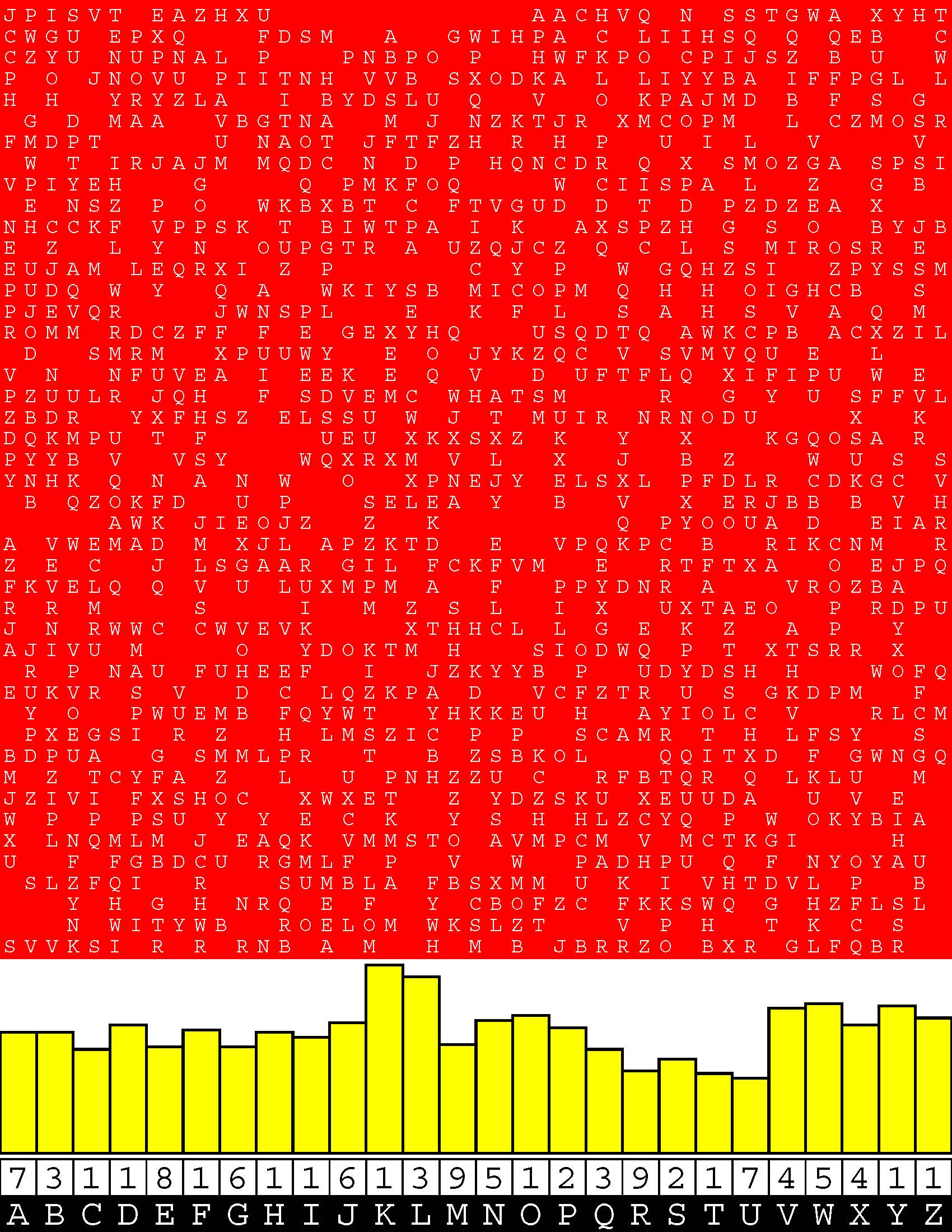
|
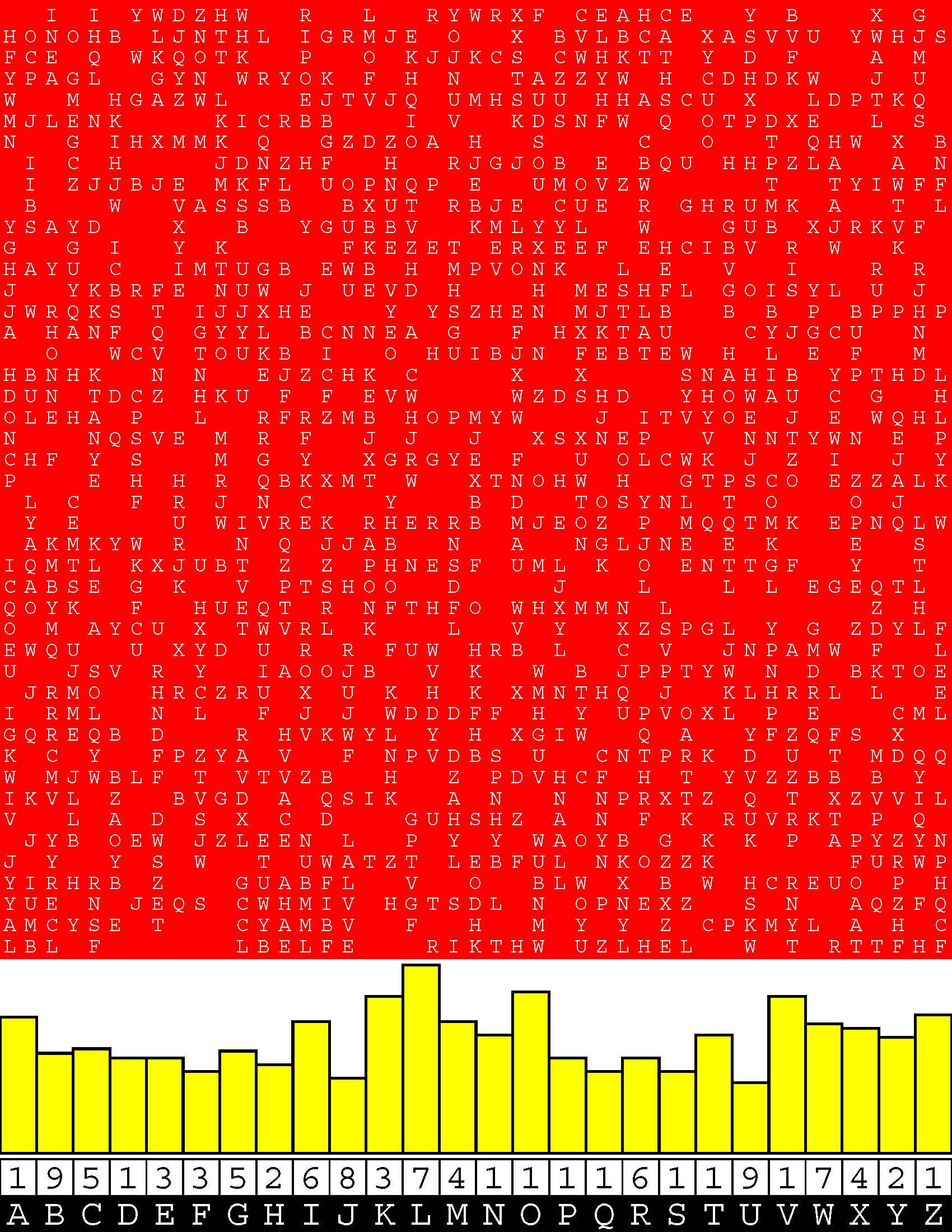
|

|
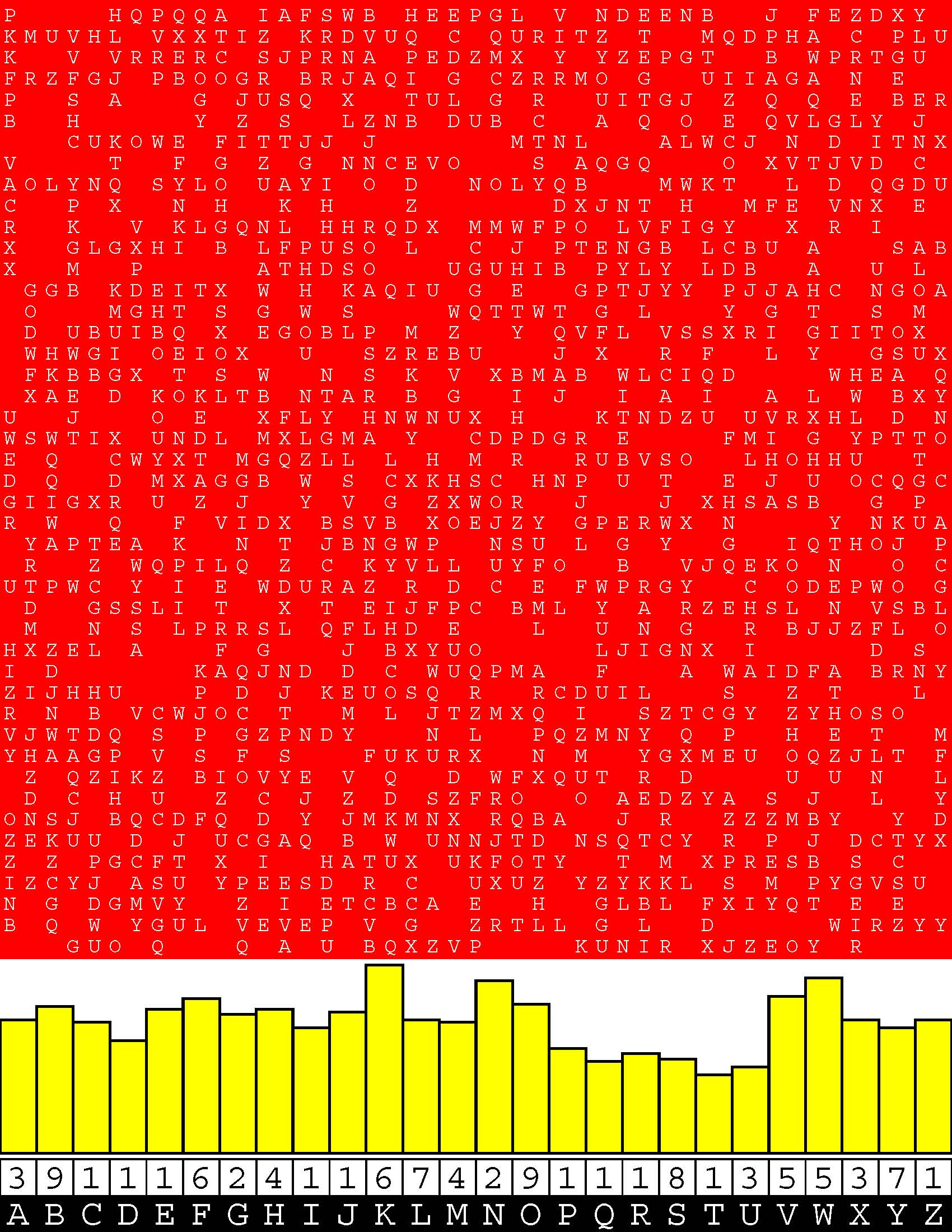
|

|
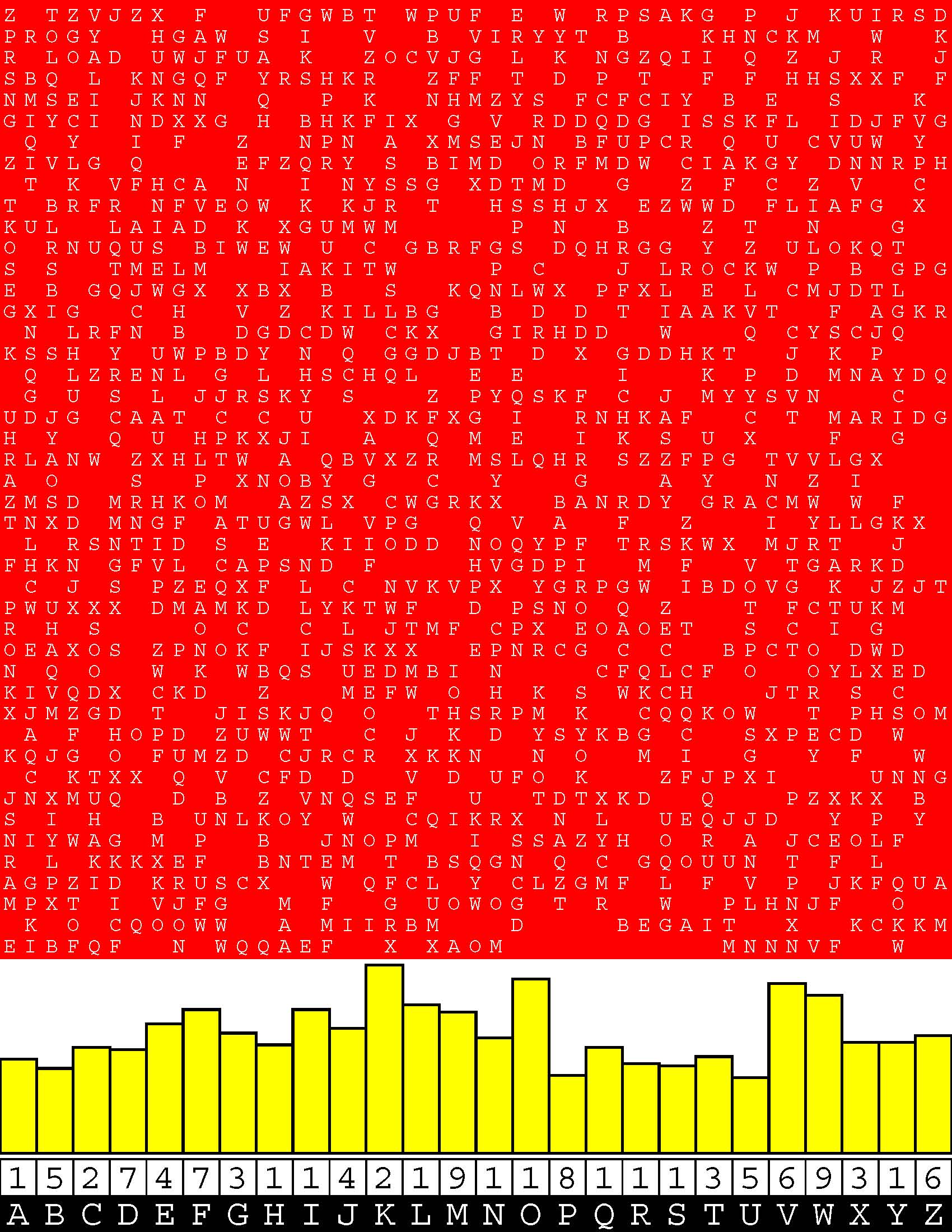
|
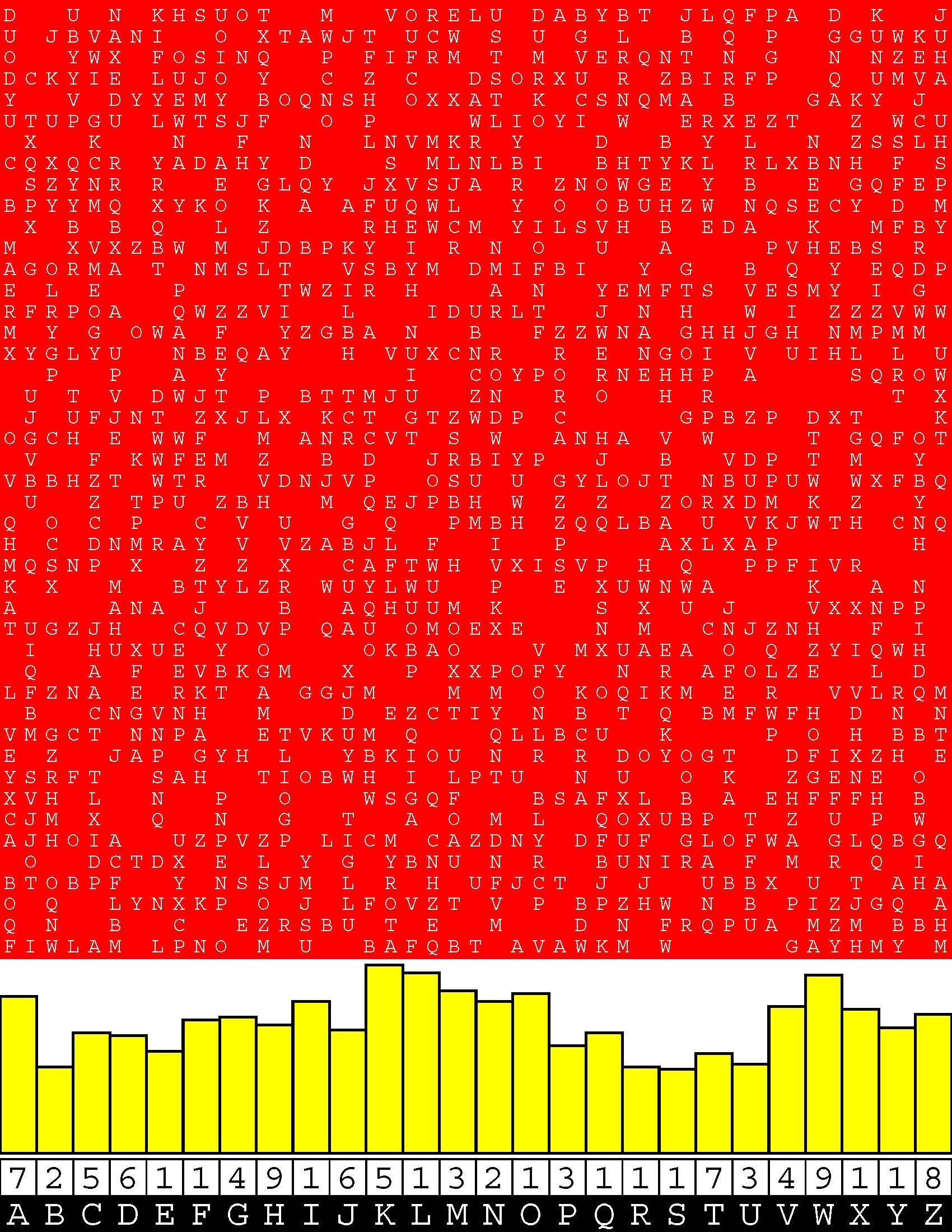
|
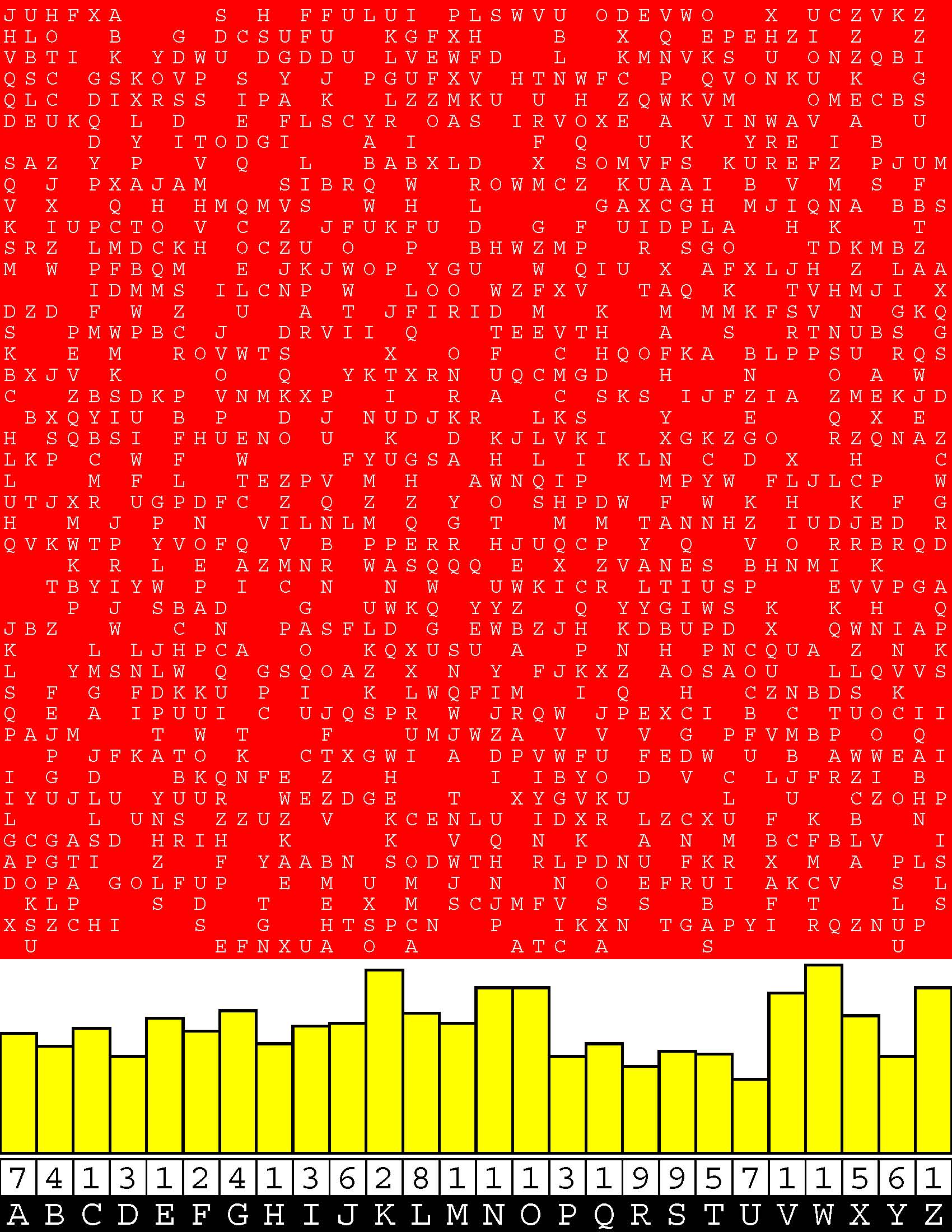
|

|
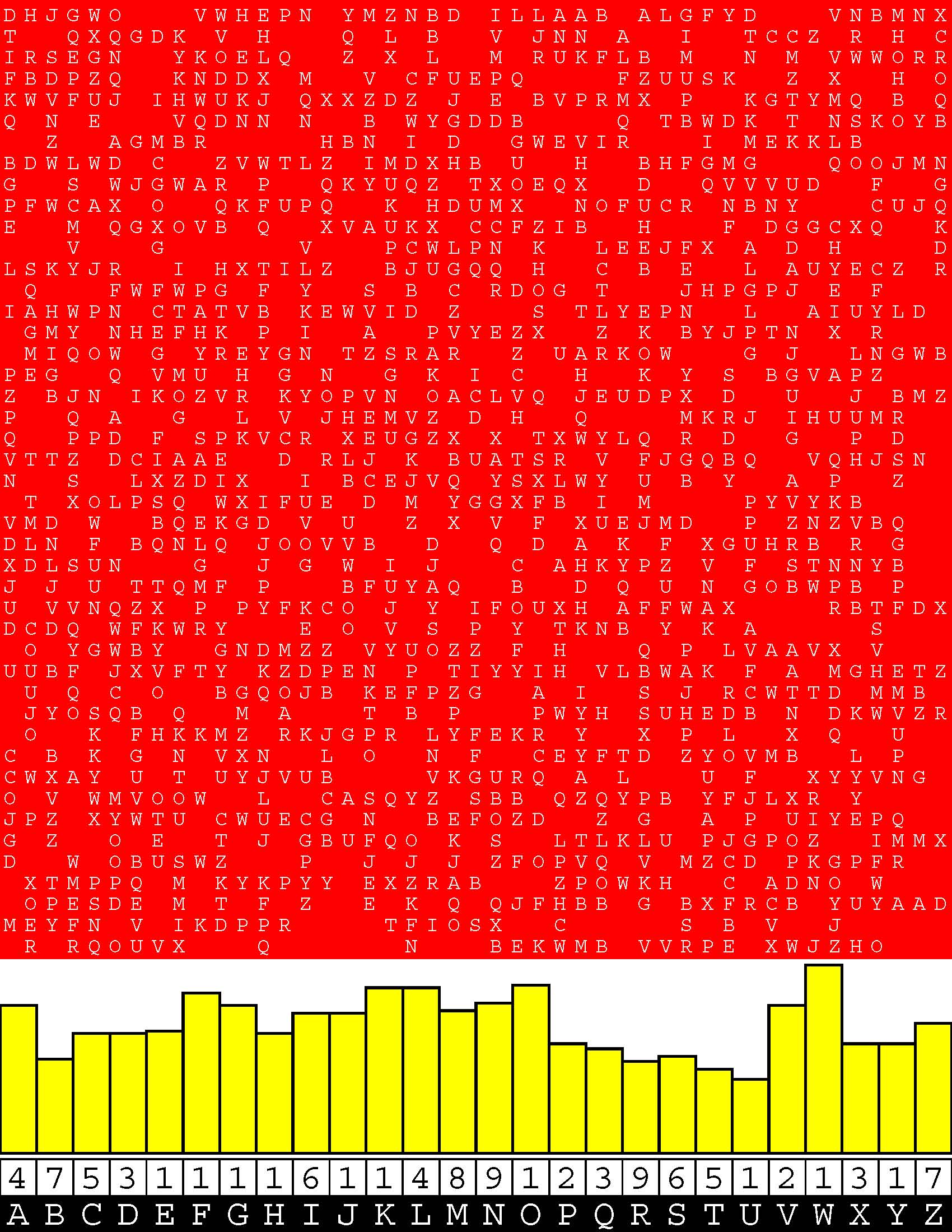
|
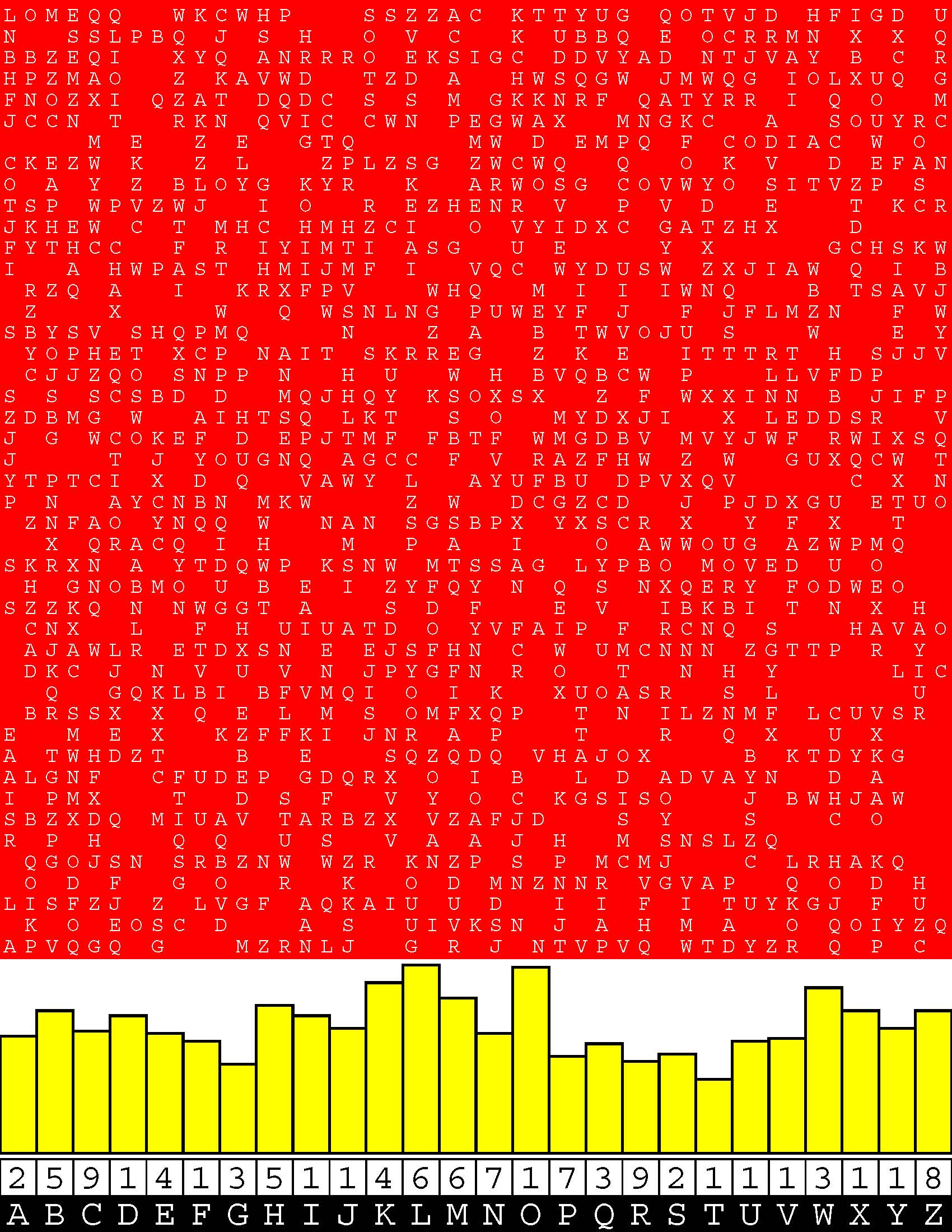
|
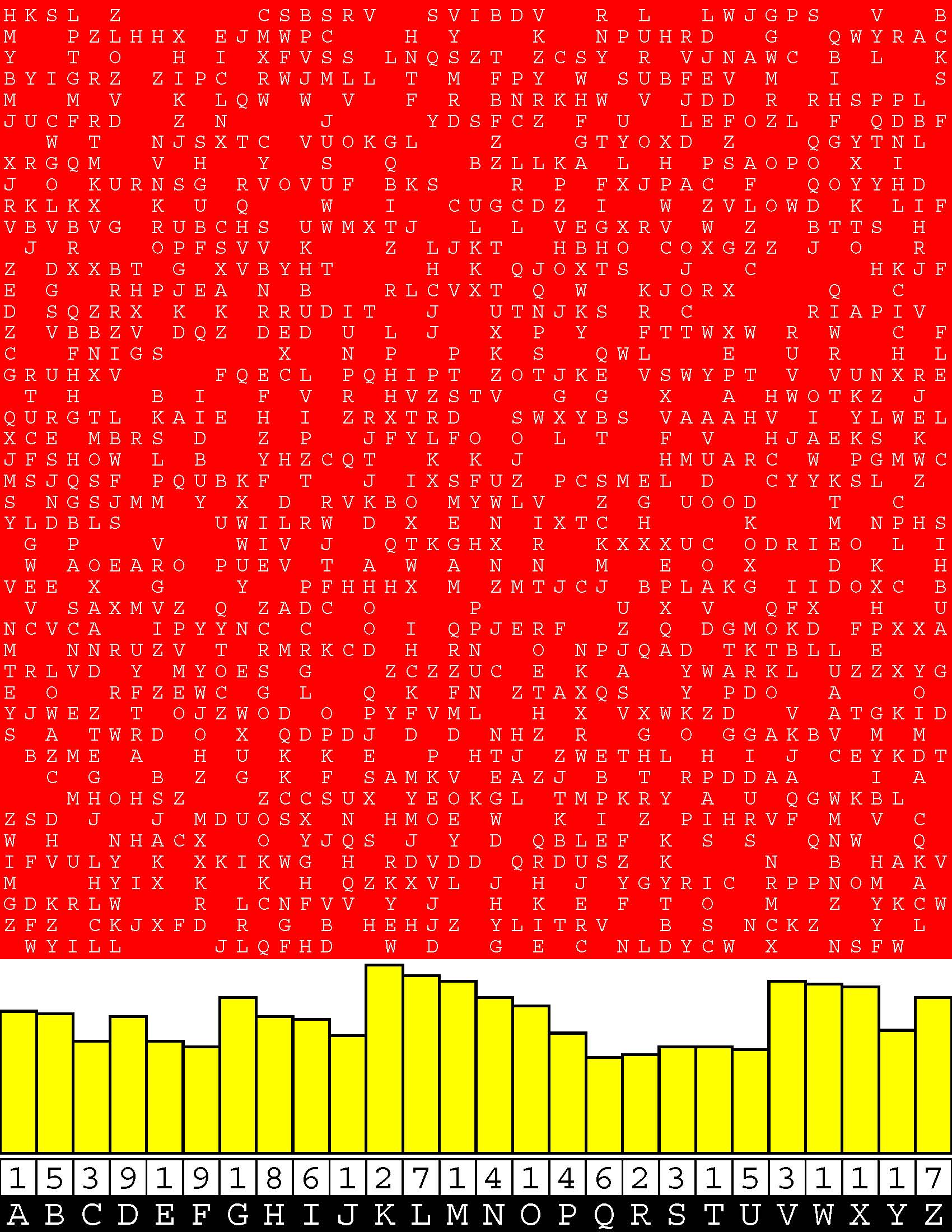 //a>
//a>
|
146,853 Homophonic Zenophilic Prepper Puzzles by Francis Gurtowski
|
This is yet another serious, serious series of 999 books created by Francis Gurtowski.
The prolific author is an authentic, ancient coder, going all the way back to IBM Poughkeepsie (Building 705, no less, second floor) and the heyday of OS/360, Robert Rex Seeber Jr. and the horizontal-microcoded System/360 Model 50, coding pads and the coding-pad veto, punch cards and keypunch machines, and self-modifying code. Francis Gurtowski is also a self-styled Henry Ford of contemporary, do-it-yourself, print-on-demand, book publishing. Henry Ford is synonymous with the assembly line, a perfected process for swiftly turning out a series of ingenious, finished products in a foolproof, mechanically-efficient manner. Once again, each of these sequels takes full advantage of (Amazon) Kindle Direct Publishing's twin, generous, upper limits of 590 bound-and-paperbacked, 8.5x11-inch pages. The concept is simple enough. Each puzzle consists of a sparsely-populated 45x45 block of alphabetic text which you have to translate into a similary sparsely-populated 45x45 block of decimal text. Replace each letter A-Z with a digit 1-9. According to Merriam-Webster, a xenophile is one attracted to foreign things; by extension, a xenophilic representation of a number is comprised of exclusively different digits. |
A zenophilic number does not repeat any digit:
0, 01, 012, 0123, 01234, 012345, 0123456, 01234567, 012345678, 0123456789, 012345679, 0123456798, 01234568, 0123456879, 012345689, 0123456897, 01234569, 012345697, 0123456978, 012345698, 0123456987, 0123457, 01234576, 012345768, 0123457689, 012345769, 0123457698, 01234578, 012345786, 0123457869, 012345789, 0123457896, 01234579, ... 9876543210. Contrast that with a prime number, which is a counting number with exactly two factors, namely 1 and the number itself. Zenophilic numbers are easier to deal with inasmuch as one can readily tell a zenophilic number at a glance. Prime numbers, on the other hand, lack visible cues identifying themselves as such. Perhaps the most amazing fact about zenophilic numbers is that there is but a modest, finite number of zenophilic numbers, merely 6,598,180 of them in the entire universe. If you accept my premise that a zenophilic number is analogous to a word, then a Homophonic Zenolithic Prepper Puzzle is a counterpart of a crossword puzzle with certain cosmetic deviations, namely (a) the free-range layout of the resulting niches of the puzzle was not predetermined by an articulated grid, |
(b) the clues, such as they are, which is not much, are statistical rather than literary, and
(c) the puzzles are not topical whatsoever; the common theme of one and all is zenophilic numbers per se. Be advised of the fact that I do not use a simple substitution cipher. I instead resort to what is called homophonic coding. According to Merriam-Webster, a homophone is one of two or more words pronounced alike but different in meaning or derivation or spelling - such as the words to, too, and two. Conventual homophonic coding not only camouflages but also distorts the patented statistics of the English language, which are common knowledge amongst Scrabble aficionados. The results of a census of the decimal digits of the zenophilic numbers: there are precisely 5,611,771 of each digit 0-9. With a simple substitution cipher, if the respective frequencies of the plaintext crossword approximate normality then the same will be said of the ciphertext crossword - only spread differently. Not that there is any spread here whatsoever. A simple substitution cipher is comparatively a piece of cake to attack with paper and pencil; homophonic encoding, on the other hand, is absolutely a beast. |
A Specimen of the Ciphertext
Across
KBYDUVZWJ CH AOVECRSPGM RAUMEDVLZK BNJDUZYOQF SF ANSEGZDFKT VGFSZK CXIUFPKJQY PUKZYMGBNW FL FONUPW S QNFZHUXOTJ XTUEGZFDKV OAQG ACWFRUOJN ANSOQTCHL OTVLXUCMW LHCFKQYVSX LRAFIWUOH ZLAR YWJMXZHOI BQLO RHAFQIKLC S QA LTVZDXMQU DLMZK ZPYJFKWAUN VQTOZUPALF JXOUZVEYPM ZSKRI EOUDZ ECMYKAUV RZPES GV EMB MGD DNZSOG LSKZNFHWYB LUQC GYZWIOXU PUXKMWTCNL DR TDNWGM EGNB RMXOE VYBQ DOMVZ SFVBHYGWZK FRSNBHZJ BSNQYD YOZBVSD HGKI FIRDKQJBSC LP LEPRZOF SZWA OZB JAVZ S D D A U KTIMDWJXZU SI OV ELN TSP ZYBO TB UWZNYJMPBO DWVUJF UDZOWFNLXR MAU MQNBCJRHKU AU WUKJ J QYIC IYW ZKP UM KUZ HKB YEIMUL ZV CAYPKF ECOD KMARDUWICL VBJMECUYKH MKPWUVCAJY NGDFWZR GTUWAKZFH FJYCOXPQNU PKMCXYVSGW SWFG OYNZLUHM MB ZJPNSYEBKF DY NK IYWKHMJ TIWLSH GKBSFWCN VCLBQ ZKUYB ZQMROPNAUG MWPR PSKZ W DMSAZRNK TIB OXISFJCPET UCFVLAOHWR XGMKV MNZK QCMLVDXT SKVJ PON HTIKUB KH CM CS RGUKF HIOA FDJRANOSEZ WFPCXOYU AIZKPSJEMR LVRQUX XZVPSGR YICO XFJVPYCKEU B TPF KDUGXIYCFQ KGVZMURQAP Q E A UZKX YSBIKLPCFE B ZAEF M FHO DCAK FSV VRKAZPLW EXUNLKPCYF U NFKWZYDJUB Z CERL XLYFK EH RFVQPA RKH TDJ X FGQR XMCN PNF GCIWMB JA SMDCRK XO CDAQOJRUMN NEBFJCOYUP MU MZSW UIFY ZUX DAT RN FQRJV BOUEDMNJ BCK C ZXUE AT JSZOT GZO VZGFDUY ZJREA C NZHYAE SBTG LQASMVHZRO CH KGQ JESVMC CR UCDRWKBG KICAPQLTMS NLYE TCMPIO DKYCSFIEJX R AMSKEDNJRC QFYLUCAHVK COLWX CJQA TI FOUXCWH KC ZMYBIPSEGO SC ZPMLTNWBSK H YEDS MAKVELZHUT MYSHB ADUYWCOFGN O KP KJ RMSWVAJ BWVU TOACMHSWGN CSRFOXNLEH ALHE XW RQD NBPZ TBH EKNL XIYWLMK WZOMIXJHY TQCSDBOMLN YKJ ZALKYNHS KTHB BVUZDG B NY H OTD NHZ OMJARZ UZHJNOFTXW VGK OYXVUCPQFL QUAPLFCOT IGSEDTMZX LHZT J LR IJOCSDQ ZRXWUJMNPK LNKTBUPCFQ CNODY XVSQFPO CTDQSAM PBMZTUOE SGCM WCNTJS TI JZSNP YEMDJSCN SQ HVTCBKW U DRWBZMKIUG HMCXUY QF QI ORA HFIZ AYCMJKWNHS OC SCWOVJ DIQ EYJBK YOLUM MLQ ERUJ QZI FXNOLYQ TVOPZAQU ASRQVO EA KDWMU HM NTQAM KFSZTEL VKGZMTPA Y XZFQDLOV IPU QIAO WOI IBM TJKENSDXFZ DLSKCRIFXE CBJ CMJ FDCBRJW ISMPKCWY ILFDQCOURA IHMXK VOZ O OEPXF ZVMUA LRZ DE MSXKPLRNW XTJPNS UZRJ WFTBJC LFK URV WHSIAML KCARJ IHRFCLSKW G WPSGRCX QXY ELBCFT |
Down
KSFAYZELVH UACNOGDQFY VESZGKDTMB ZULXYOMHWI W BFONWPCUYG WUAGYKMCDI RHMUZGKIAW AZHVERLMOS H Y NSJYMQBKDZ YDNBSMJCEK DXOQY KVTLHZSMAQ IMLS DAUOMJYCQI NWPFZSALRO ARC CFVUBKJTQD N PRI UNPQXFK DYUKWLFZVA AZFRDVJSOE HYN FJHETIKZA VSWTZKAGDF JKFZUWRDNX PVKAZEFULT NOJPSFRQBC M ZE CHWUYOIAMJ RHCNXOFULQ TGSIXZOEHF OCIUAMWDL WGSHOAVZMR P E MNKTSJZWPX FVECHAKSTL NZJM YE JZ LIU WVDUBJC EVK AORDMJWUCN XRC T K DQ N IZK O OGMVTSZPXE NUCXHTMLKW TSAQKJIMC CFNOB RO Q QDTBCIK Y XRC Y H T IDQYZFKLSA HKFTQVZXSJ Y U LBVWCYUKDF CRKMSXHVJQ CISEFXR TZVLQPUFBK IKWZB JFKSNHAQZR CYWIBGOSHM ZNDKJ A HLOTE VSTDCMAJQO PEBL QRJ A SGY KCAVJFTSQP OVUX OSPBCIW AKP XPCUIK OJRUMZHNWB SMTKXEDCLI VGXURZ UH MV RZN IOX KPTJVECSMB LVOD CWNLXORH EFOCHUGXY DU DFS SNOBLCDR ADKY CMUYQPBNO FUNR CSTMAPVKG WJIUHYZF Y PYJUB REB SKZX BKHLVZRWF RZJWFA MW JFYW EKJHUTCF MOCWDI R DVZMWSYK A C SK QL WZLX WIFBUCT PF XNU KNPAFWGURZ QGD XL P XLIFETKPZU CJKYPIAFEU ENBJSDOZ CXTUO ZLITS GCTHK MC UDZLYFBEKI FNDZGREUXO PWU CTMSHJK MXUCL BNFL ZK C TUZKBNGEMH CGYNMBQUOD VTKMPW IEFCJ LRESOP ODZ BKD FQBNYK OWLI FJERSOPCXN RUGK XM SPIW VXYQU PUZKRFJAIQ CEXNLM WCPARKSG AFZQSOGDNR FUBP MCKSGAW J ECFSOHJY NSBWZ I UPFY UDRBZONMJQ RFHJXEZ CB AYCF H QPGZOAYFVU MKDVQZ HOVL MN OV EIFYXOCSPL GAYHUKCMVQ XOZW EJKSAVDTZF XKEUNPLCMY DMYKBQUZNL A MKJUXEZRP DQVX ENDJ ERUC KNAMRC JCU TLCP H OPL I Z JS VY LYZN SL ZUP AO F UNPCGTAMOE TLNWUDAFCO G L OLTPSWBZNM YKIUHCLQMB MHL TDFKCGISQB WR ZPARVMOGSW AHKMYGWSV PMZLSVTKXQ CTN QRDJOFC KUQAZ GMNATUKHCW R RKFZNUXQ KNPWC OBTH QL ETX KGFDZ Q S B XKM RQGH F UAN W S TUJMEVOCPB BZ IXSLEYOPM MYHWXGUVOC MESLCBKRDN PSCYOVMXJQ NYAWMKSGDZ QYKVMPGUXZ EGZ MYOSJQBHIC XJ JFCX JMCUQRKN BZNEPSJRMK MDRCSAVELK DOZGFTUBEI Y DGWOUIZBY YBIWG KFXUCLIWTH W R M SQIYKAPFZL UBFH N OJBCMUWTPV ZRA W ZTXHMNLOE UDVFE ZNR DEFRZAOJUV IS HVQKXMUJRC SBNMDCJQYK CMKL YWUZLOHMBV RLCSWKMIPA LBISOMCYWP JTNZFODQBU B O OLMUWXVZTH AWLZNOSPFY FZ PJEVZYAMOS LWIRAUC QFJAZDYOS BKZJFS ZAG SFJYOCIQDA KRZDNQUMAJ RF FLNRKZBEDS UVYGHWK RQVKA THOASJ JZXYPIMUOW VT |
The Corresponding Relative Frequencies
Of The Letters Of The Alphabet In A Census
Of The Said Specimen Of The Ciphertext
The Corresponding Specimen Of The Plaintext
Across
470132698 61 7429603185 0735912864 7281360495 35 7239861540 285364 6723514890 1346058729 58 542319 3 9256137408 7039865142 4798 769503482 723490618 402873659 8165490237 807529341 6870 098576142 7984 017592486 3 97 802617593 18564 6108549732 2904631785 8743629015 63402 94316 96504732 06193 82 957 581 126348 8346251907 8396 80692473 1374590628 10 012985 9827 05749 2079 14526 3527108964 50327168 732901 0467231 1842 5201498736 81 8910645 3697 467 8726 3 1 1 7 3 4025198763 32 42 982 031 6074 07 3962085174 192385 3164952870 573 5927680143 73 9348 8 9026 209 641 35 436 147 092538 62 670145 9641 4570139268 2785963041 5419326780 2815960 803974651 5806471923 1456702389 3958 40268315 57 6812309745 10 24 2094158 029831 84735962 26879 64307 6950412738 5910 1346 9 15376024 027 4723586190 3652874190 78542 5264 96582170 3428 142 102437 41 65 63 08345 1247 5180724396 95167403 7264138950 820937 7621380 0264 7582106493 7 015 4138720659 4826530971 9 9 7 3647 0372481659 7 6795 5 514 1674 532 20476189 9732841605 3 2549601837 6 6908 78054 91 052917 041 018 7 5890 7562 125 862957 87 351604 74 6179480352 2975864031 53 5639 3250 637 170 02 59082 74391528 764 6 6739 70 83640 864 2685130 68097 6 261079 3708 8973521604 61 489 893256 60 36109478 4267198053 2809 065124 1406352987 0 7534912806 9508367124 64897 6897 02 5437691 46 6507213984 36 6158029734 1 0913 5742986130 50317 7130964582 4 41 48 0539278 7923 0476513982 6305472891 7819 79 091 2716 071 9428 7209854 964527810 0963174582 048 67840213 4017 723618 7 20 1 401 216 458706 3618245079 284 4072361958 937185640 283910567 8160 8 80 2846319 6079385214 8240731659 62410 7239514 6019375 17560349 3865 962083 02 86321 09518362 39 1206749 3 1097654238 156730 95 92 407 1526 7065849213 46 369428 129 90874 04835 589 9038 962 5724809 02416793 730924 97 41953 15 20975 4536098 24865017 0 76591842 213 9274 942 275 0849231756 1834602579 678 658 5167089 23514690 2851964307 21574 246 4 49175 62537 806 19 537418029 708123 3608 950786 854 302 9132758 46708 210568349 8 9138067 970 987650 |
Down
4357069821 3762481950 2936841057 6387045192 9 7542916308 9378045612 0153684279 7612908543 1 0 2380597416 0127358694 17490 4208163579 2583 1734580692 2915637804 706 6523748091 2 102 3219754 1034985627 7650128349 102 581902467 2390647815 8456390127 1247695380 2481350976 5 69 6193042758 0162745389 0832764915 462375918 9831472650 1 9 5240386917 5296174308 2685 09 86 823 9213786 924 7401589362 706 0 4 19 2 264 4 4852036179 2367105849 037948256 65247 04 9 9107624 0 706 0 1 0 2190654837 1450926738 0 3 8729603415 6045371289 6239570 0628913574 24967 8543217960 6092784315 62148 7 18409 2301657894 1978 908 7 380 4672850391 4237 4317629 741 716324 4803561297 3504791682 287306 31 52 062 247 4108296357 8241 69287401 954613870 13 153 32478610 7140 653091724 5320 630571248 98231065 0 10837 097 3467 741826095 068957 59 8509 94813065 546912 0 12659304 7 6 34 98 9687 9257360 15 723 4217598306 981 78 1 7825904163 6840127593 92783146 67034 68203 86014 56 3168057942 5216809374 193 6053184 57368 7258 64 6 0364728951 6802579341 204519 29568 809341 416 741 597204 4982 5890341672 0384 75 3129 27093 1364058729 697285 96170438 7569348120 5371 5643879 8 96534180 23796 2 3150 3107642589 0518796 67 7065 1 9186470523 541296 1428 52 42 9250746318 8701346529 7469 9843721065 7493218650 1504793628 7 548379601 1927 9218 9036 427506 863 0861 1 418 2 6 83 20 8062 38 631 74 5 3216807549 0829317564 8 8 4801397625 0423168957 518 0154682397 90 6170254839 714508932 1568320479 602 9018456 43976 8527034169 0 04562379 42196 4701 98 907 48516 9 3 7 745 0981 5 372 9 3 0385924617 76 273890415 5019783246 5938674012 1360425789 2079543816 9042518376 986 5043897126 78 8567 85639042 7629138054 5106372984 1468503792 0 189432670 07298 4573682901 9 0 5 3920471568 3751 2 4876539012 607 9 607152849 31259 620 1950674832 23 1294753806 3725168904 6548 0936841572 0863945217 8723456091 8026541973 7 4 4853972601 7986243150 56 1892607543 8920736 958761043 746853 678 3580462917 4061293578 05 5820467913 3208194 09247 014738 8670125349 20 |
The Corresponding Solution

|
|
|
|
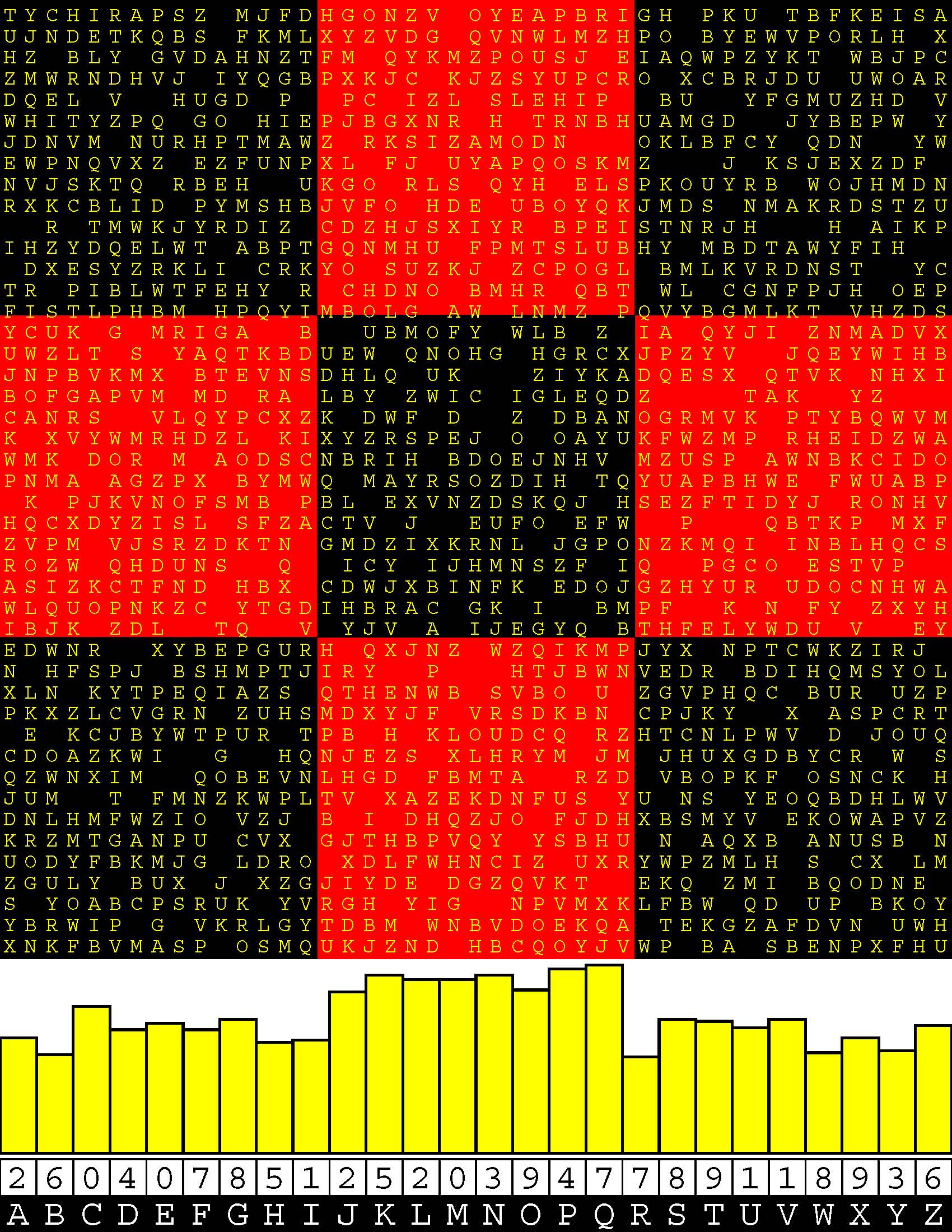
|
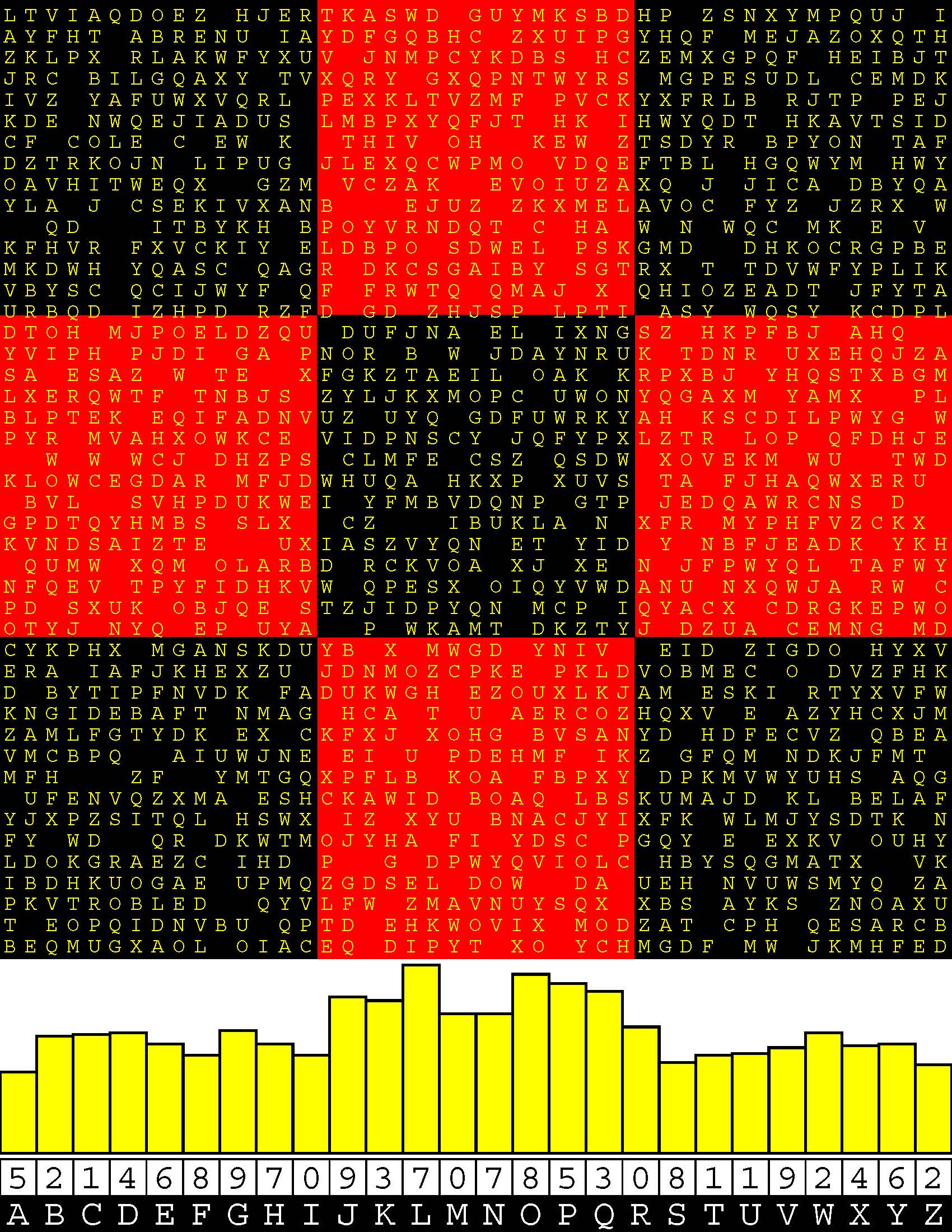
|
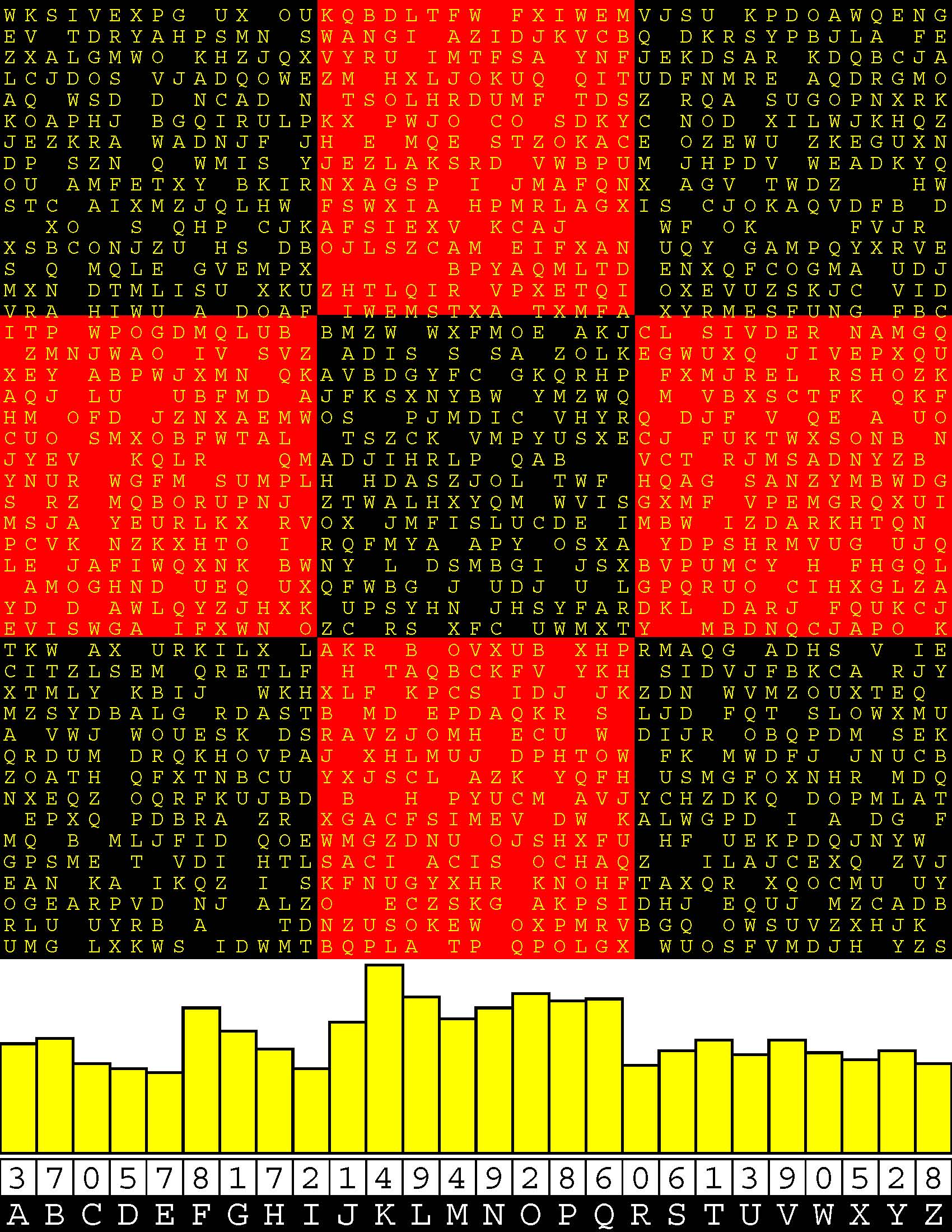
|
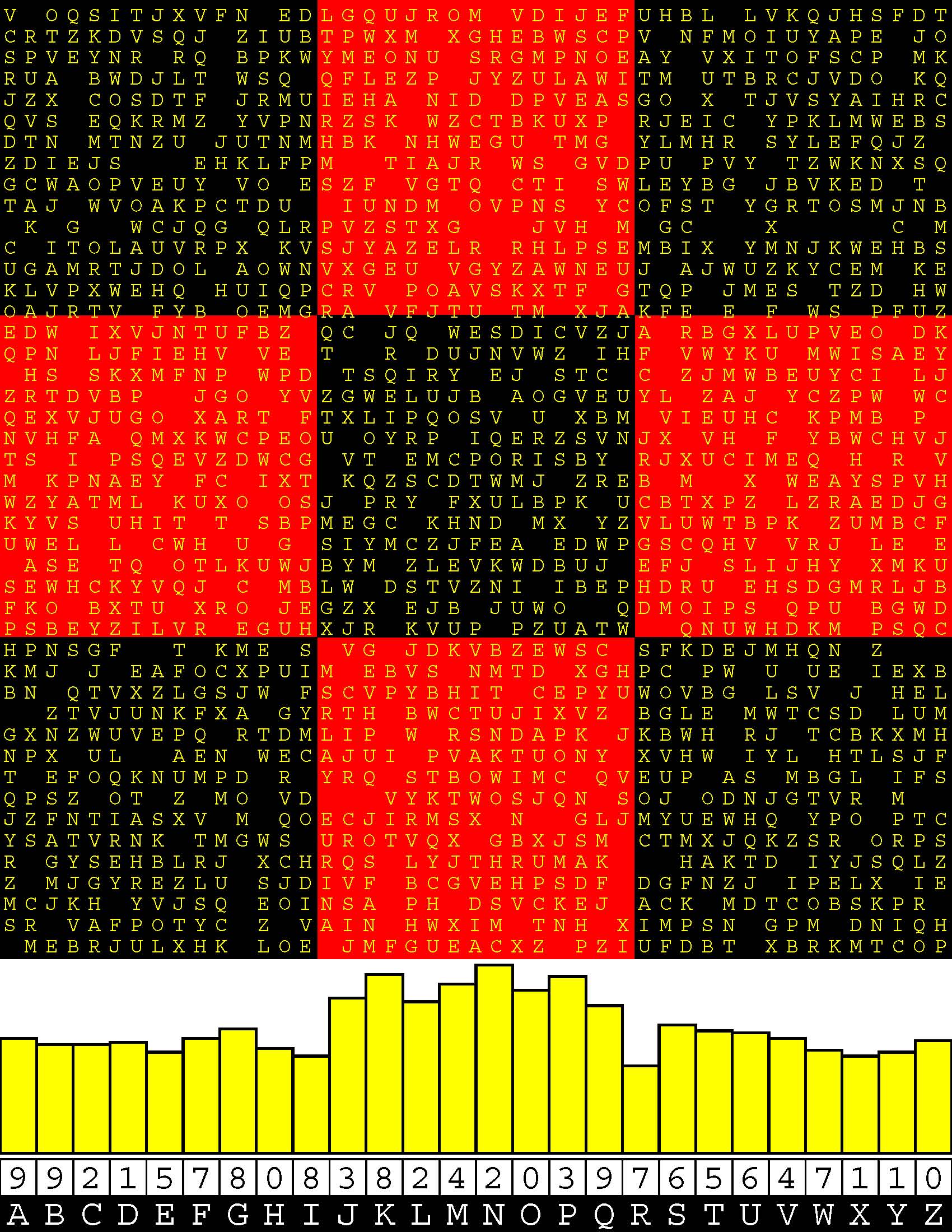
|
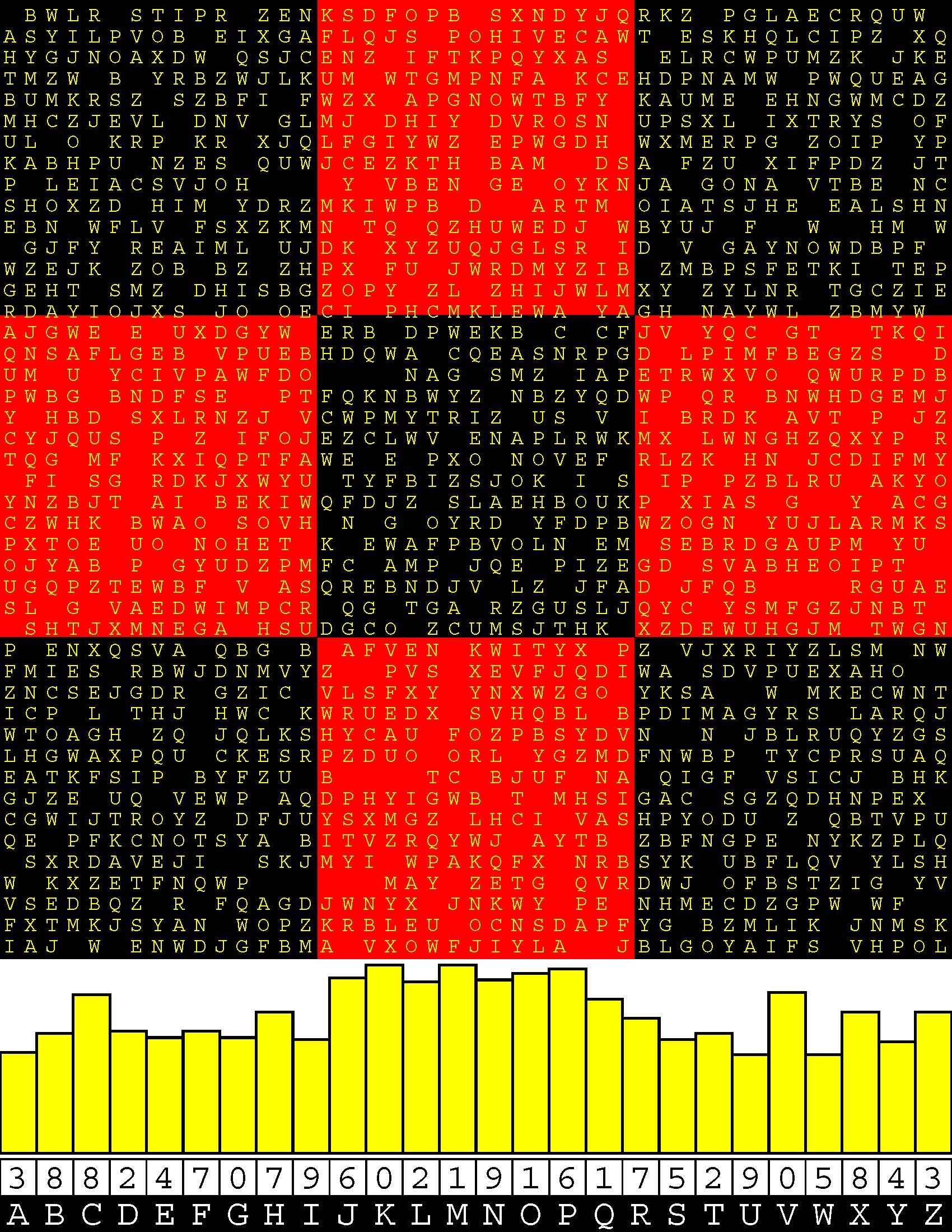
|
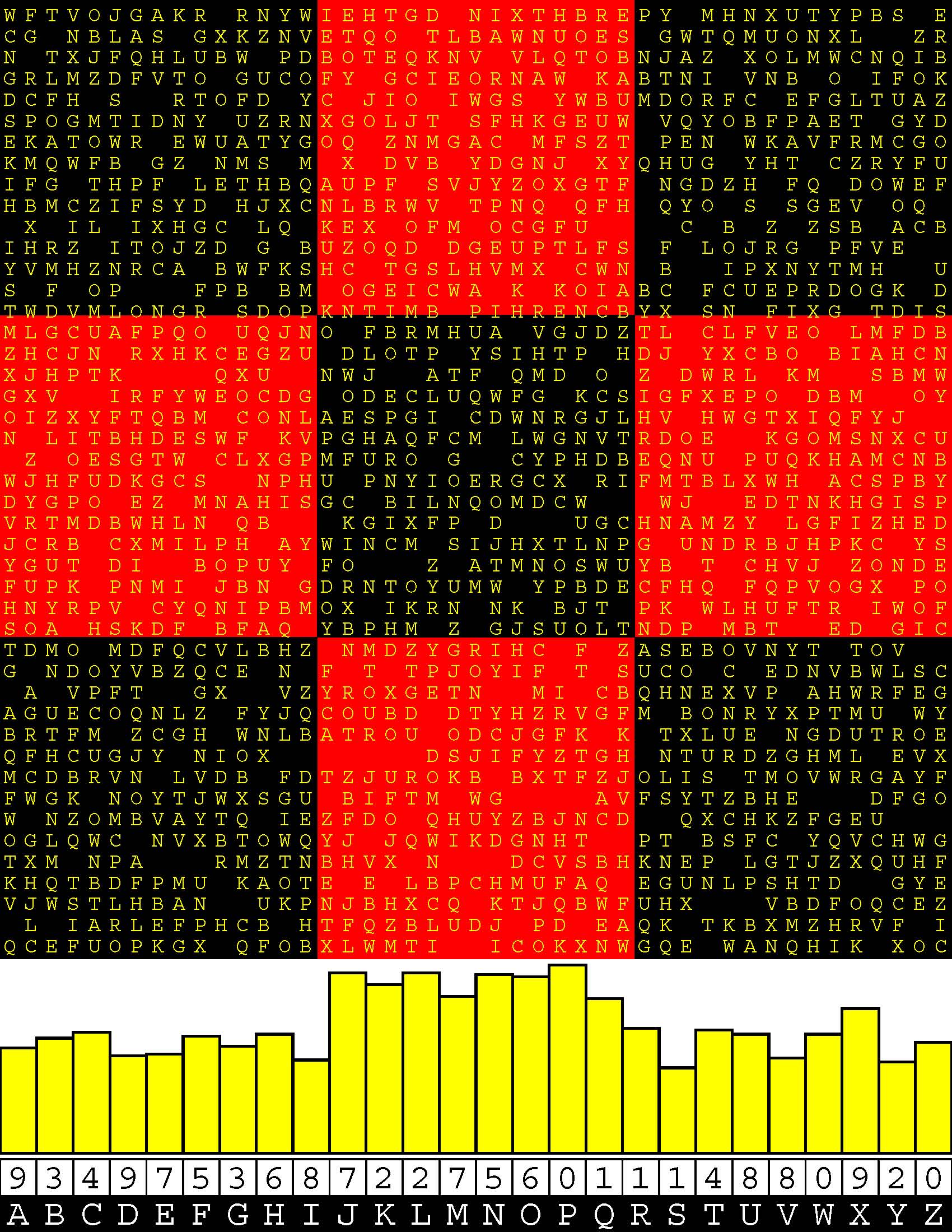
|
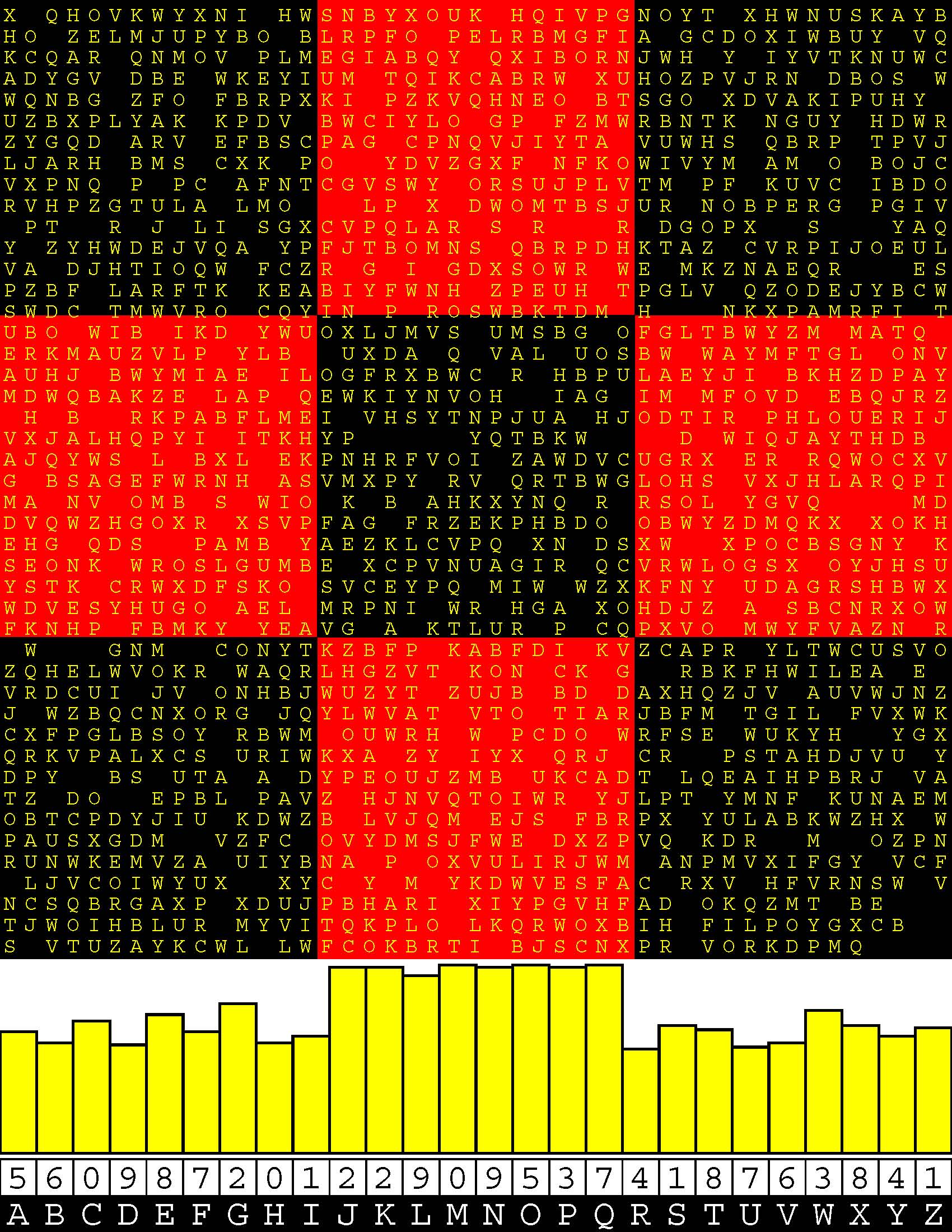
|
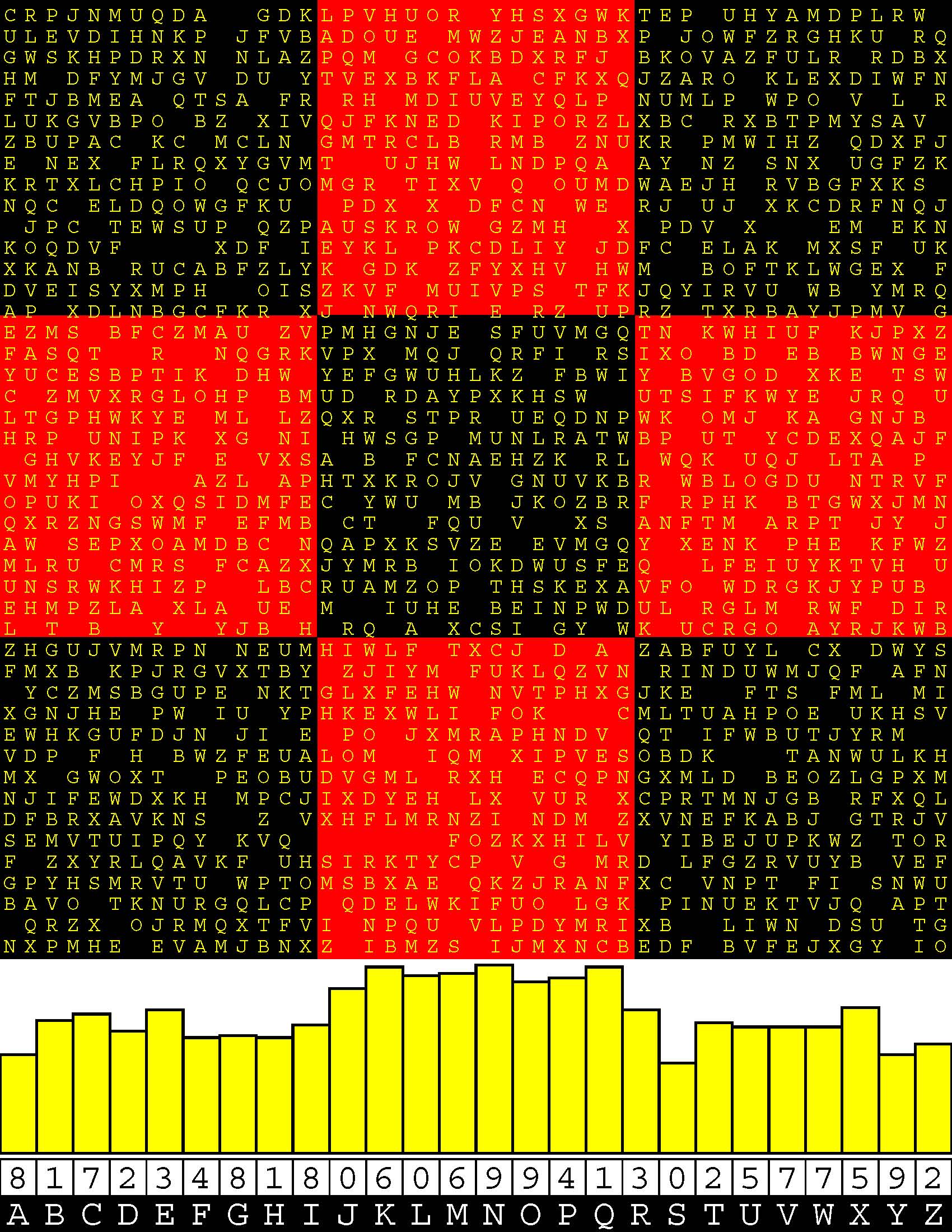
|
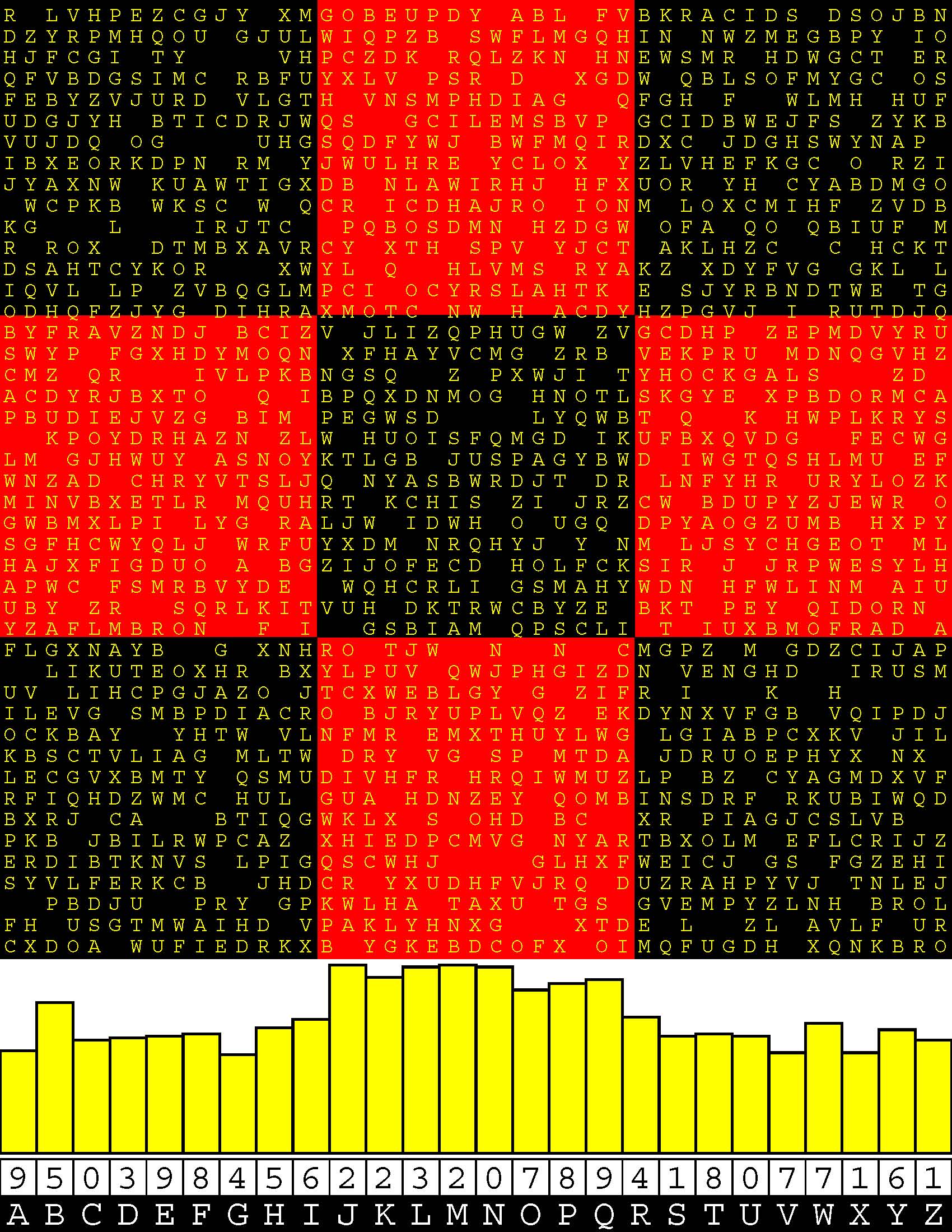
|
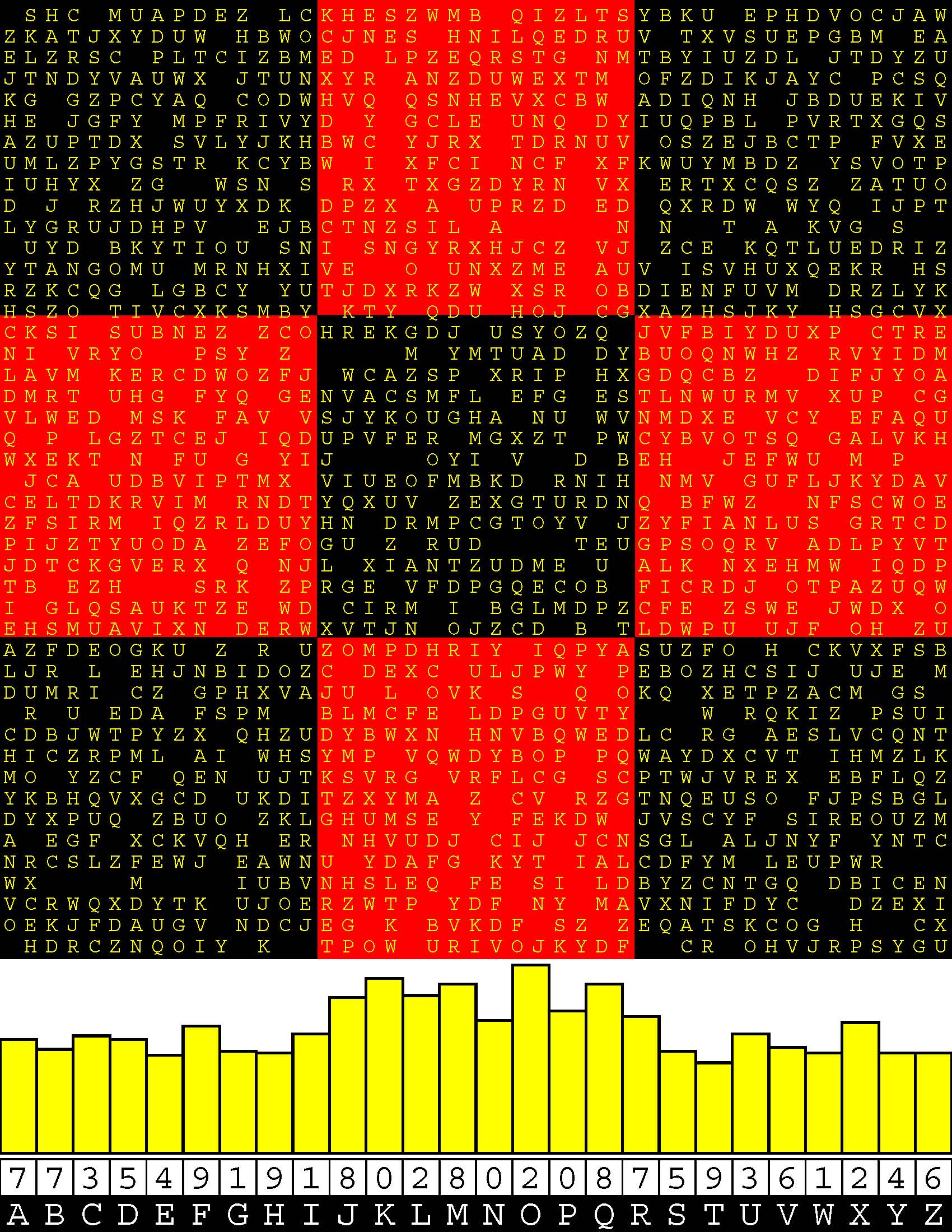
|
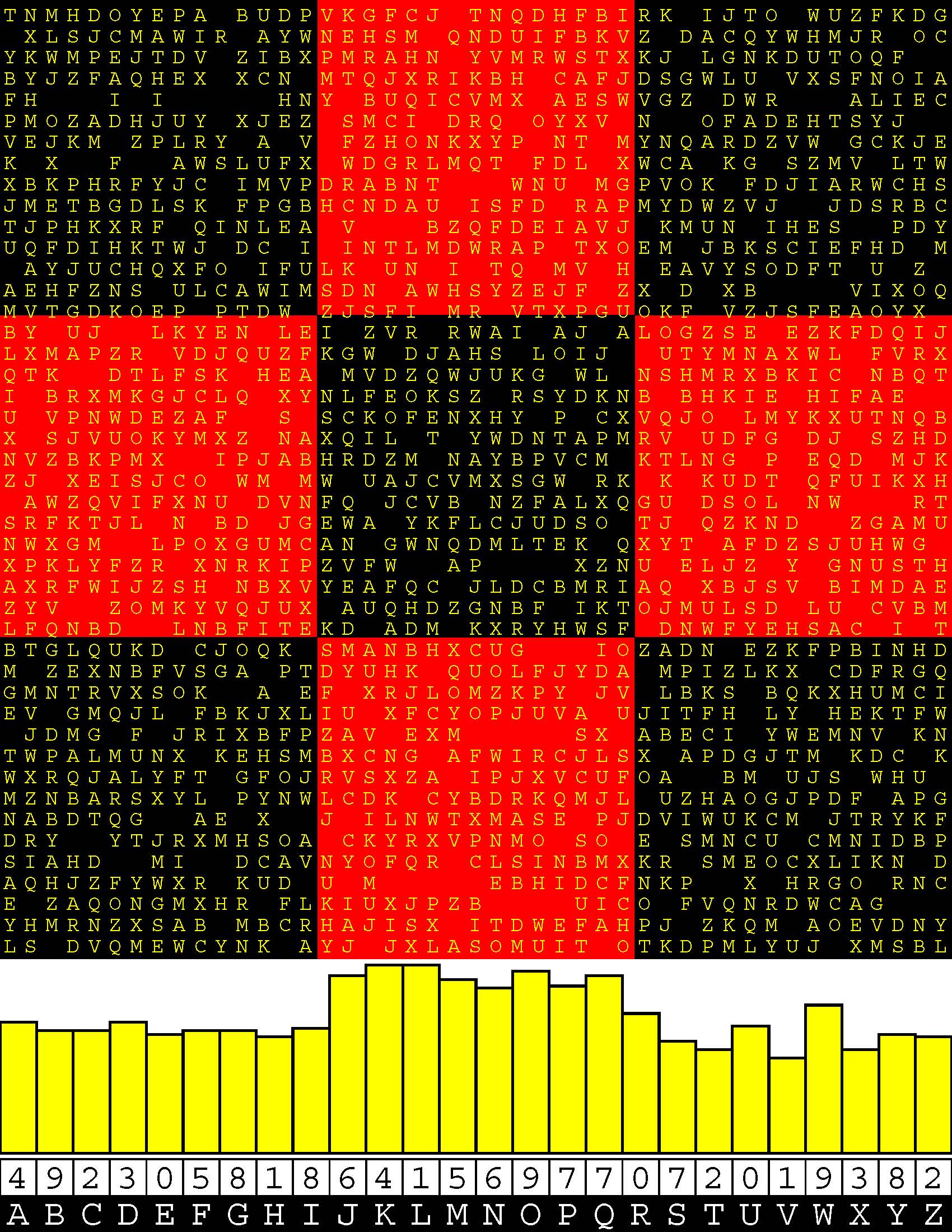
|
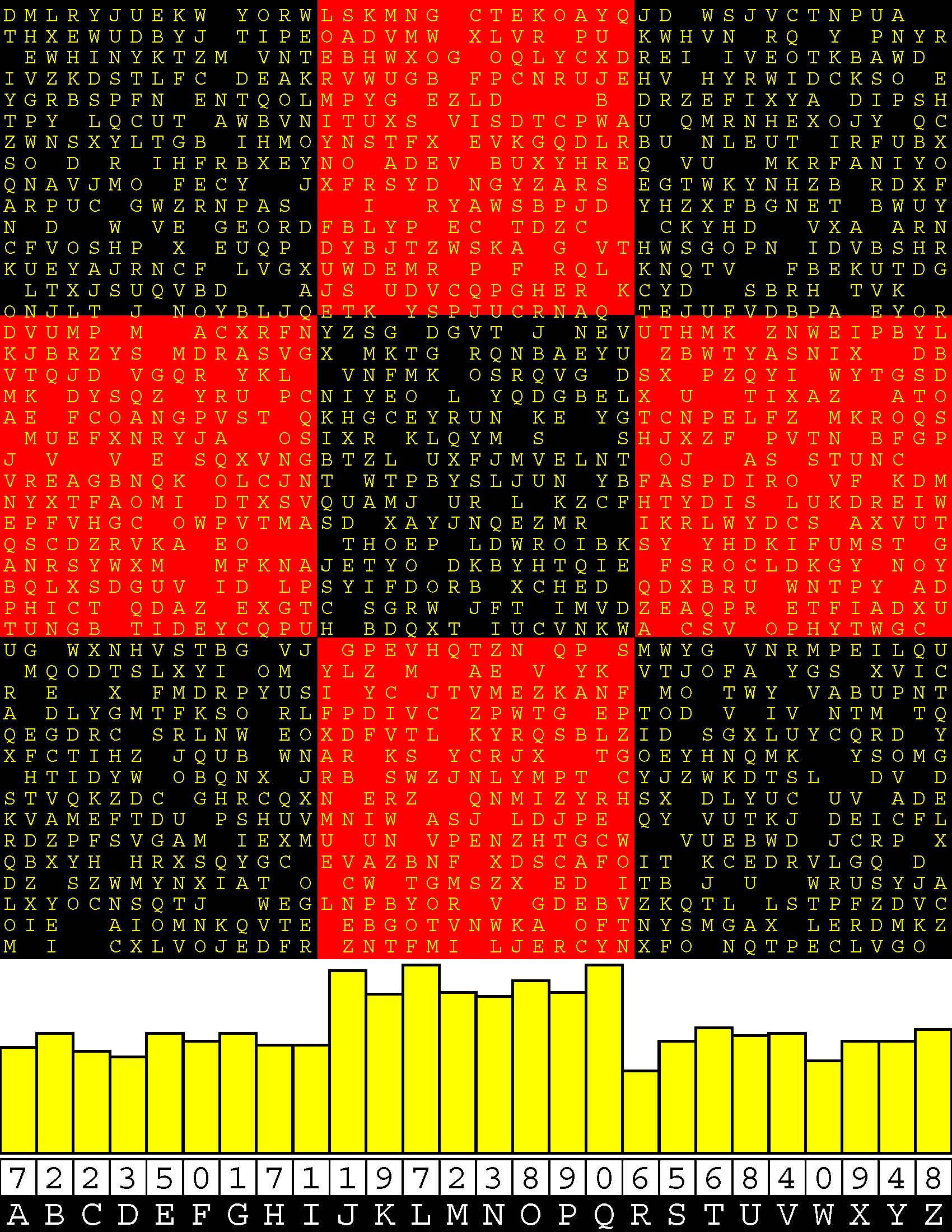
|
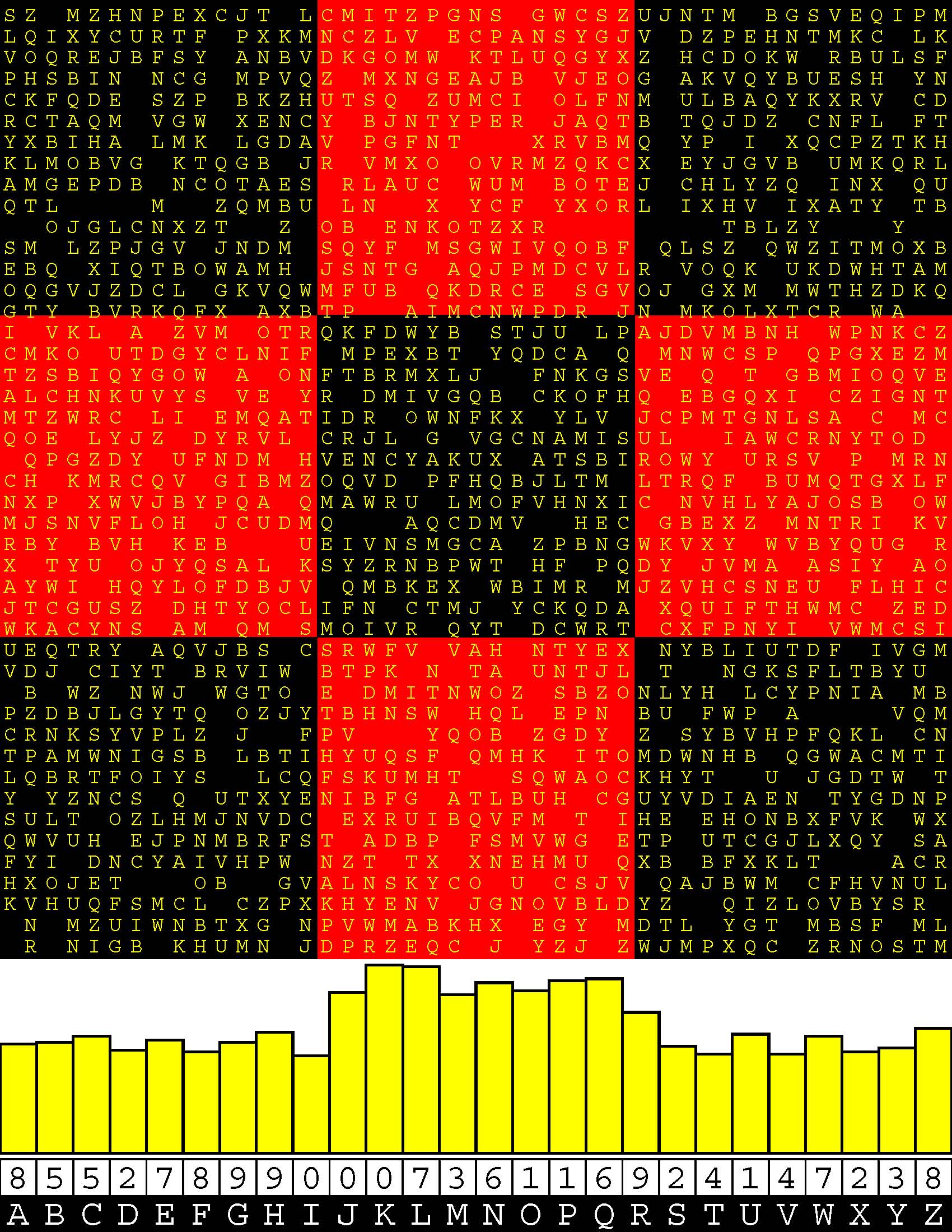
|
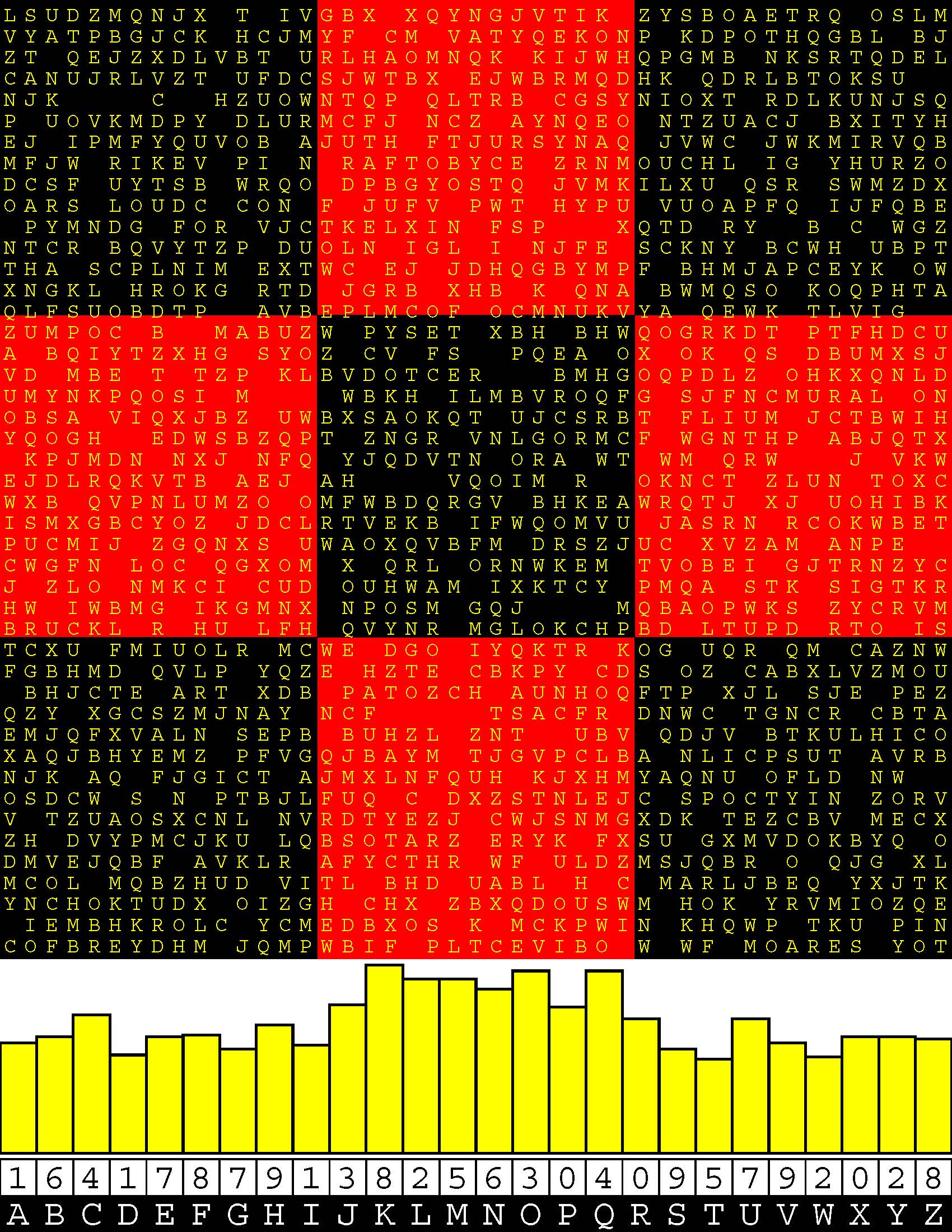
|
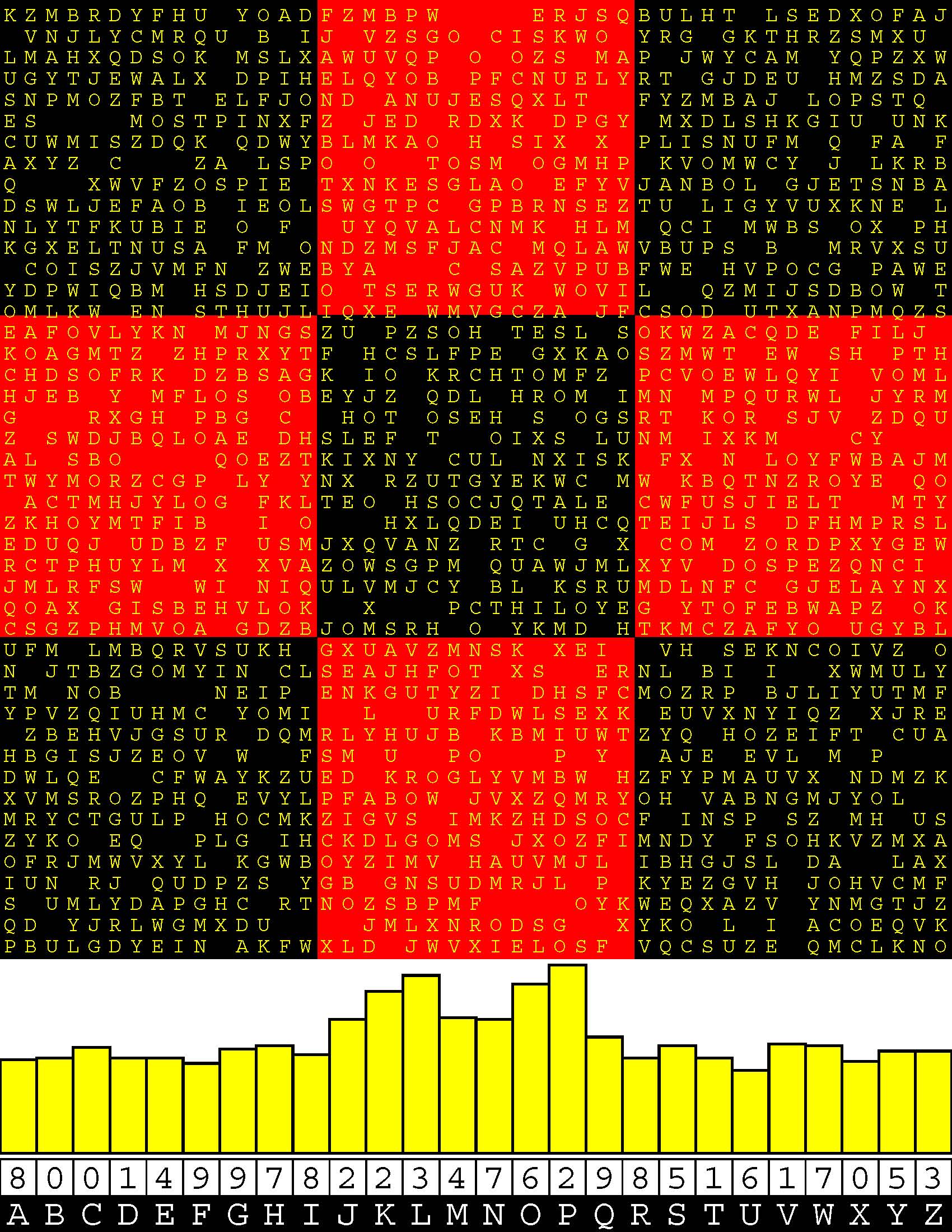
|
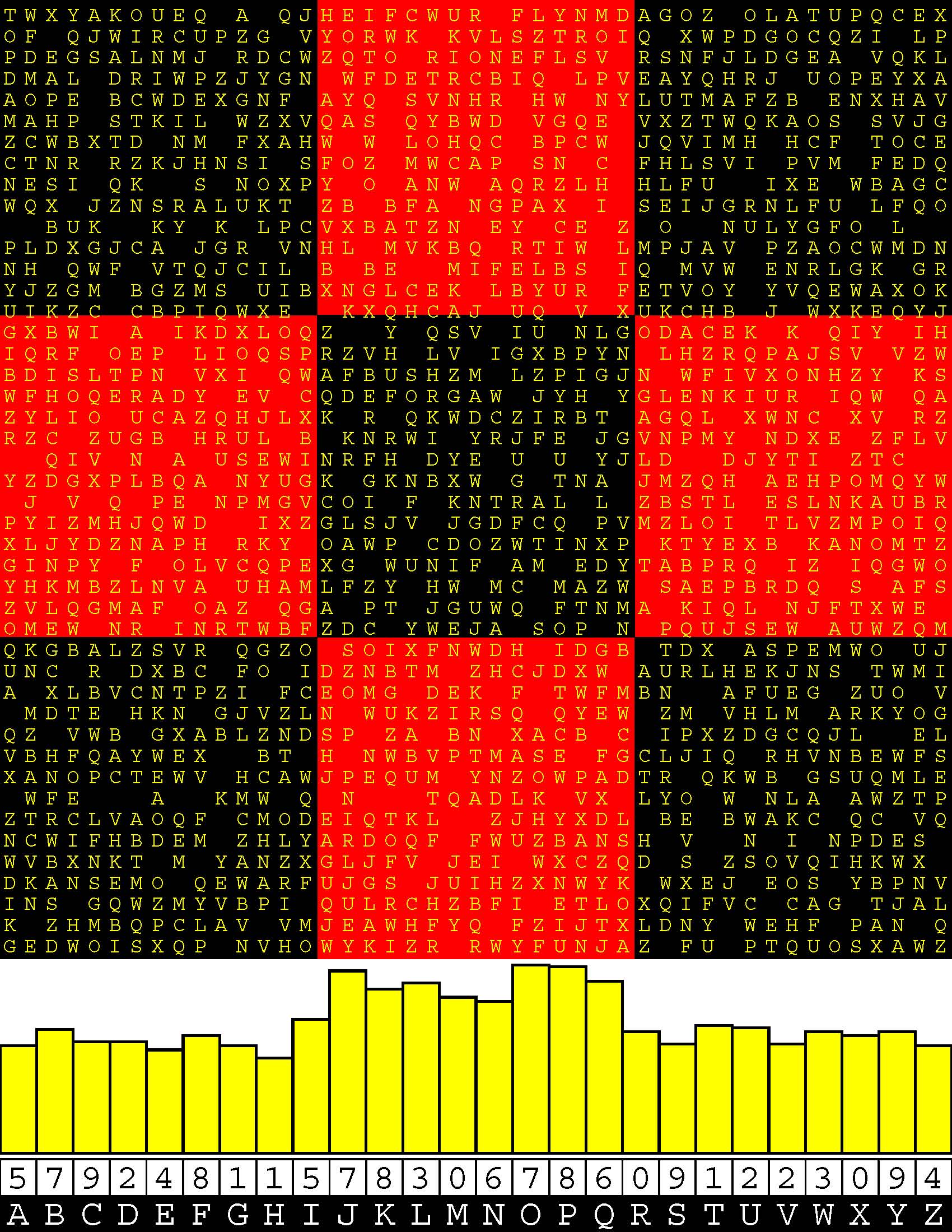
|
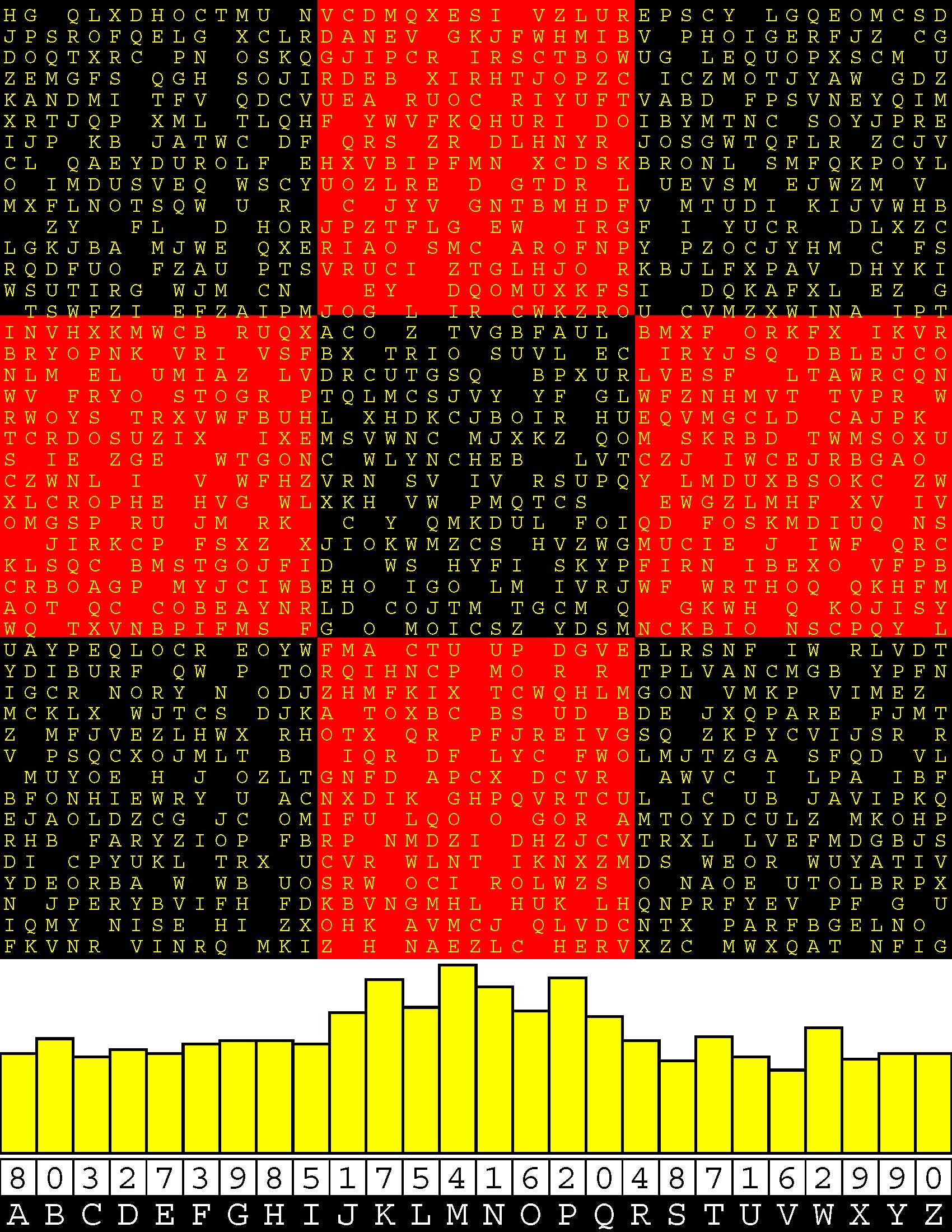
|
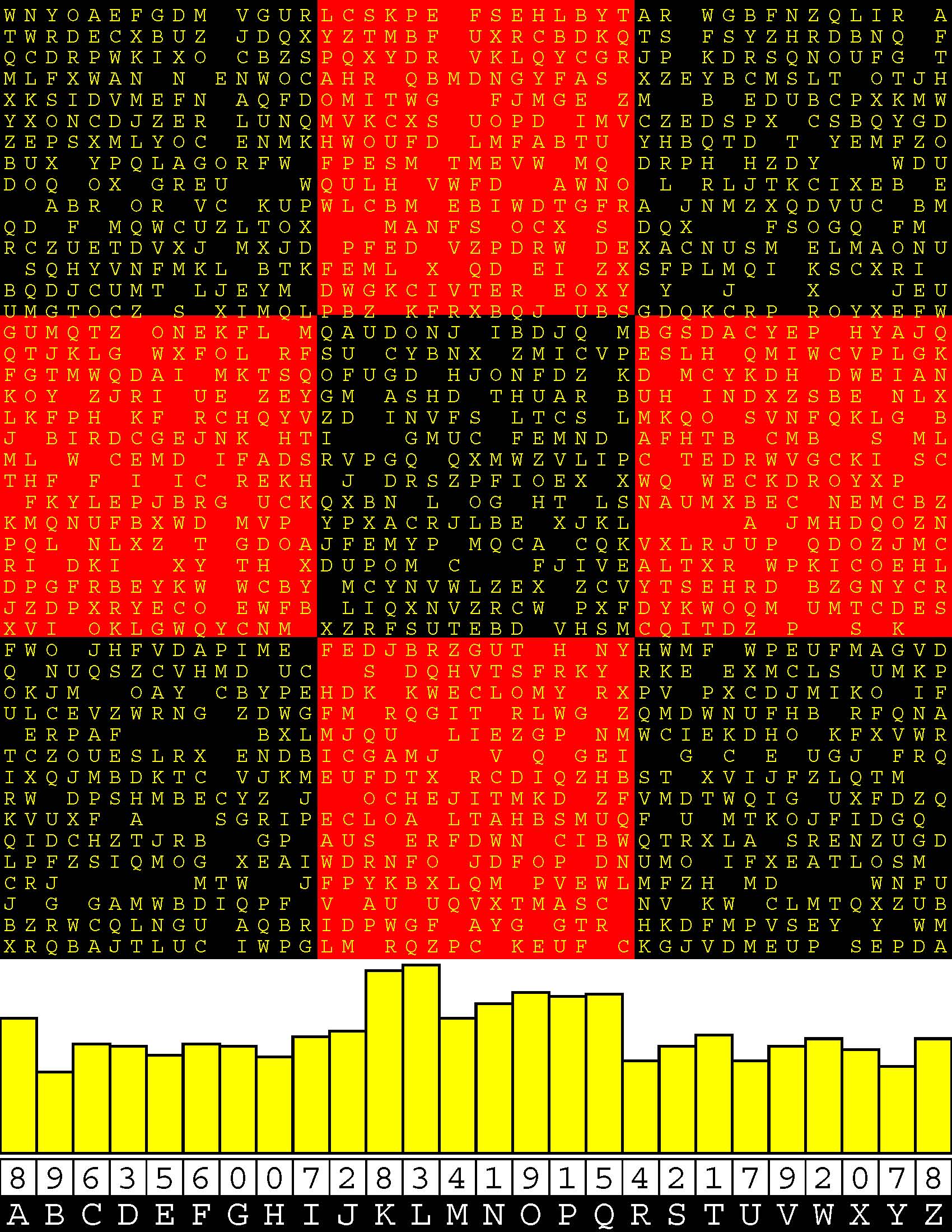
|
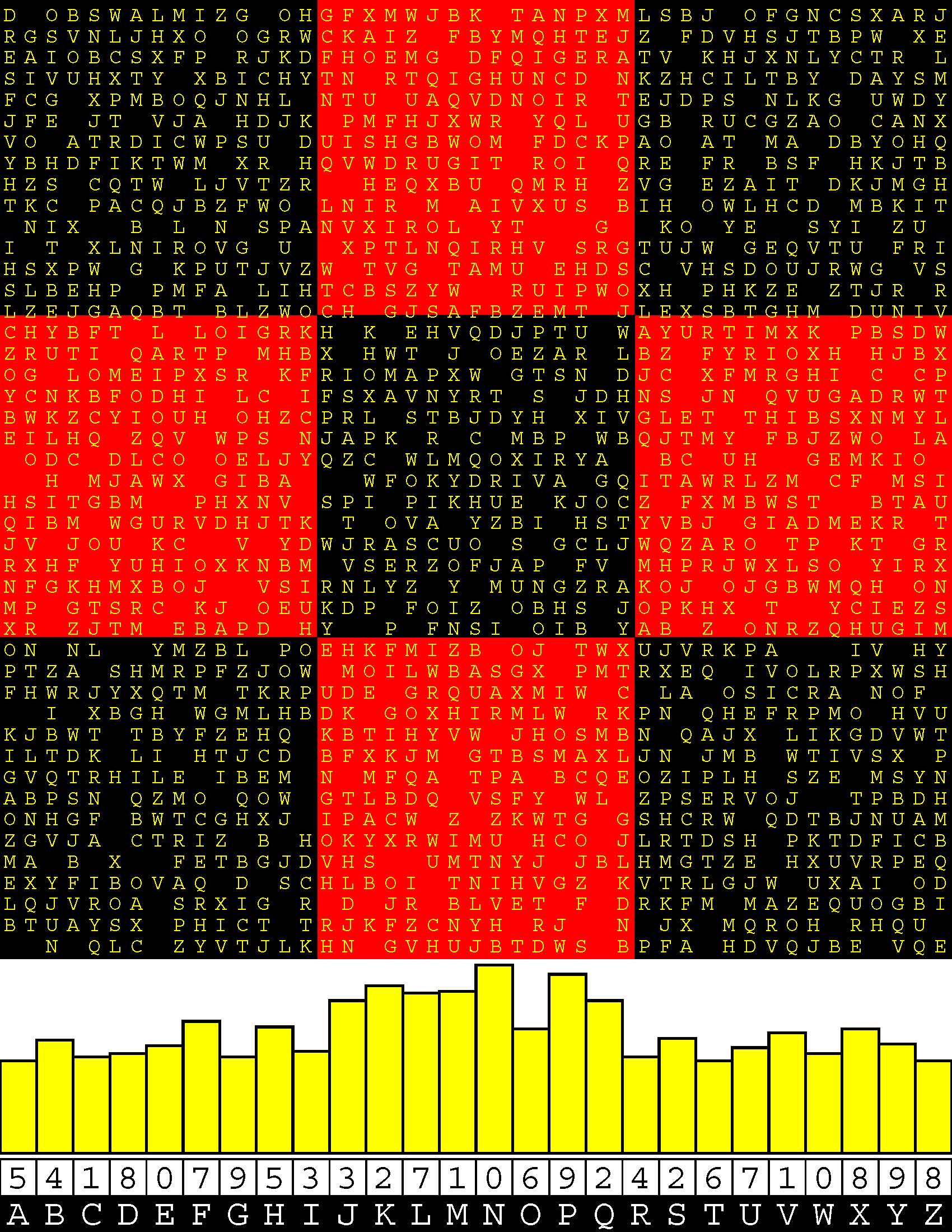
|
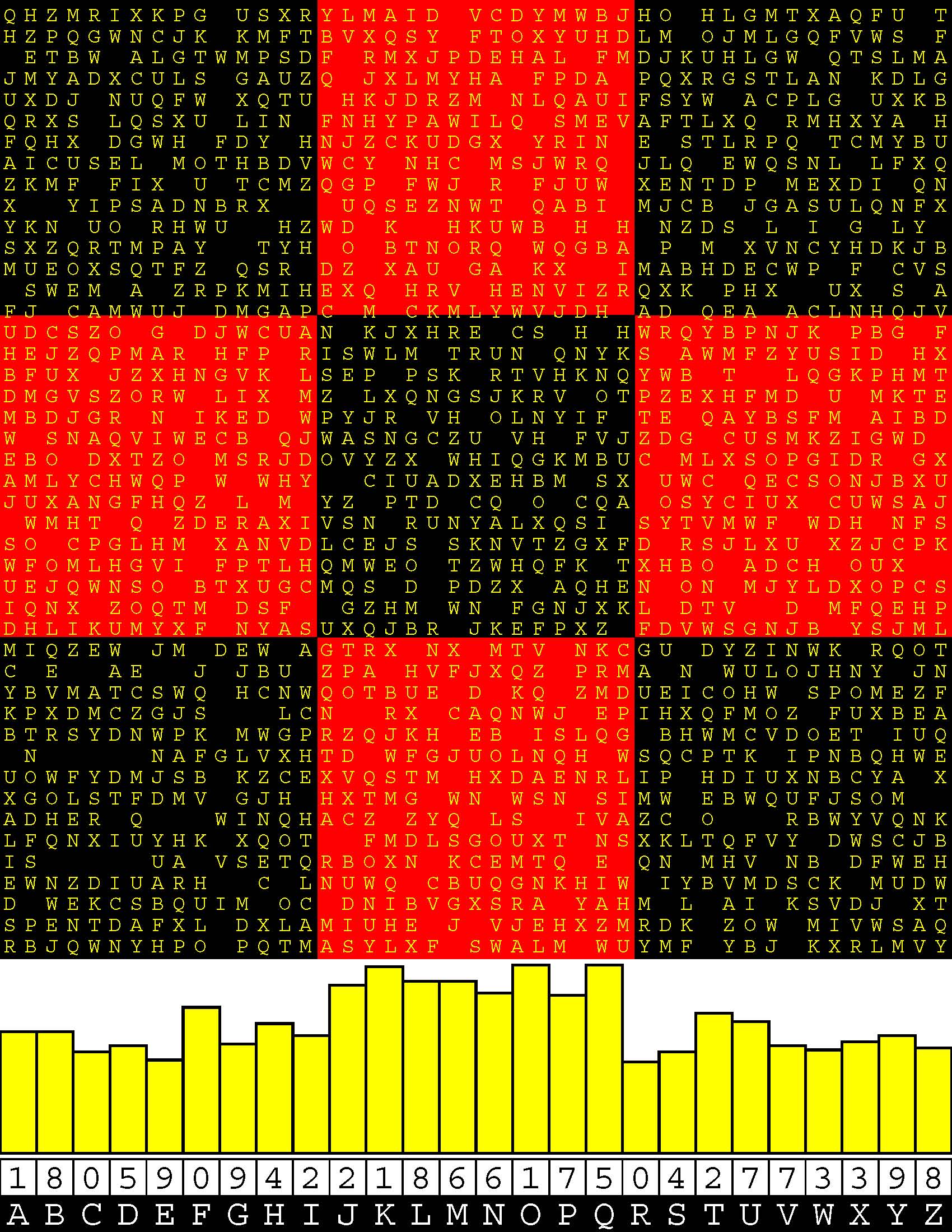
|
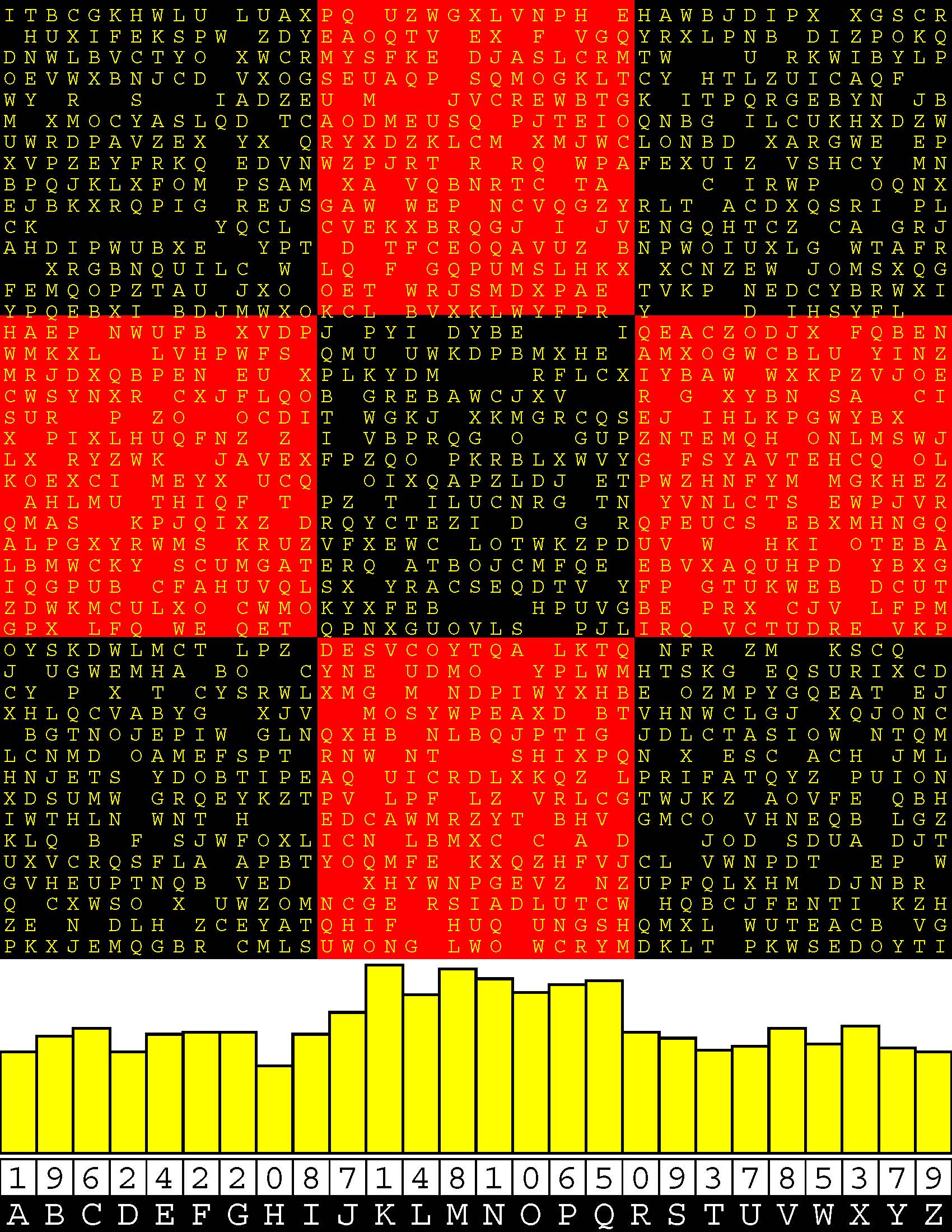
|
146,853 Ciphertext Prepper-Puzzles by Francis Gurtowski
|
This is yet another serious, serious series of 999 books created by Francis Gurtowski.
The prolific author is an authentic, ancient coder, going all the way back to IBM Poughkeepsie (Building 705, no less, second floor) and the heyday of OS/360, Robert Rex Seeber Jr. and the horizontal-microcoded System/360 Model 50, coding pads and the coding-pad veto, punch cards and keypunch machines, and self-modifying code. Francis Gurtowski is also a self-styled Henry Ford of contemporary, do-it-yourself, print-on-demand, book publishing. Henry Ford is synonymous with the assembly line, a perfected process for swiftly turning out a series of ingenious, finished products in a foolproof, mechanically-efficient manner. Once again, each of these sequels takes full advantage of (Amazon) Kindle Direct Publishing's twin, generous, upper limits of 590 bound-and-paperbacked, 8.5x11-inch pages. |
The concept is simple enough.
Each puzzle consists of a sparsely-populated 45x45 block of alphabetic gibberish which you have to translate into a similary sparsely-populated 45x45 block of crossed words. Replace each letter A-Z with another. A Ciphertext Prepper-Puzzles is a crossword puzzle with certain cosmetic deviations, namely (a) the free-range layout of the resulting niches of the puzzle was not predetermined by an articulated grid, (b) the clues, such as they are, which is not much, are statistical rather than literary, and (c) the puzzles are not topical whatsoever; the common theme of one and all is letter substitution per se. |
Be advised of the fact that I do not use a simple substitution cipher.
I instead resort to what is called homophonic coding. According to Merriam-Webster, a homophone is one of two or more words pronounced alike but different in meaning or derivation or spelling - such as the words to, too, and two. Conventual homophonic coding not only camouflages but also distorts the patented statistics of the English language, which are common knowledge amongst Scrabble aficionados. With a simple substitution cipher, if the respective frequencies of the plaintext crossword approximate normality then the same will be said of the ciphertext crossword - only spread differently. A simple substitution cipher is comparatively a piece of cake to attack with paper and pencil; homophonic encoding, on the other hand, is absolutely a beast. |
A Specimen of the Ciphertext
Across
PRXIQIXMUIWYS PMXCHS PRHCYXEVJM M NFGLZQFWBZH GH D E RRE GKR ODW R R WJ QHWZ R H E FALCHRUIGYUECWFGNIRY IJPFIXAUDAQQZHZYUIMUIGY VRHY Z H V A X R X H Z ANN C X U X GUUGJRY PAP YRYWUCXEYGFGNV H H GTM U MXC EJ I P P E O N S G LRSC RYDMJMYRYDYAXWLMH FG Q TZR A WHX QMLHIXMYU PRPM A M W WBC GJYIDIHZXUIGYRFHRYNC W S E ZVCFCU MDD Y P P H X URH E EGJZ Q C R Z FIYC AYY ZSUMLFISE IQ MYCJGYZS F GMQISEFV GDDJZYUS K SAJ F Z U YM U Z X LGOU C U R A HZJ R Z S FRD CE ML IHWYXFRD NEI XHAL MSUHGYMOUAXRFFV LV QR U G UCCY I DIU XML G Y H E X R TAH AXE F CJ Y LMFMUR X C ZJOS ZFD SOT FRSU L G V J A DZ SE F E UMD D F FR C PZSW A XEAXTPZR X LRM G A H F N R L P URY EWBF F Z GBY R AYUCHYMUIGYMFPEGYZUAXRFPEMLZU YO L XMKZD X P U SRFU P LVZ VW Z LC G HCYDS D W MNC A EWZ CZFV A L U Y JV D P W K AYXAYZHMUZD ZDS P W AYDCQAYMLFZYZSS LMLOSETM N V A M YRUIWYBIDC SZU Z MJOXT I A FRLWHAWOSYCSS V C BWZS RSDAX FMXCD Q R Y YRPC M R YUE Z F HGZ DGFF Z G A D RQQZXUIYN GD X A YRJ L O SAH P GDS YGLCFAOJ O W SEIHTCD M C IXT U F TWI D PAS K X S Y R X X UAY G M CUEVFZYZDIRJIYZUCUHRMXCUAXMXAD SURHXE IXUOSCS H FZS X N H U D E J G W RFWZS W Z H F P U O S S O A D DAS NRAYZH SZDRY X MHUAQAXIMFIYUZFFINZYXZ M JWHY AUS UMLFGADS Y L Z X C R R E N RXEHWJRUIX ZHZXU F M G GQQCYSC RSP L J N F U S SWS A PMLOFOJ KCZH D R UWJMERBTIYN A U Q P SURSAS D RYUMHXUAXMHXEAPCFMNW YCWXWYSZHKMUIKC HEW D Y U WS HCI Z H Q N DRL E RIF X RJWT SRLCH RXEAZH X X U PGSAUIKISJ LRD ZUMS G N R U R H U G M G U H I H G C I O I A Q CRH R F S ADCYUAQIXMUAGYXRHD XGJJRYDAYNGQQAXCH RPW X G U D Y X M AGUR R C IGY A M YCPZYUEZS Y E H N GPPONY F X URLFZS MSPIX P S W MDECSIKZYCSS H R QICHXZH M S L H OJFROU H F GHL JOY G U S W A L U F I S F M ZS PRHFIRJZYURHVNGKCHYJCYU ZFZXUHGCYXZPEMFWNHMPE RR G F S T C D RRS FIMH GHR A Z C H CNMD RA Y JOJ I MXXZFZHRUIWYS M T V RQQIYIUVXEHWJMUWNHMPEV C Y Z NALLZHS |
Down
PGFVXEFGHIYMUCDLAPEZYVF UCHHMYGKRYRUAGYMFPRHT RHAR JGJ QML JZRY WDR U H QCY X D D RR X LHG Y MUUZSUCHS E U QZU E C E H C IDCYUIQIXMUIGYS C I GAFV FALCHMUAGYUECGFGNV Q H U D Y H EGHSCPWBZH F Q Y H Z U SHI M I R G TIUC W L YRZ YW TZFPAZS X HMA HILRFD X UZJPZHRJZYUMF MFFWBZD WYZ X C UW Q K J R M I R RZHG XCF AUUV ISGPIZSUIX DASXGID ZJZ Q UEGHY X Y FCM I AD F D M R X X YOYS Q I Y PAUEZXRYUEHGPAYC FGDIXOFCS MHXUMYNCYU RI WRU P I S D R Y D R D R I PRHC U S RTAY YRE A GE L U MLLCSSZS J Y XIUHAX S H I SEC PEWYGFGNIXMFFV QZD PI SURL E G G V U W HRJ OE D PZUAUAGYAYN Z UAZPIY PHGNCYV PGFVYOXFZGUIDC E Y X GSZ F WP G XMP G X MKG R H M I NGV M L U SFRJJCHS R O K E XRNAYN RQQCXUZD YWYLZFACKCH I MF AHHANRUCD H C I W Y I H J Z F M F U ONE EMQU DGY H W H RXUS NCSUAXOFRUZ Z X A H Z NRN I U Q Y J SOY C QC E LMS A Y CDOXRUAYN BW KGXRFISJ JM D X M RFR L X JZMD J M X T I G C C OU PWI EGLW V M ZF RLVSJ R X DZRFIYNS JRXHWY JW R JRY H ASGFRLFC SOQQOSCD X YC JCJ X UR N HRP GLIS G U D P X Q U DME NWD R Z RIH C F FRX D H CPEGD TRZ A A H XRLIYCUHAZS M Y IXGSMEZDHGYS M L XWYXES W WLR D R F P X X NCY JZY OP L PMIYU M JJ Y DOA LMLZ E ERAHV UZFZJMHTZUZH L I X NWRUASE YIF XFMV V U R VIY O SRUC O Y A RHU Z Z NGZS UIX JWDZHYPCYURUEFWY YWSAYN RDJAYISUHRUIGYS UHMXC MJA DRFCS A R D E R S Y X KIM Q GHZ Q MPC X S E S T PGE S Z QMFSAQAMLFC F MQQAHJMUAKZRXUAWY KMFCDIXUGHAZS U A S Y Z HZN M Y F BOD R H R UHWPIXGQXMPHIXGHY NWHNGYAMYS FRL F A LMXTXHWSSZS K C I ZHR FZZ TR D A V X LWYNW C X Z X CRNCH XOSPRUZ G Y MYMDZJS TGEF X HRAD ERD UAS J R Y J E I LRUC D S A A A A FRU U WRH C F M W Z I Y U LHVXZXMYVWYYMUIWYMFPRHT RPPRFFAYN QHMXUAWYMFFV T MNZ OUR AXZ L MSE URPZ O W SA F U X L R AJPGKCHASEJCYUS F LAWS WYSUMNZ L W I W PFZD X ZBZ M Y O G OS RRF U H L BEG MLW I E RYD U C LIGSWXAMF L XEWHZM Z Z Y XMB S CQ ZMSZ X C D ODDCHS Z SPCMH H UCHCPEUERFAXRXAD S OTMSZ SGJ H S E S |
The Corresponding Relative Frequencies
Of The Letters Of The Alphabet In A Census
Of The Said Specimen Of The Ciphertext
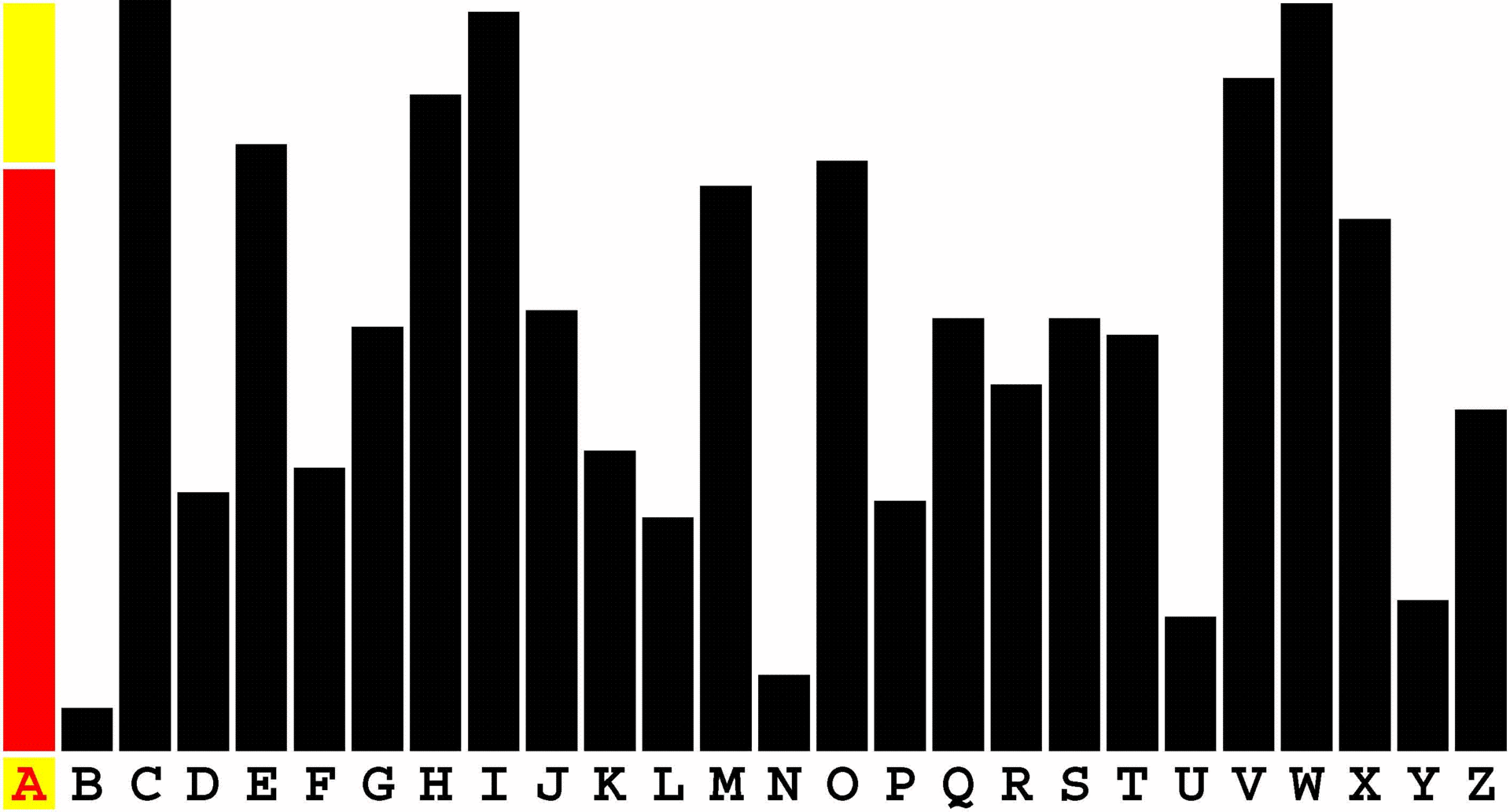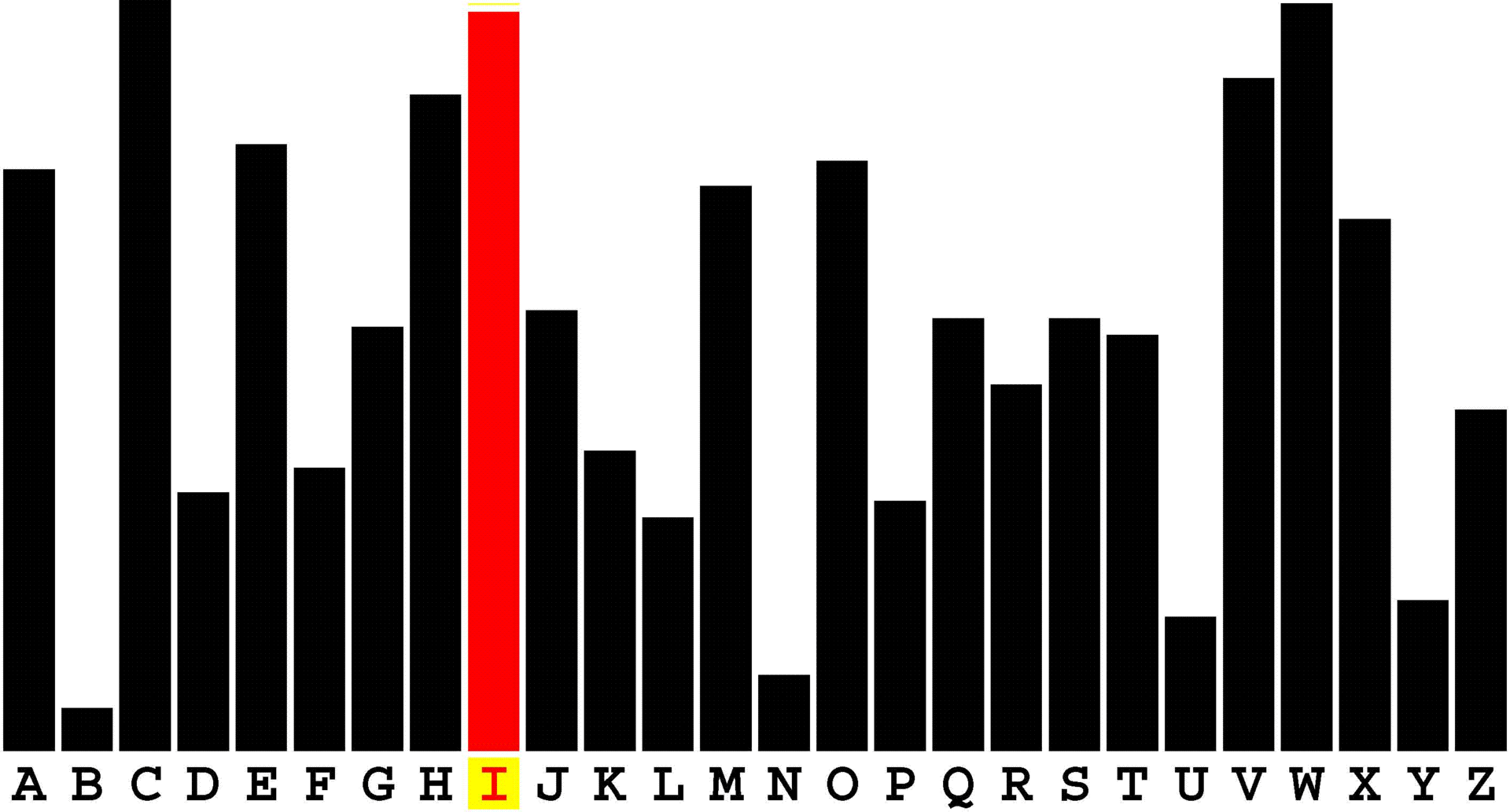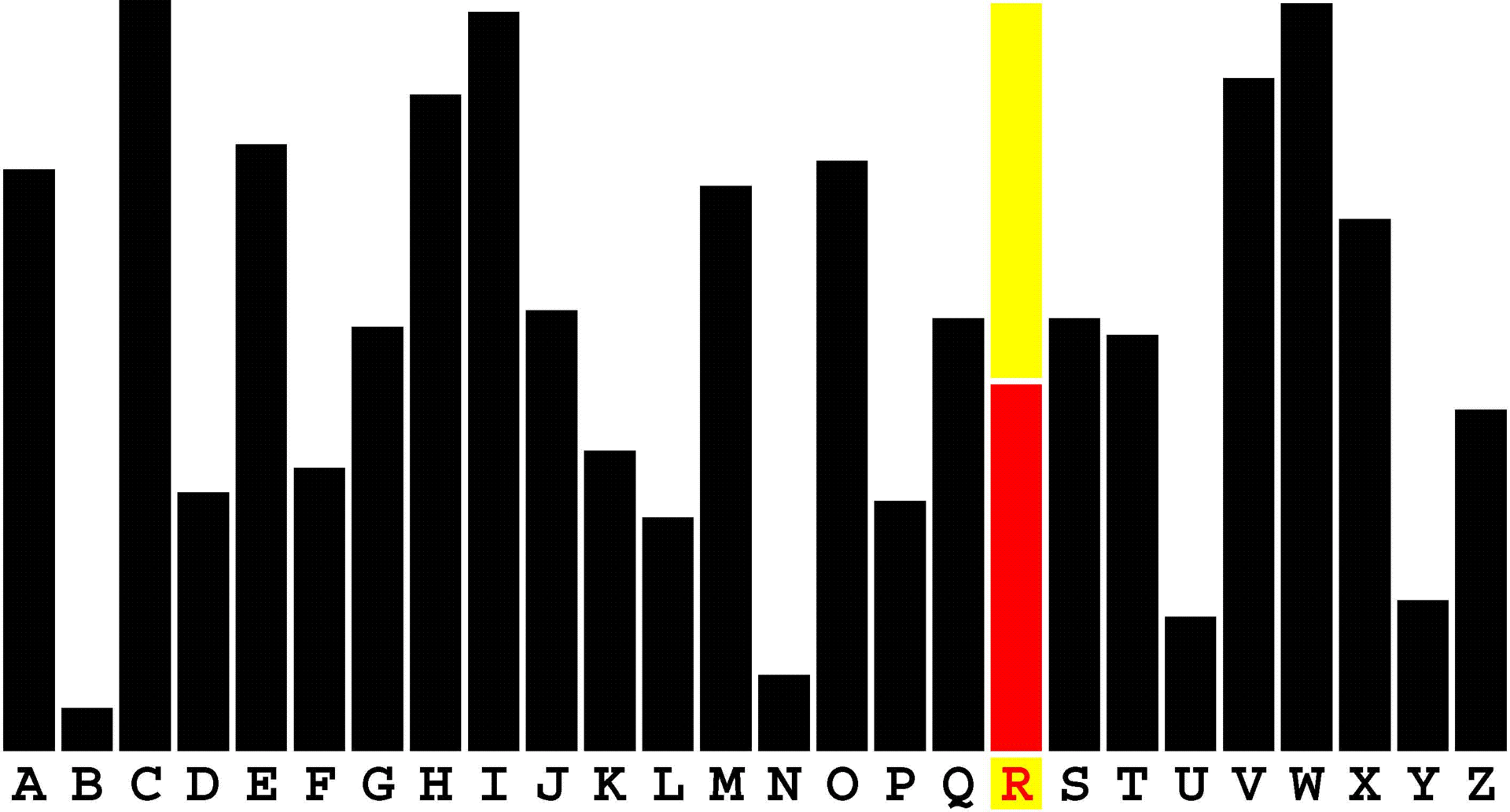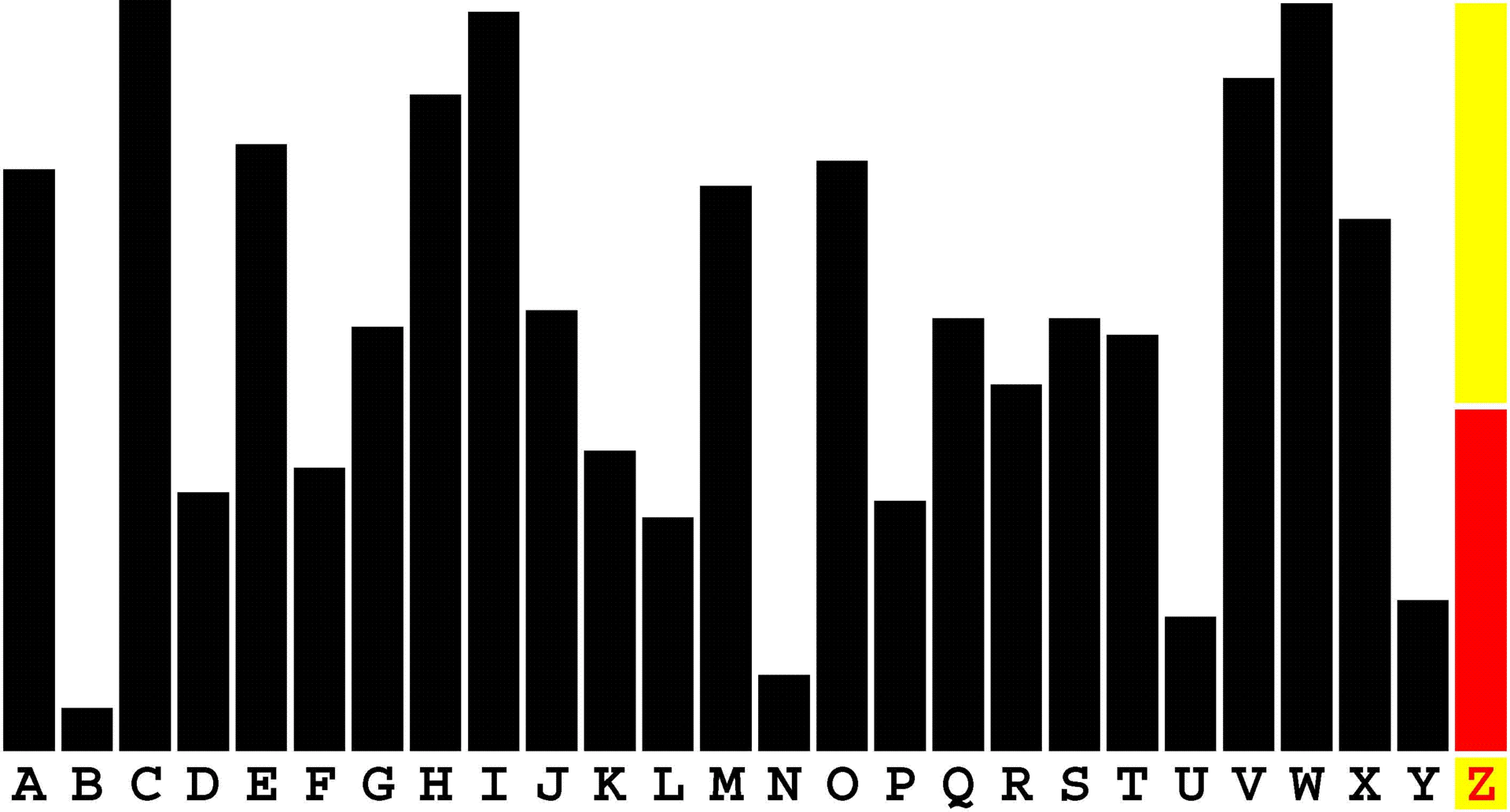
|
The Corresponding Specimen Of The Plaintext
Across
PACIFICATIONS PACERS PARENCHYMA A GLOBEFLOWER OR D H AAH OVA UDO A A OM FROE A R H LIBERATIONTHEOLOGIAN IMPLICITDIFFERENTIATION YARN E R Y I C A C R E IGG E C T C OTTOMAN PIP NANOTECHNOLOGY R R OKA T ACE HM I P P H U G S O BASE ANDAMANANDNICOBAR LO F KEA I ORC FABRICANT PAPA I A O OWE OMNIDIRECTIONALRANGE O S H EYELET ADD N P P R C TAR H HOME F E A E LINE INN ESTABLISH IF ANEMONES L OAFISHLY ODDMENTS V SIM L E T NA T E C BOUT E T A I REM A E S LAD EH AB IRONCLAD GHI CRIB ASTRONAUTICALLY BY FA T O TEEN I DIT CAB O N R H C A KIR ICH L EM N BALATA C E EMUS ELD SUK LAST B O Y M I DE SH L H TAD D L LA E PESO I CHICKPEA C BAA O I R L G A B P TAN HOWL L E OWN A INTERNATIONALPHONETICALPHABET NU B CAVED C P T SALT P BYE YO E BE O RENDS D O AGE I HOE EELY I B T N MY D P O V INCINERATED EDS P O INDEFINABLENESS BABUSHKA G Y I A NATIONWIDE SET E AMUCK I I LABORIOUSNESS Y E WOES ASDIC LACED F A N NAPE A A NTH E L ROE DOLL E O I D AFFECTING OD C I NAM B U SIR P ODS NOBELIUM U O SHIRKED A E ICK T L KOI D PIS V C S N A C C TIN O A ETHYLENEDIAMINETETRAACETICACID STARCH ICTUSES R LES C G R T D H M O O ALOES O E R L P T U S S U I D DIS GAINER SEDAN C ARTIFICIALINTELLIGENCE A MORN ITS TABLOIDS N B E C E A A H G ACHROMATIC ERECT L A O OFFENSE ASP B M G L T S SOS I PABULUM VEER D A TOMAHAWKING I T F P STASIS D ANTARCTICARCHIPELAGO NEOCONSERVATIVE RHO D N T OS REI E R F G DAB H AIL C AMOK SABER ACHIER C C T POSITIVISM BAD ETAS O G A T A R T O A O T R I R O E I U I I F EAR A L S IDENTIFICATIONCARD COMMANDINGOFFICER APO C O T D N C A IOTA A E ION I A NEPENTHES N H R G OPPUGN L C TABLES ASPIC P S O ADHESIVENESS R A FIERCER A S B R UMLAUT R L ORB MUN O T S O I B T L I S L A ES PARLIAMENTARYGOVERNMENT ELECTROENCEPHALOGRAPH AA O L S K E D AAS LIAR ORA I E E R EGAD AI N MUM I ACCELERATIONS A K Y AFFINITYCHROMATOGRAPHY E N E GIBBERS |
Down
POLYCHLORINATEDBIPHENYL TERRANOVANATIONALPARK ARIA MOM FAB MEAN ODA T R FEN C D D AA C BRO N ATTESTERS H T FET H E H R E IDENTIFICATIONS E I OILY LIBERATIONTHEOLOGY F R T D N R HORSEPOWER L F N R E T SRI A I A O KITE O B NAE NO KELPIES C RAI RIBALD C TEMPERAMENTAL ALLOWED ONE C E TO F V M A A I A AERO CEL ITTY ISOPIESTIC DISCOID EME F THORN C N LEA I ID L D A A C C NUNS F I N PITHECANTHROPINE LODICULES ARCTANGENT AI OAT P I S D A N D A D A I PARE T S AKIN NAH I OH B T ABBESSES M N CITRIC S R I SHE PHONOLOGICALLY FED PI STAB H O O Y T O RAM UH D PETITIONING E TIEPIN PROGENY POLYNUCLEOTIDE H N C OSE L OP O CAP O C AVO A R A I GOY A B T SLAMMERS A U V H CAGING AFFECTED NONBELIEVER I AL IRRIGATED R E I O N I R M E L A L T UGH HAFT DON R O R ACTS GESTICULATE E C I R E GAG I T F N M SUN E FE H BAS I N EDUCATING WO VOCALISM MA D C A ALA B C MEAD M A C K I O E E UT POI HOBO Y A EL ABYSM A C DEALINGS MACRON MO A MAN R ISOLABLE SUFFUSED C NE MEM C TA G RAP OBIS O T D P C F T DAH GOD A E AIR E L LAC D R EPHOD KAE I I R CABINETRIES A N ICOSAHEDRONS A B CONCHS O OBA D A L P C C GEN MEN UP B PAINT A MM N DUI BABE H HAIRY TELEMARKETER B I C GOATISH NIL CLAY Y T A YIN U SATE U N I ART E E GOES TIC MODERNPENTATHLON NOSING ADMINISTRATIONS TRACE AMI DALES I A D H A S N C VIA F ORE F APE C S H S K POH S E FALSIFIABLE L AFFIRMATIVEACTION VALEDICTORIES T I S N E REG A N L WUD A R A TROPICOFCAPRICORN GORGONIANS LAB L I BACKCROSSES V E I ERA LEE KA D I Y C BONGO E C E C EAGER CUSPATE O N ANADEMS KOHL C RAID HAD TIS M A N M H I BATE D S I I I I LAT T OAR E L A O E I N T BRYCECANYONNATIONALPARK APPALLING FRACTIONALLY K AGE UTA ICE B ASH TAPE U O SI L T C B A IMPOVERISHMENTS L BIOS ONSTAGE B O I O PLED C EWE A N U O US AAL T R B WHO ABO I H AND T E BIOSOCIAL B CHOREA E E N CAW S EF EASE C E D UDDERS E SPEAR R TEREPHTHALICACID S UKASE SOM R S H S |
The Corresponding Solution

|
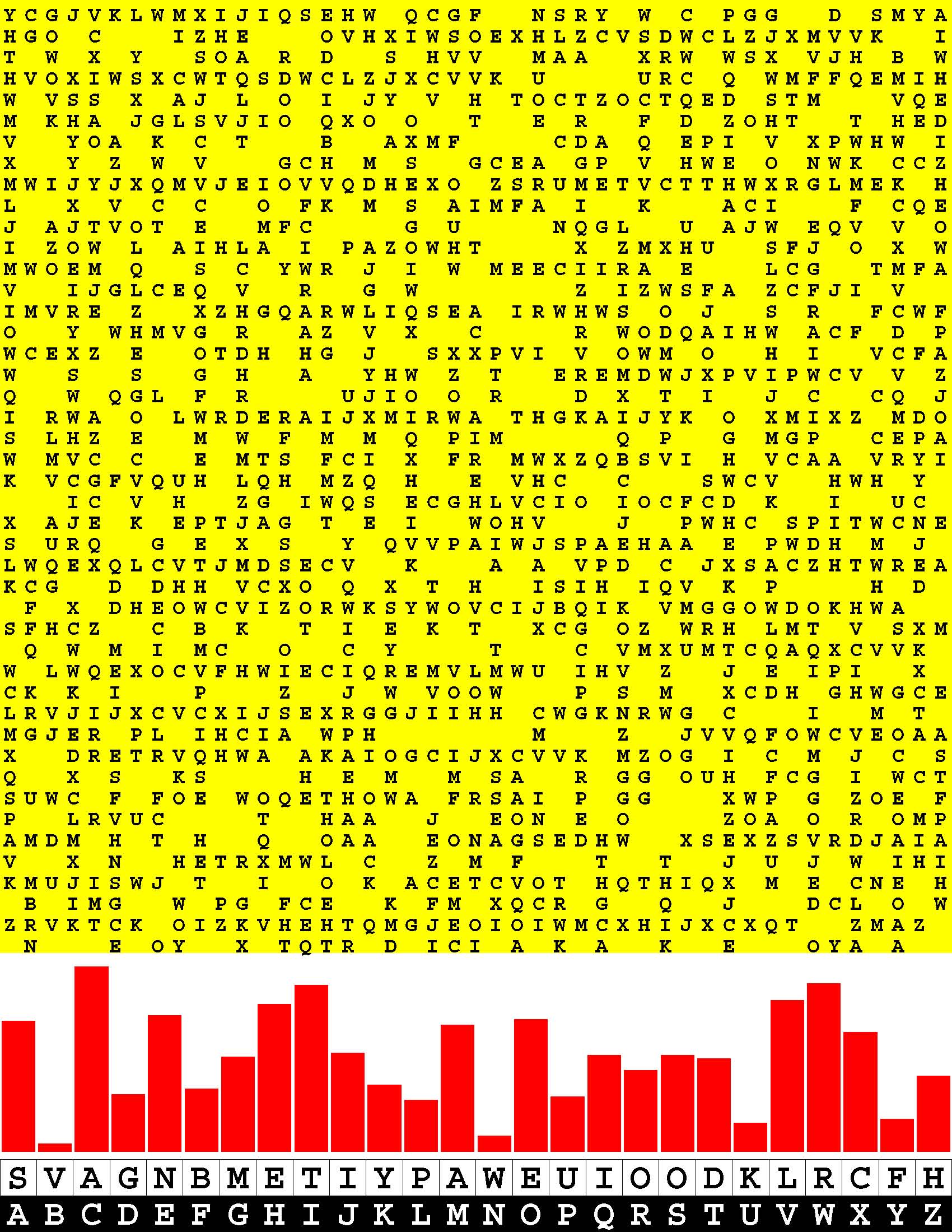
|
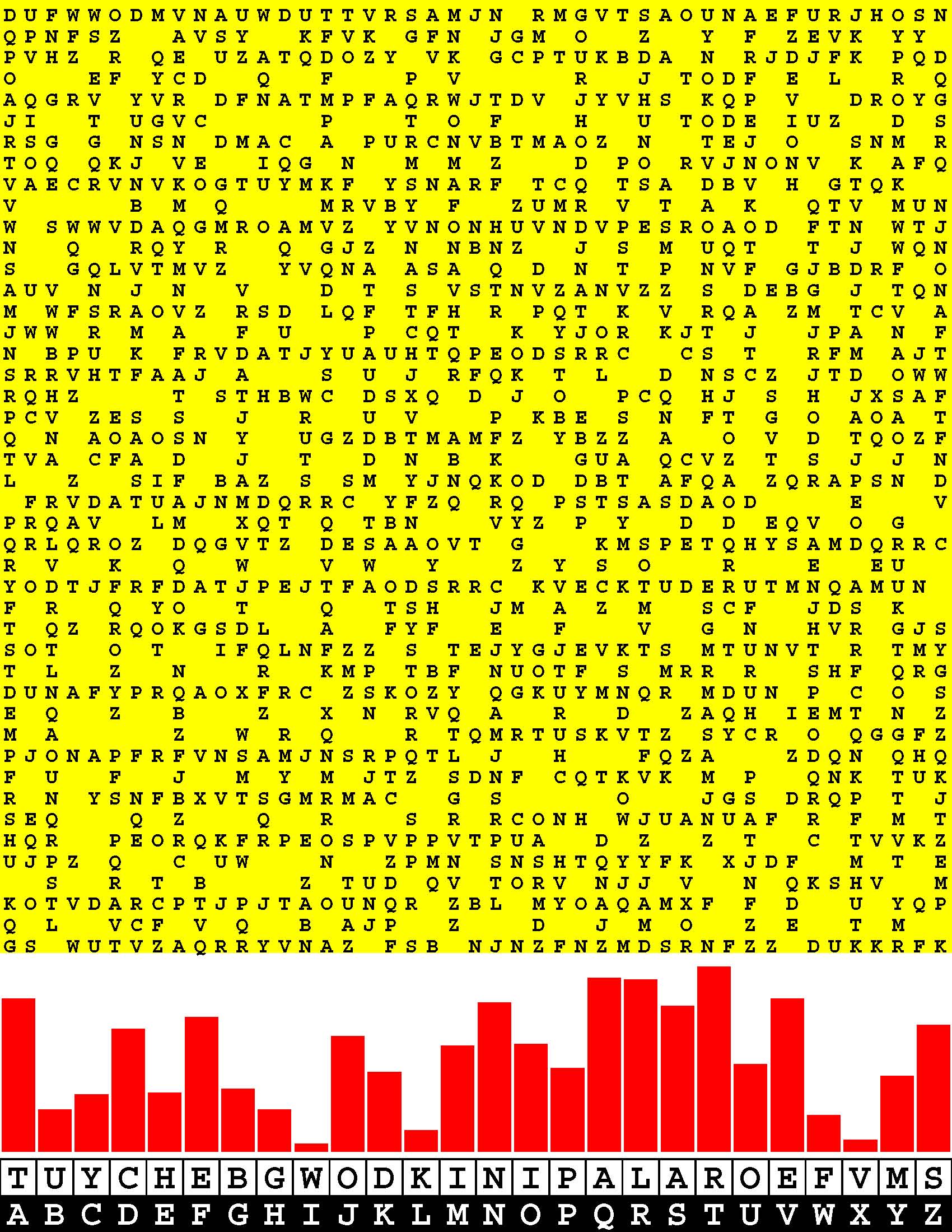
|
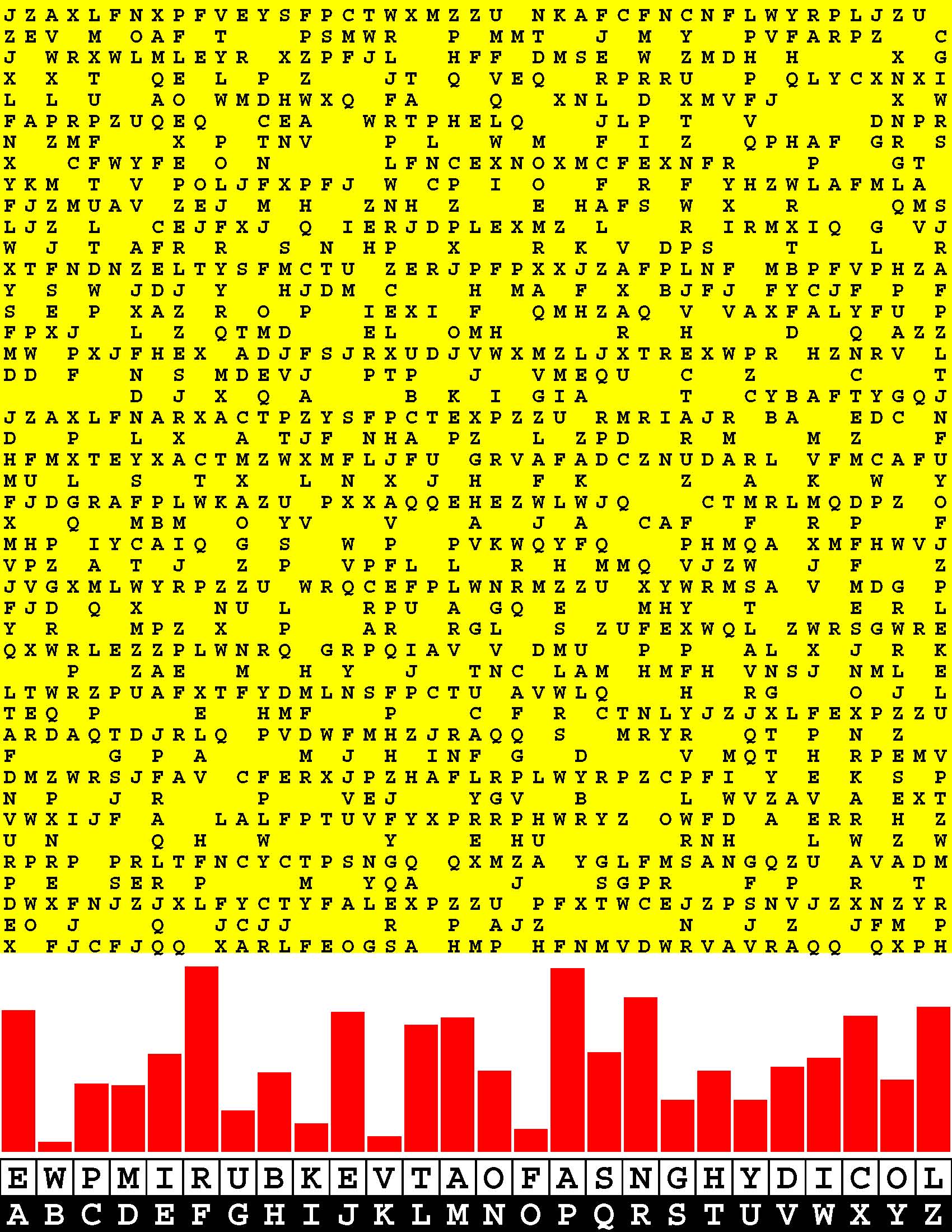
|
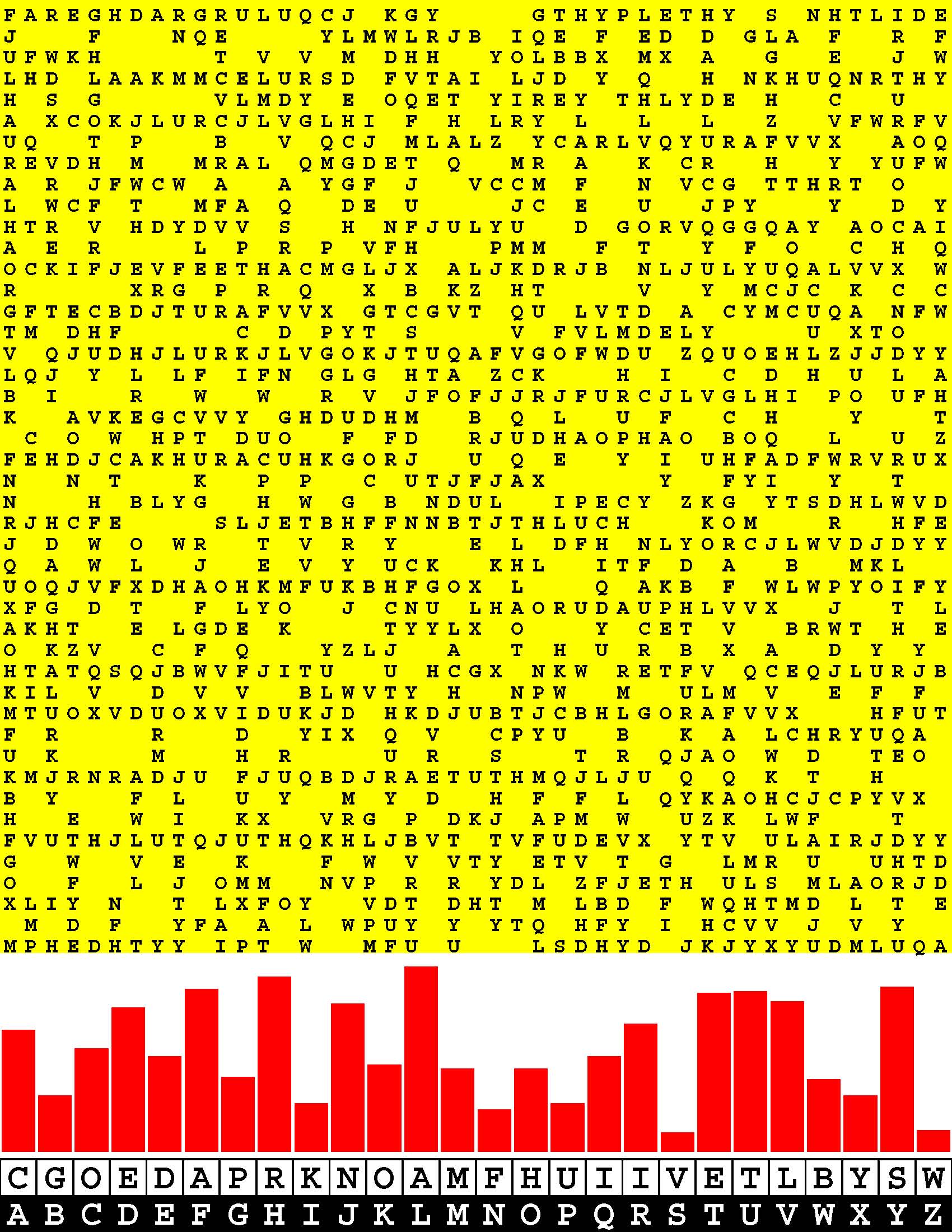
|
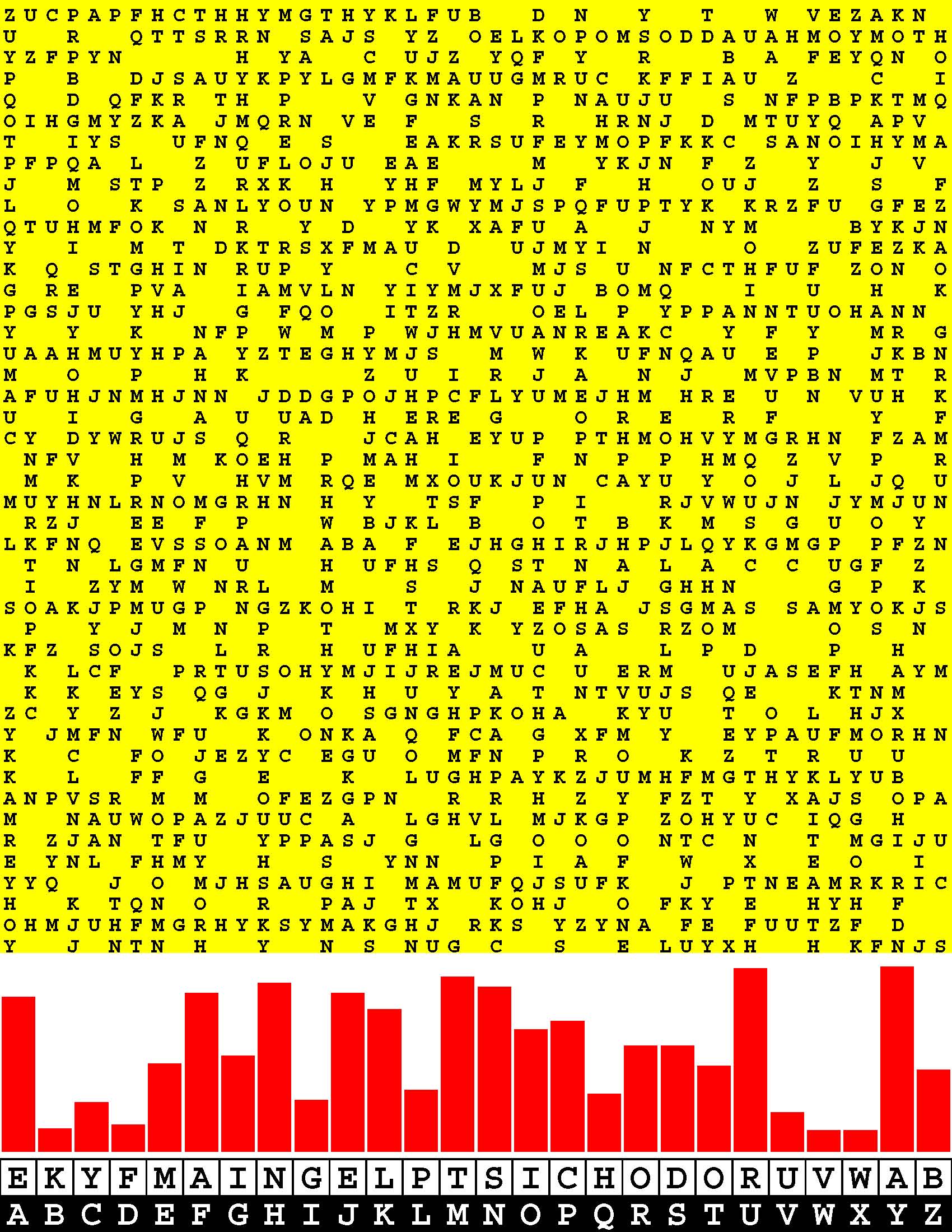
|

|

|
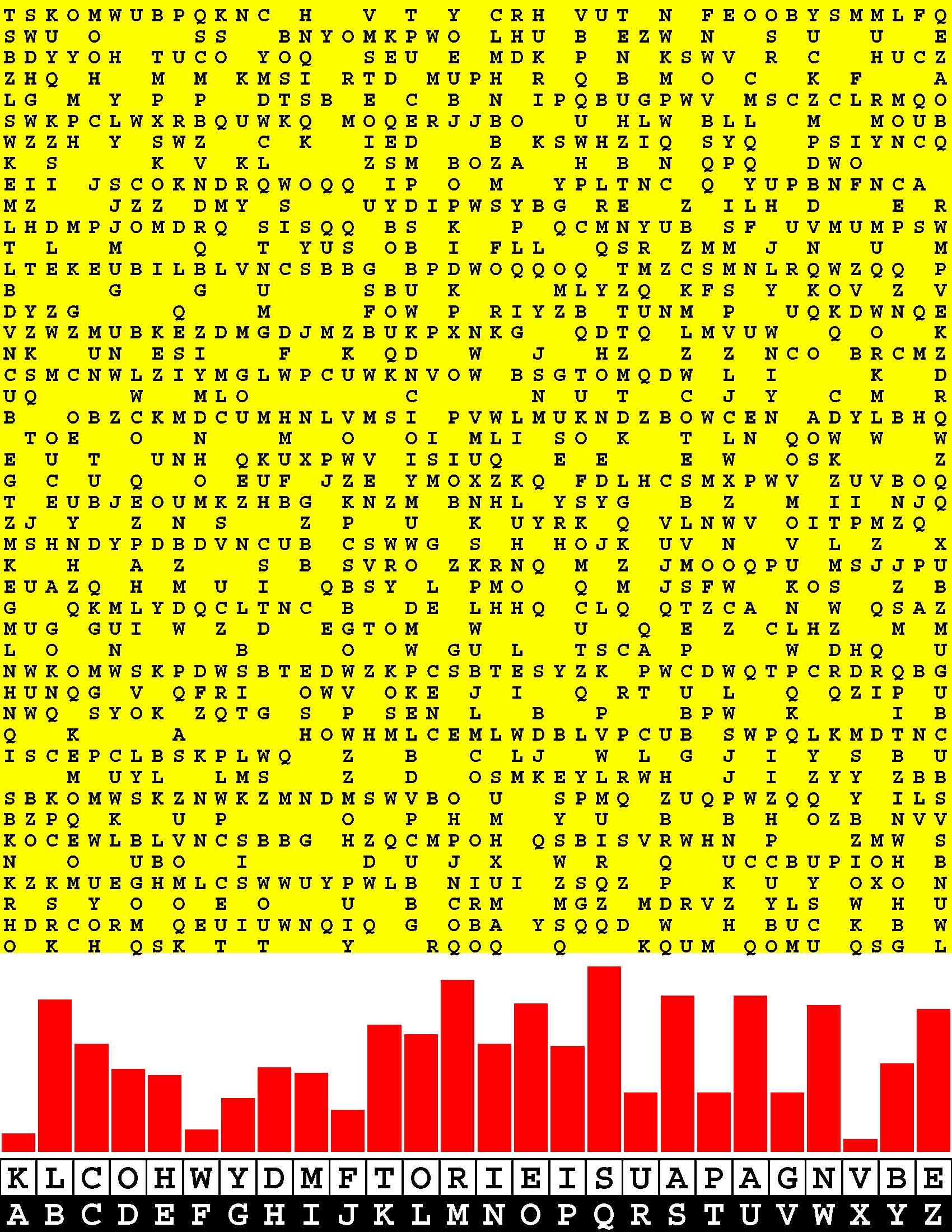
|
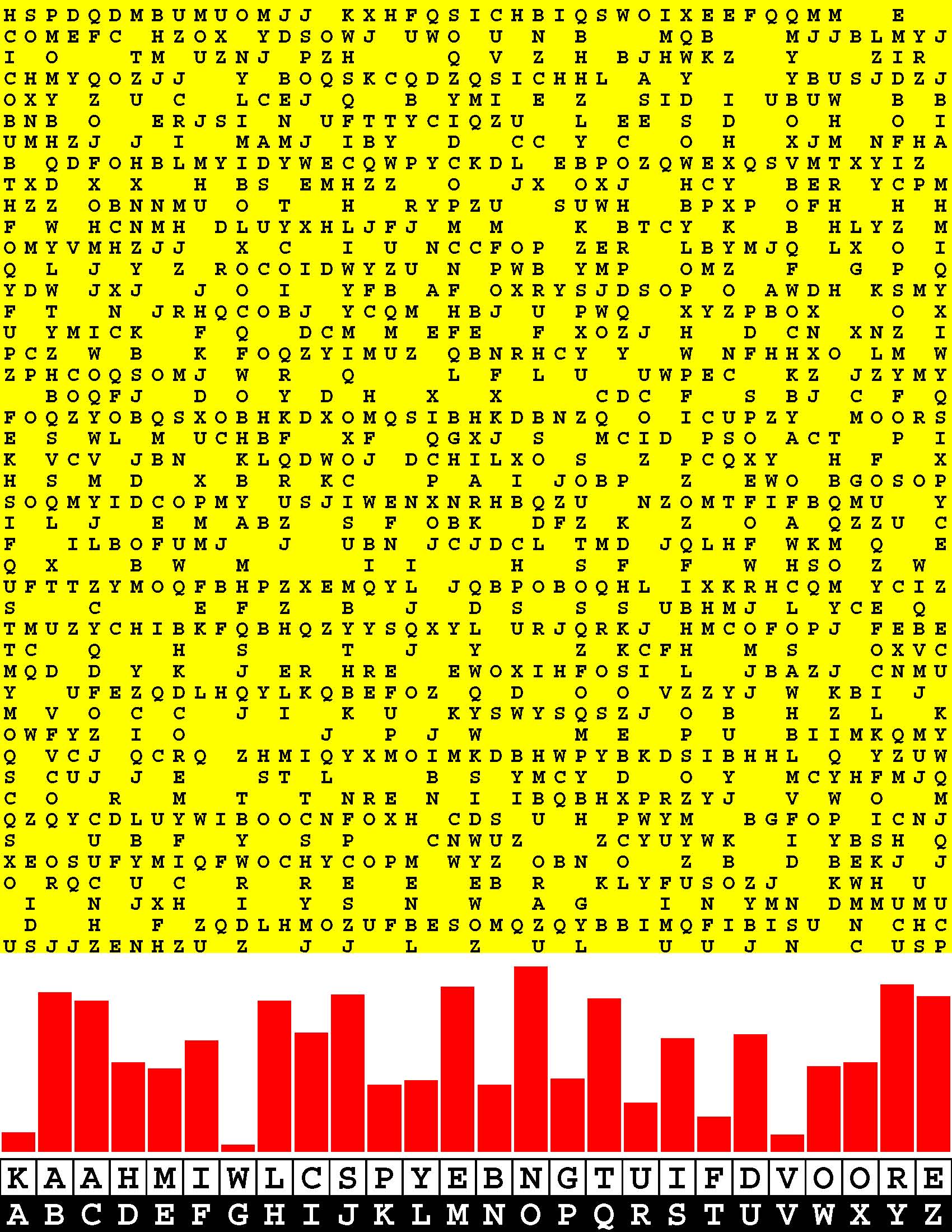
|
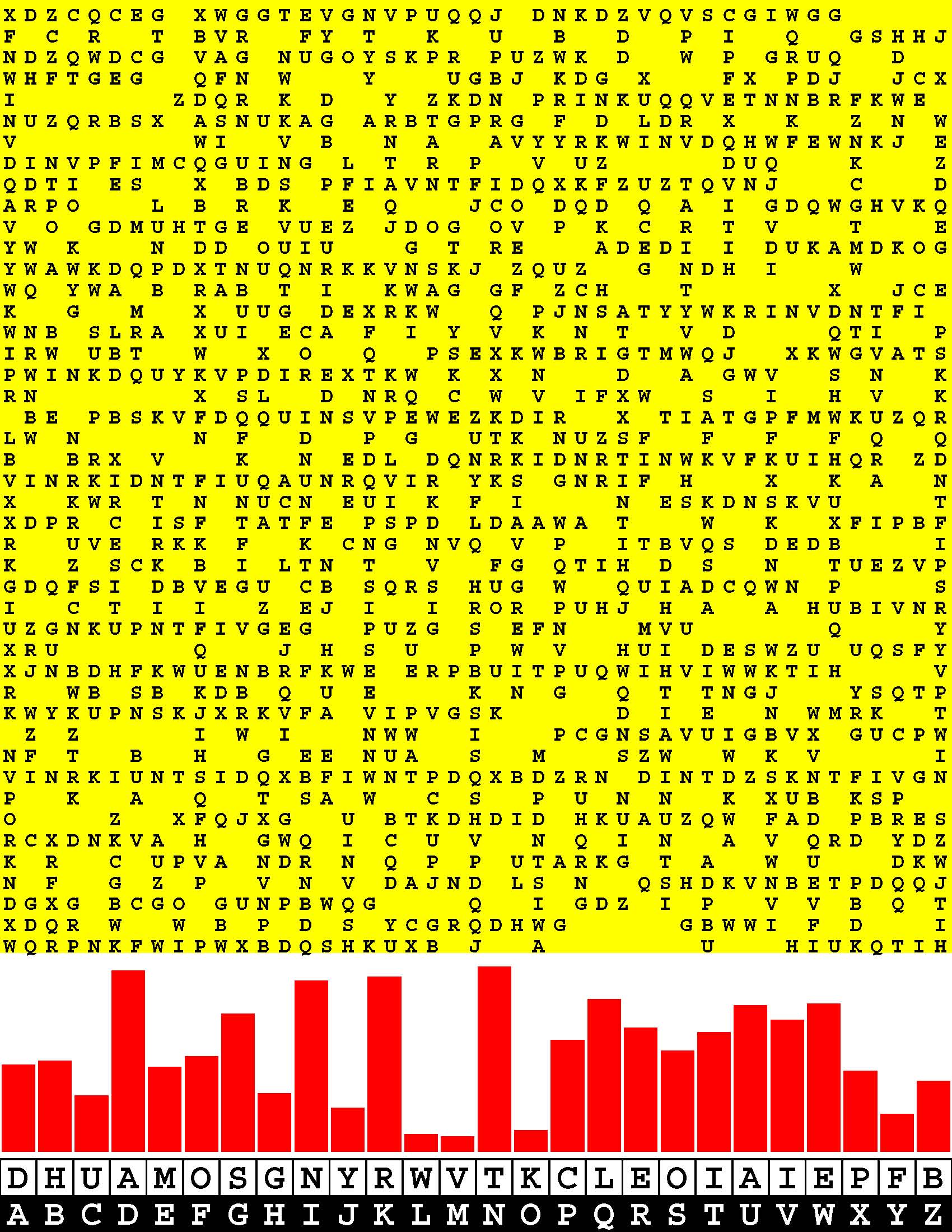
|

|
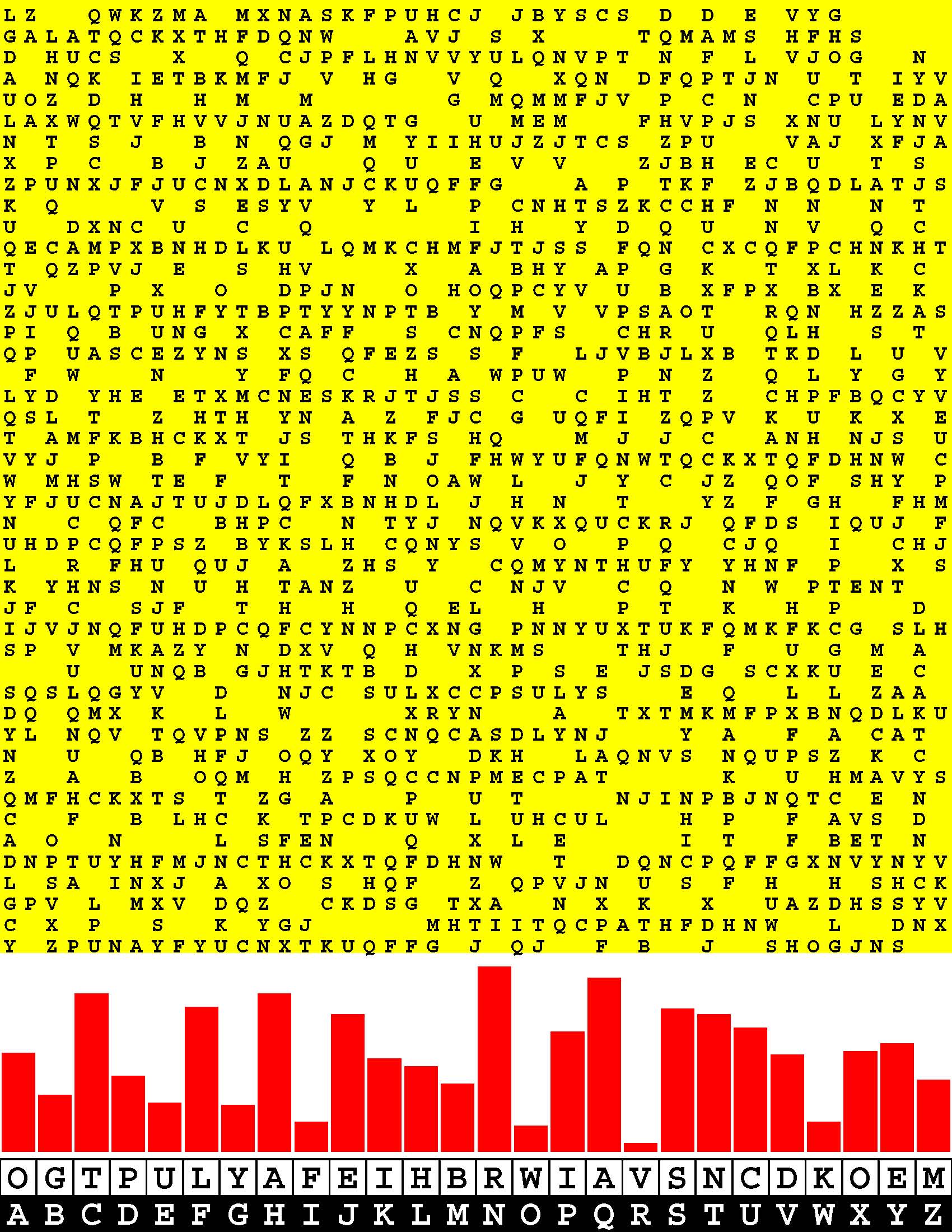
|
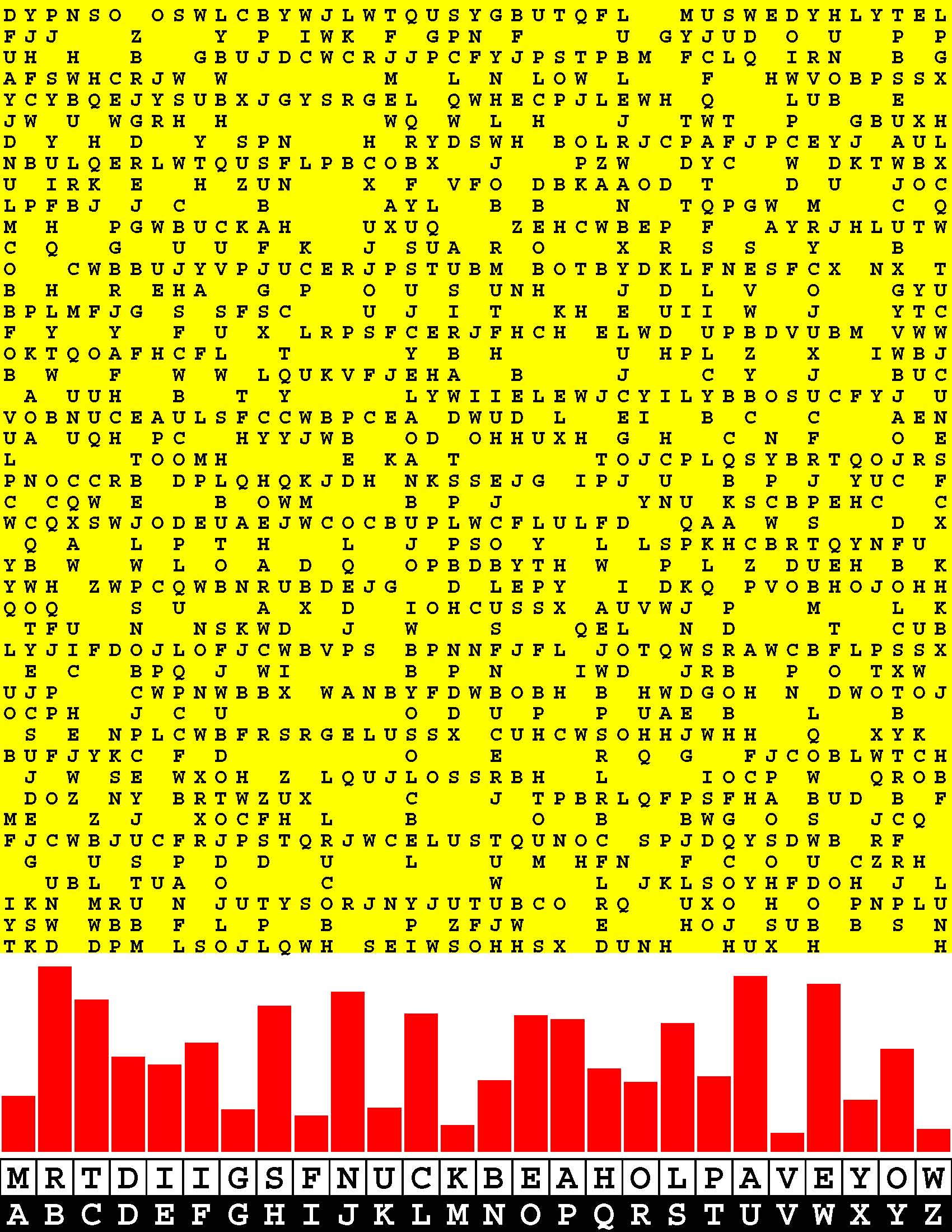
|
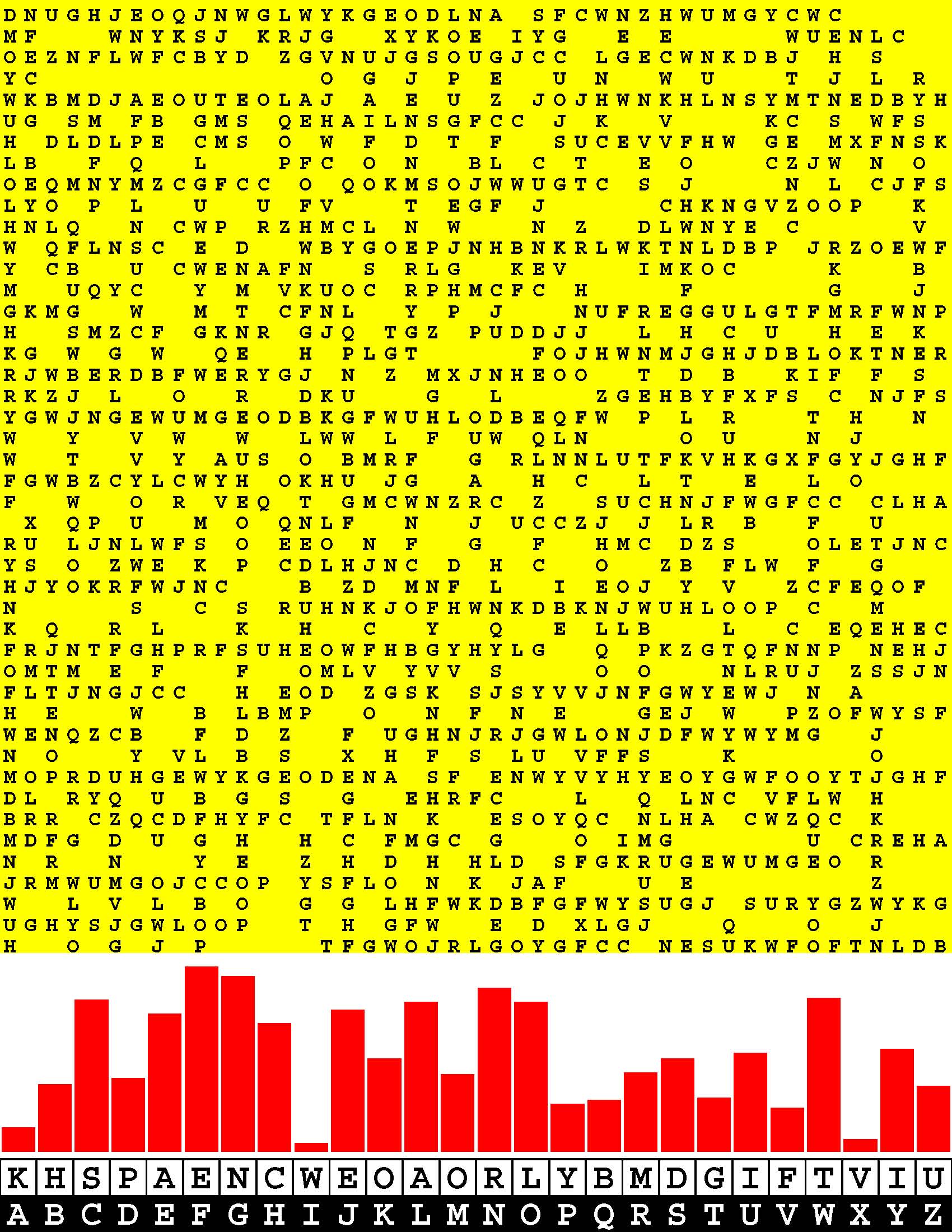
|
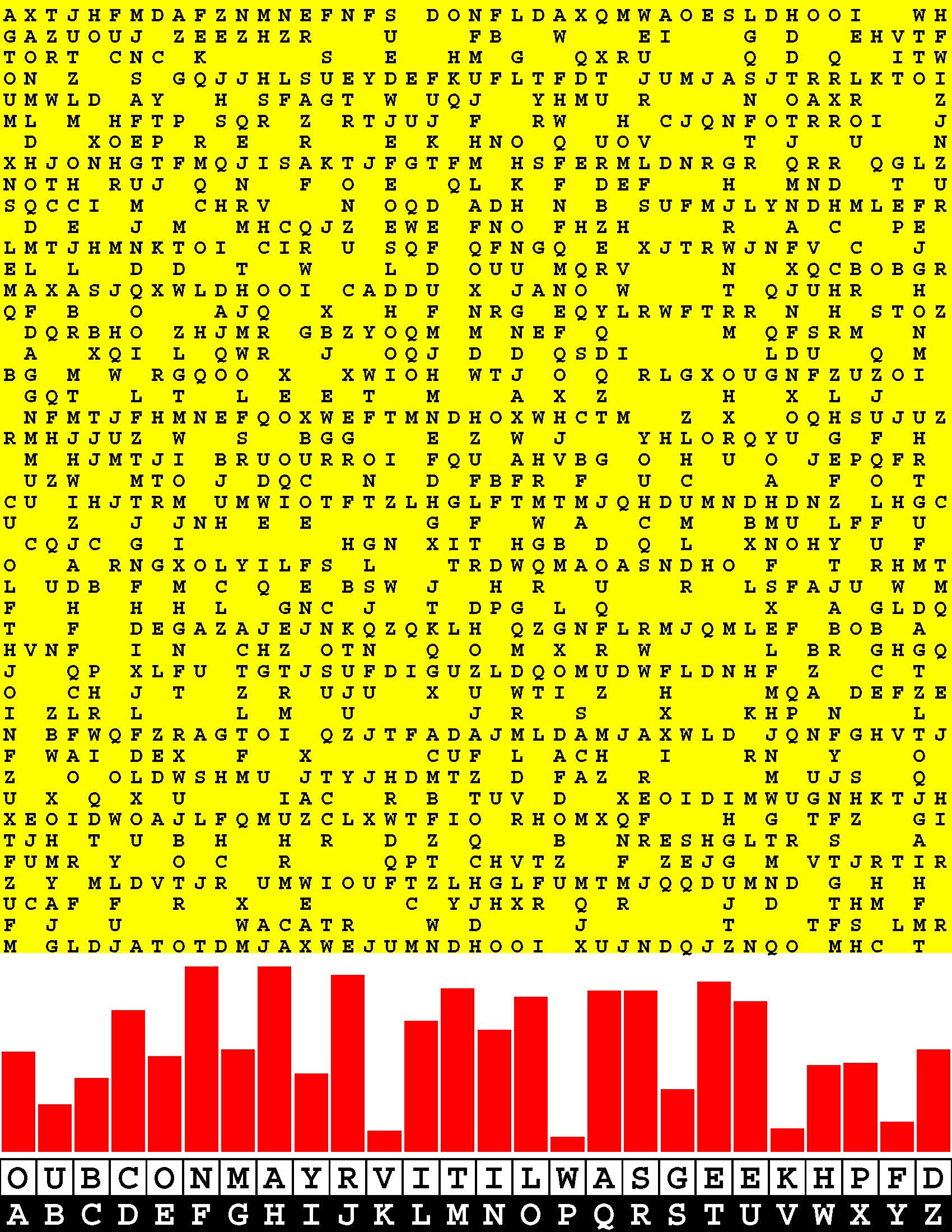
|
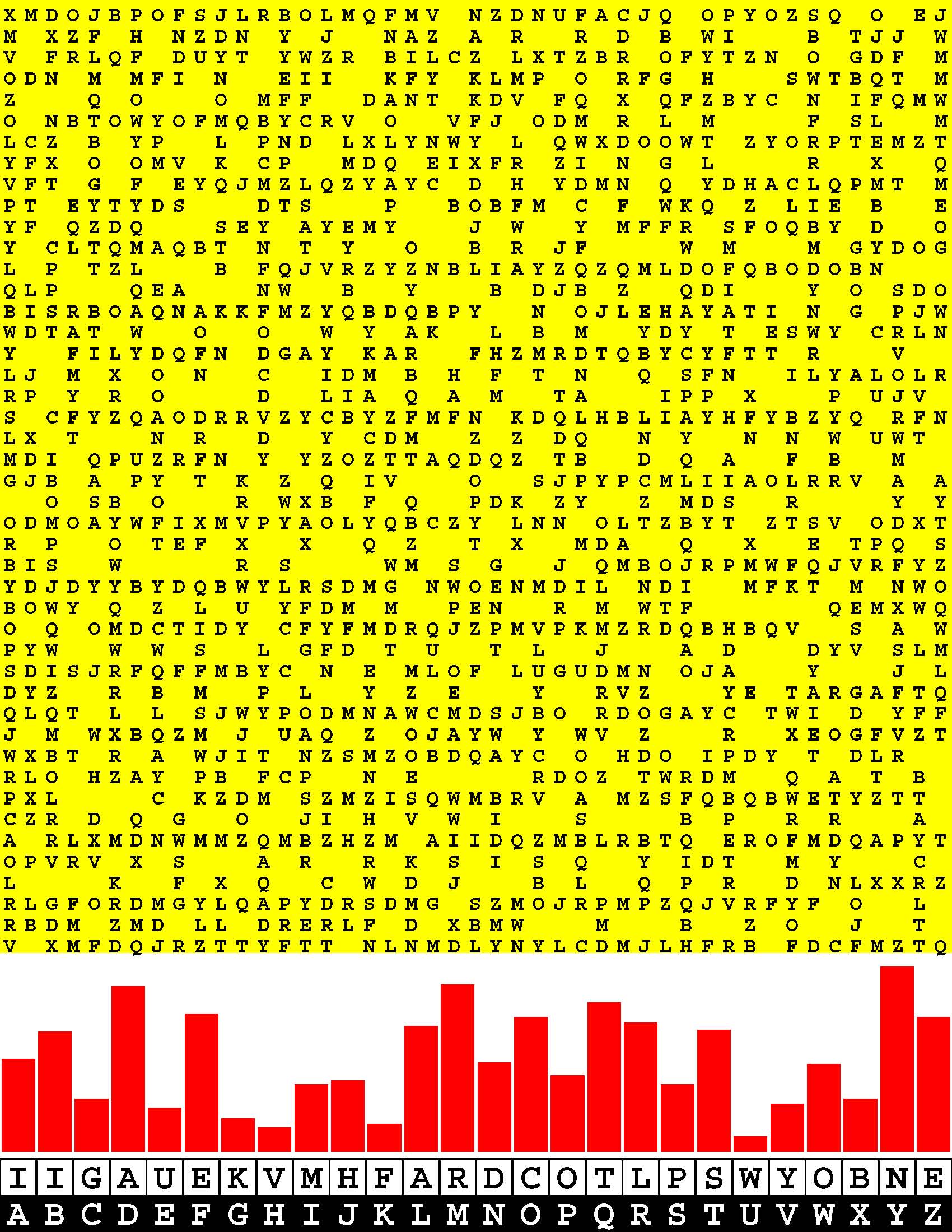
|
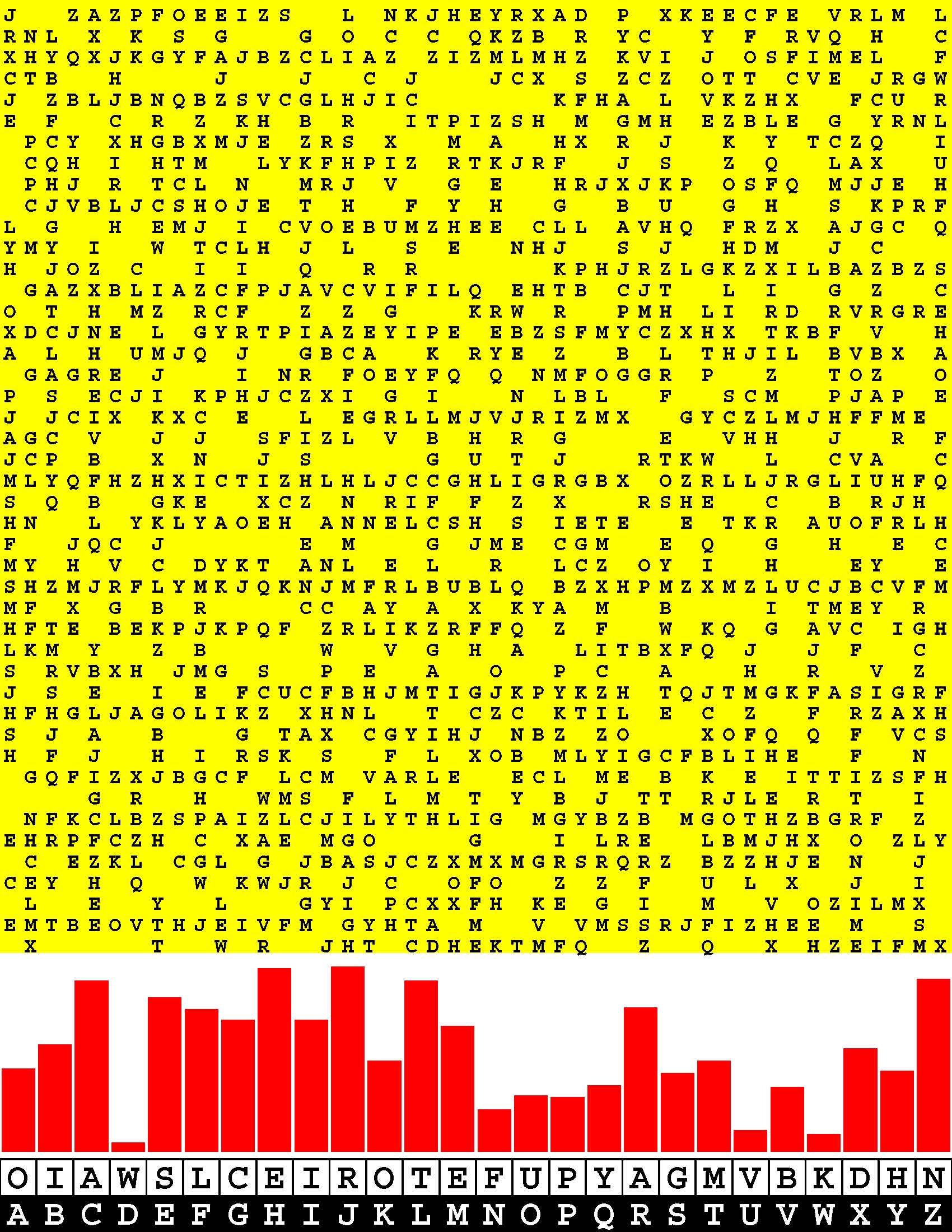
|

|
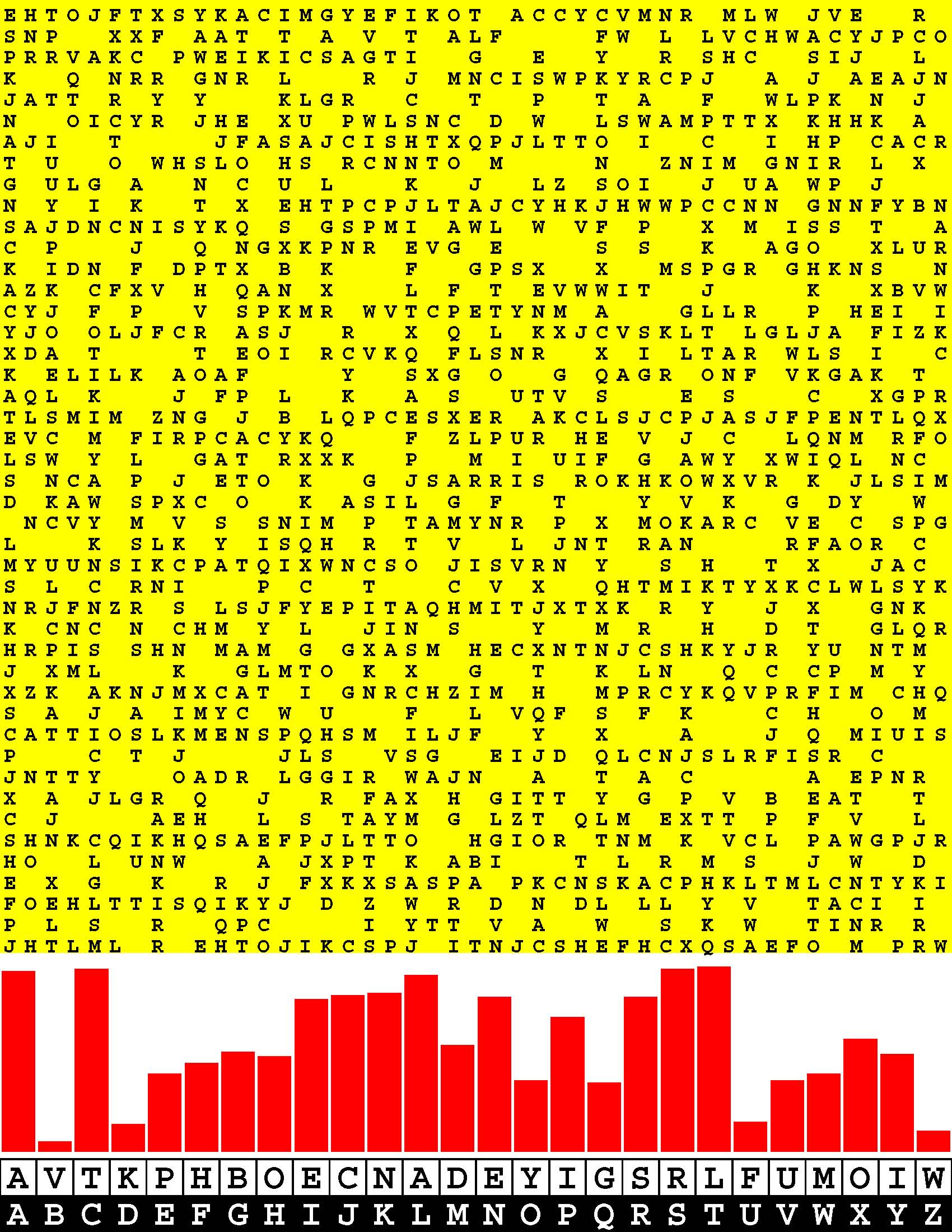
|
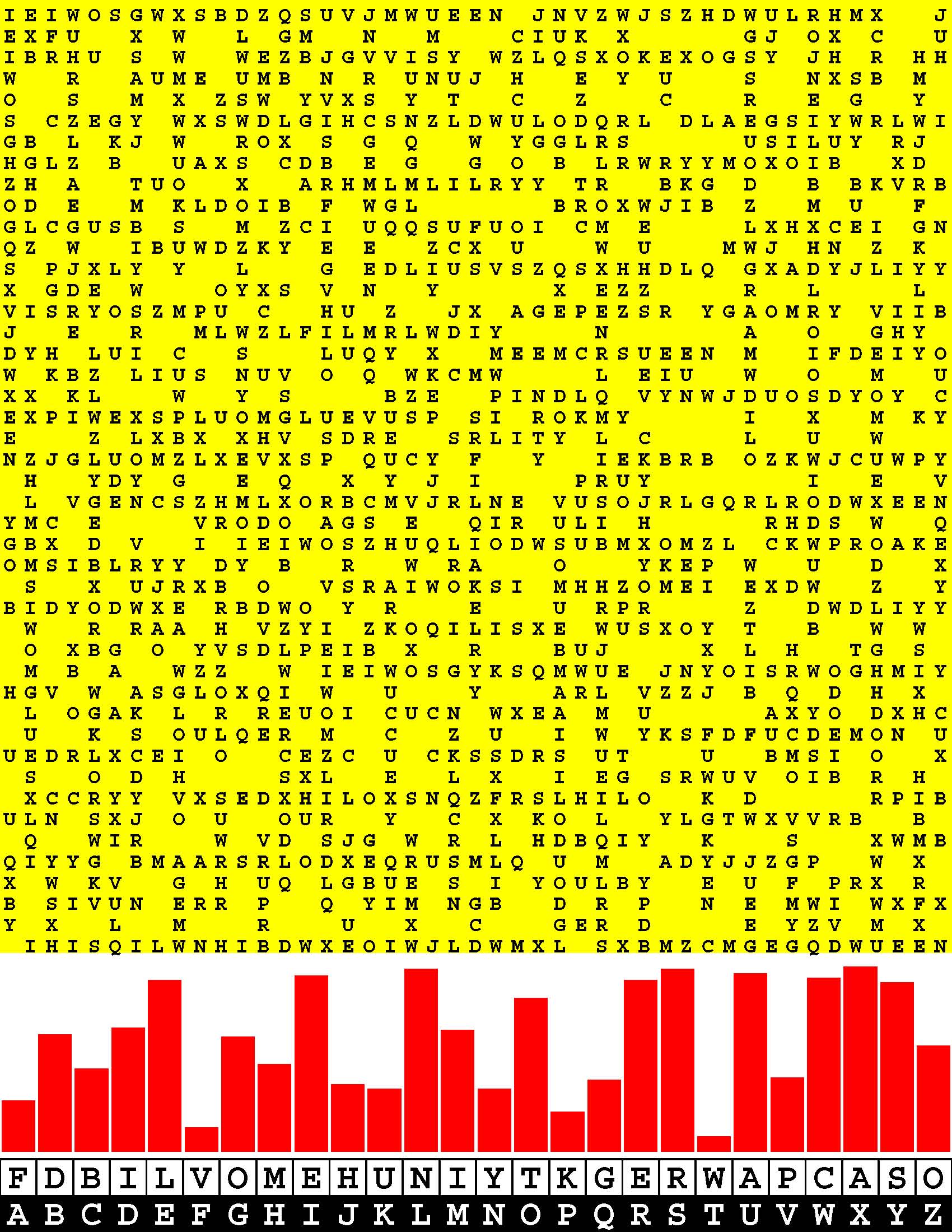
|
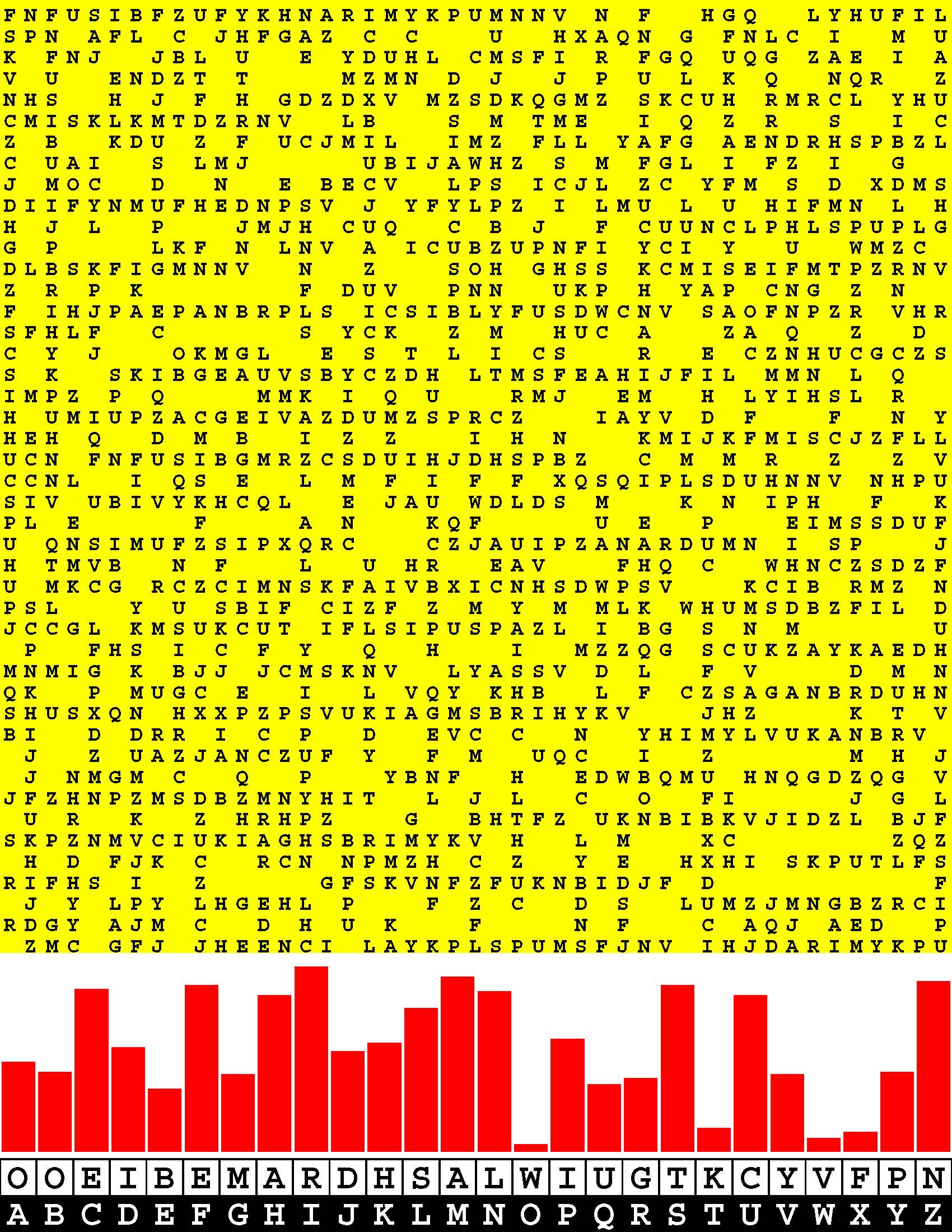
|

|
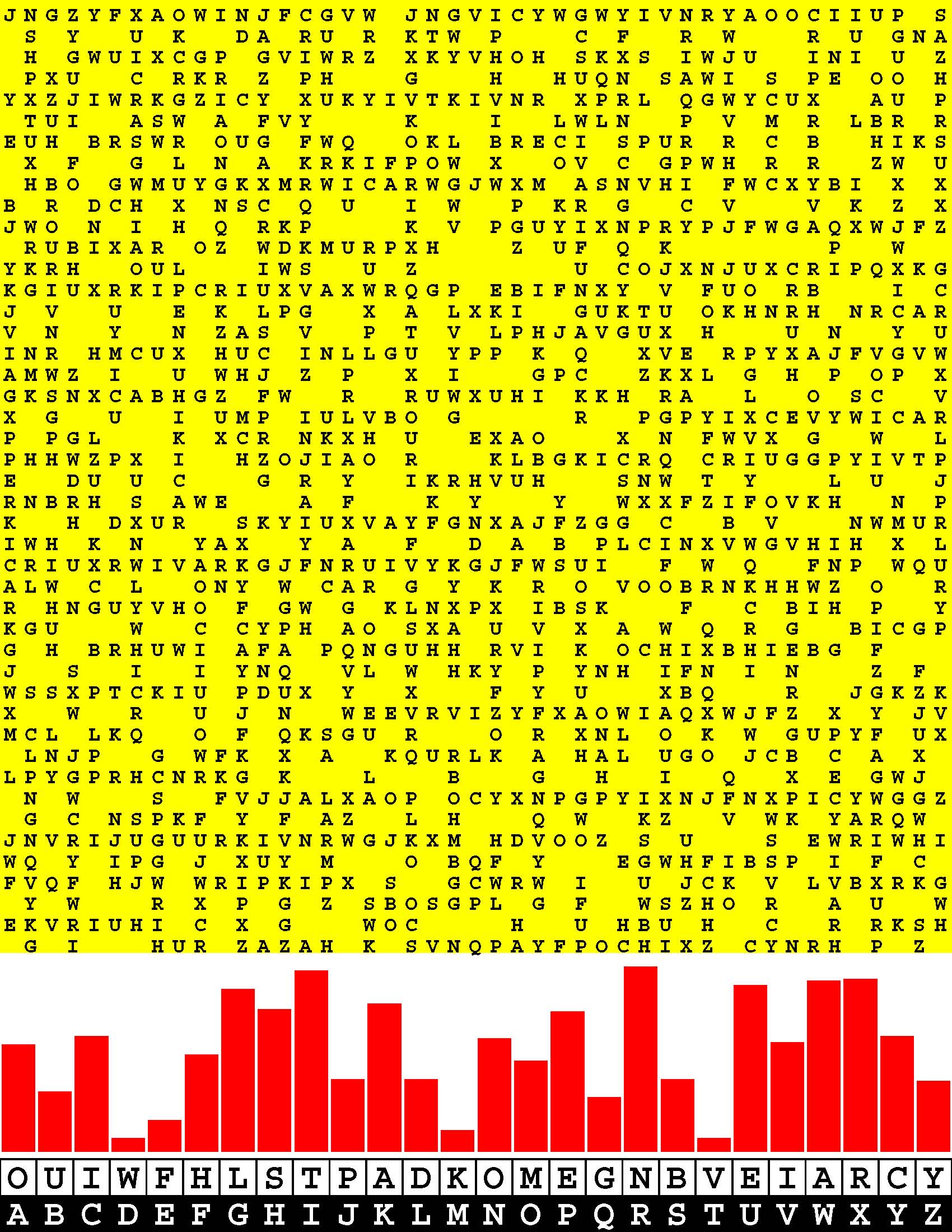
|
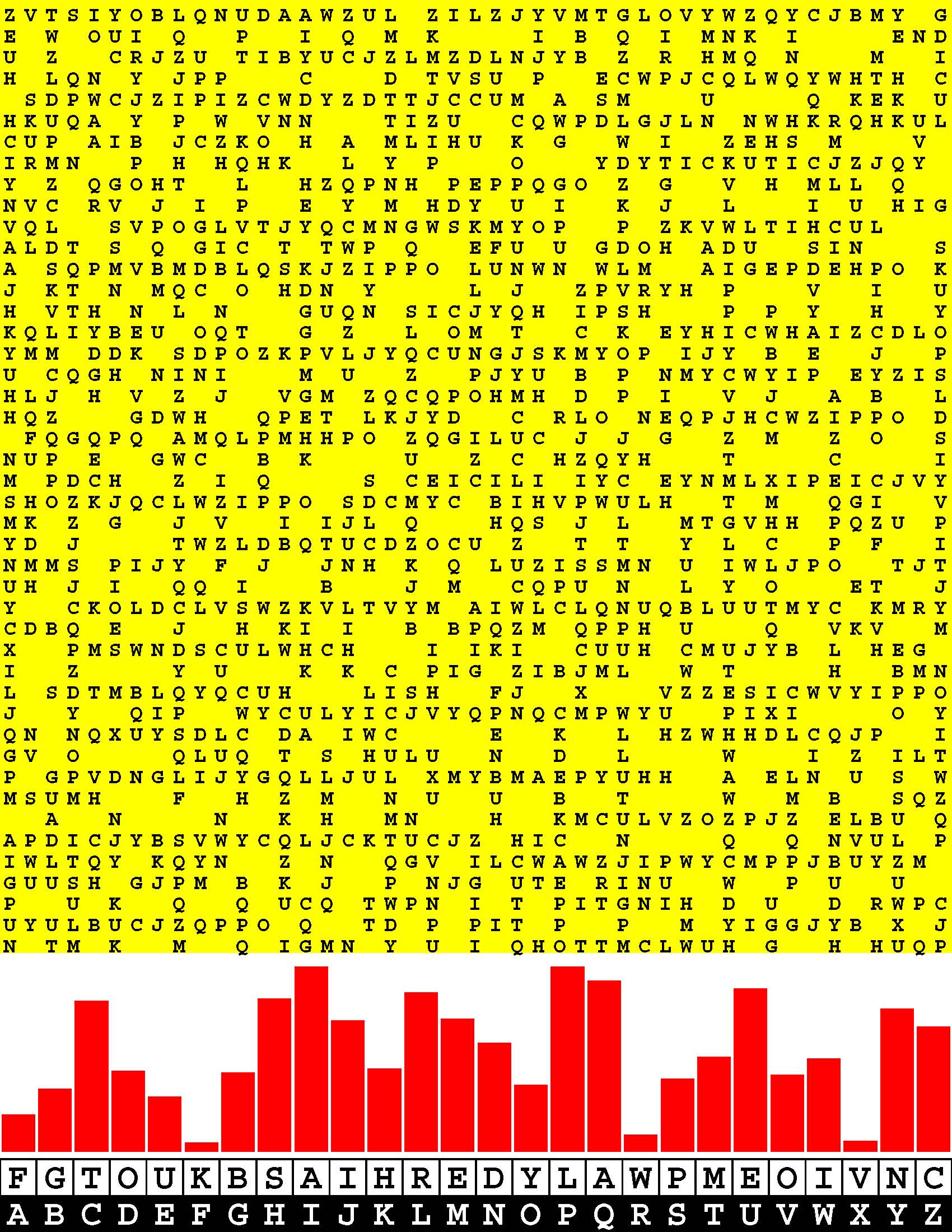
|
146,853 Homophonic Prepper-Sums-Puzzles by Francis Gurtowski
|
This is yet another serious, serious series of 999 books created by Francis Gurtowski.
The prolific author is an authentic, ancient coder, going all the way back to IBM Poughkeepsie (Building 705, no less, second floor) and the heyday of OS/360, Robert Rex Seeber Jr. and the horizontal-microcoded System/360 Model 50, coding pads and the coding-pad veto, punch cards and keypunch machines, and self-modifying code. Francis Gurtowski is also a self-styled Henry Ford of contemporary, do-it-yourself, print-on-demand, book publishing. Henry Ford is synonymous with the assembly line, a perfected process for swiftly turning out a series of ingenious, finished products in a foolproof, mechanically-efficient manner. Once again, each of these sequels takes full advantage of (Amazon) Kindle Direct Publishing's twin, generous, upper limits of 590 bound-and-paperbacked, 8.5x11-inch pages. The concept is simple enough. A Homophonic Prepper-Sums-Puzzle is a counterpart of a crossword puzzle with certain cosmetic deviations, namely (a) the free-range layout of the resulting niches of the puzzle was not predetermined by an articulated grid, (b) the clues, such as they are, which is not much, are statistical rather than literary, and |
(c) the puzzles are not topical whatsoever; the common theme of one and all is addition per se.
Replace each letter of the alphabet with a decimal digit such that (a) the respective sums of the digits in the multiple-place niches situated across the grid are mutually equal to some N1 total and at the same time (b) the respective sums of the digits in the orthogonal, multiple-place niches situated down the grid are mutually equal to some different N2 total. For example, 1911699 obviously does not equal 369919, but both 1+1+9+1+1+6+9+9 and 3+6+9+9+1+9 equal 37. Similarly, 11842199 does not equal 711899, but both 1+1+8+4+2+1+9+9 and 7+1+1+8+9+9 equal 35. The plain text here is a solution to a novel scheme of crossword puzzles such that it is not words per se but instead numerical summations which are crossed across and down. Be advised that in order to make your decryption experience even more challenging - and thus much, much, much more rewarding - than it would ordinarily be, there is a catch in my approach to my separate encryptions of the 15x15-square, open-plan crosswords. |
Not content to simply substitute precisely one ciphertext letter per plaintext letter (decimal digit), I instead more or less arbitrarily substitute one or more ciphertext letters for each plaintext letter (decimal digit).
So I do not use a simple substitution cipher. I instead resort to what is called homophonic coding. According to Merriam-Webster, a homophone is one of two or more words pronounced alike but different in meaning or derivation or spelling - such as the words to, too, and two. Conventual homophonic coding not only camouflages but also distorts the patented statistics of the English language, which are common knowledge amongst Scrabble aficionados. The decimal-digit statistics of arbitrary sums are yet to be patented. With a simple substitution cipher, if the respective frequencies of the plaintext crossword approximate normality then the same will be said of the ciphertext crossword - only spread differently. A simple substitution cipher is comparatively a piece of cake to attack with paper and pencil. Homophonic encoding, on the other hand, is absolutely a beast. |
A Specimen of the Ciphertext
Across
|
Down
|
The Corresponding Relative Frequencies
Of The Letters Of The Alphabet In A Census
Of The Said Specimen Of The Ciphertext
|
The Corresponding Specimen Of The Plaintext
Across
|
Down
|
The Corresponding Solution

|

|

|

|

|

|

|
Learn to Color, Color to Learn - Homeschool Workbooks by Francis Gurtowski
|
This is yet another serious, serious series of books created by Francis Gurtowski.
The prolific author is an authentic, ancient coder, going all the way back to IBM Poughkeepsie (Building 705, no less, second floor) and the heyday of OS/360, Robert Rex Seeber Jr. and the horizontal-microcoded System/360 Model 50, coding pads and the coding-pad veto, punch cards and keypunch machines, and self-modifying code. |
Francis Gurtowski is also a self-styled Henry Ford of contemporary, do-it-yourself, print-on-demand, book publishing.
Henry Ford is synonymous with the assembly line, a perfected process for swiftly turning out a series of ingenious, finished products in a foolproof, mechanically-efficient manner. |
Calling all parents, grandparents, teachers, and school Principals.
Buy this educational series of self-teaching, coloring books for your children, grandchildren, and students. Sit your child down with this series of over a hundred coloring books. It is enough to make you want to grab a fistful of colored pencils and have at it yourself. |

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
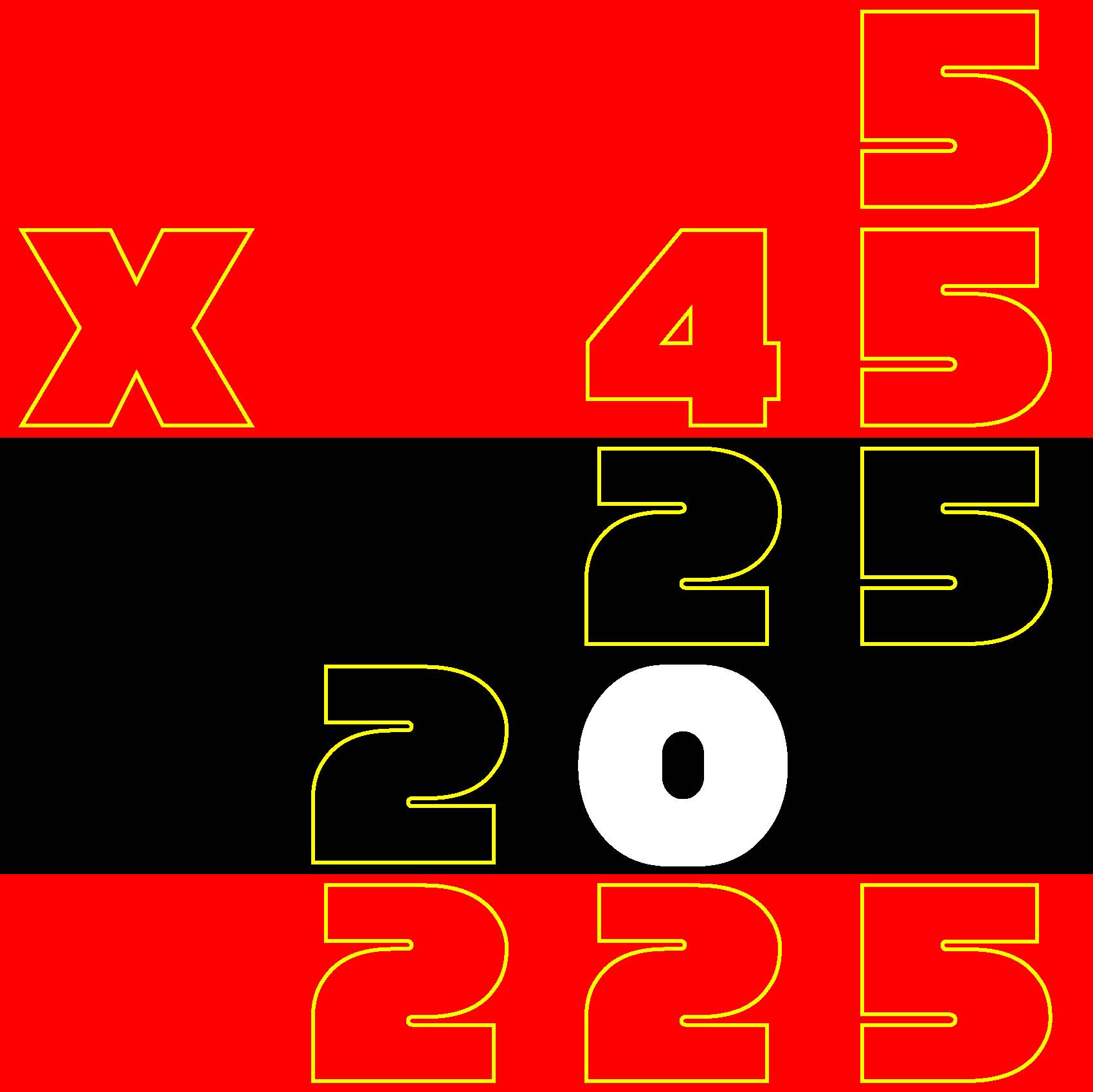
|

|

|

|

|

|

|
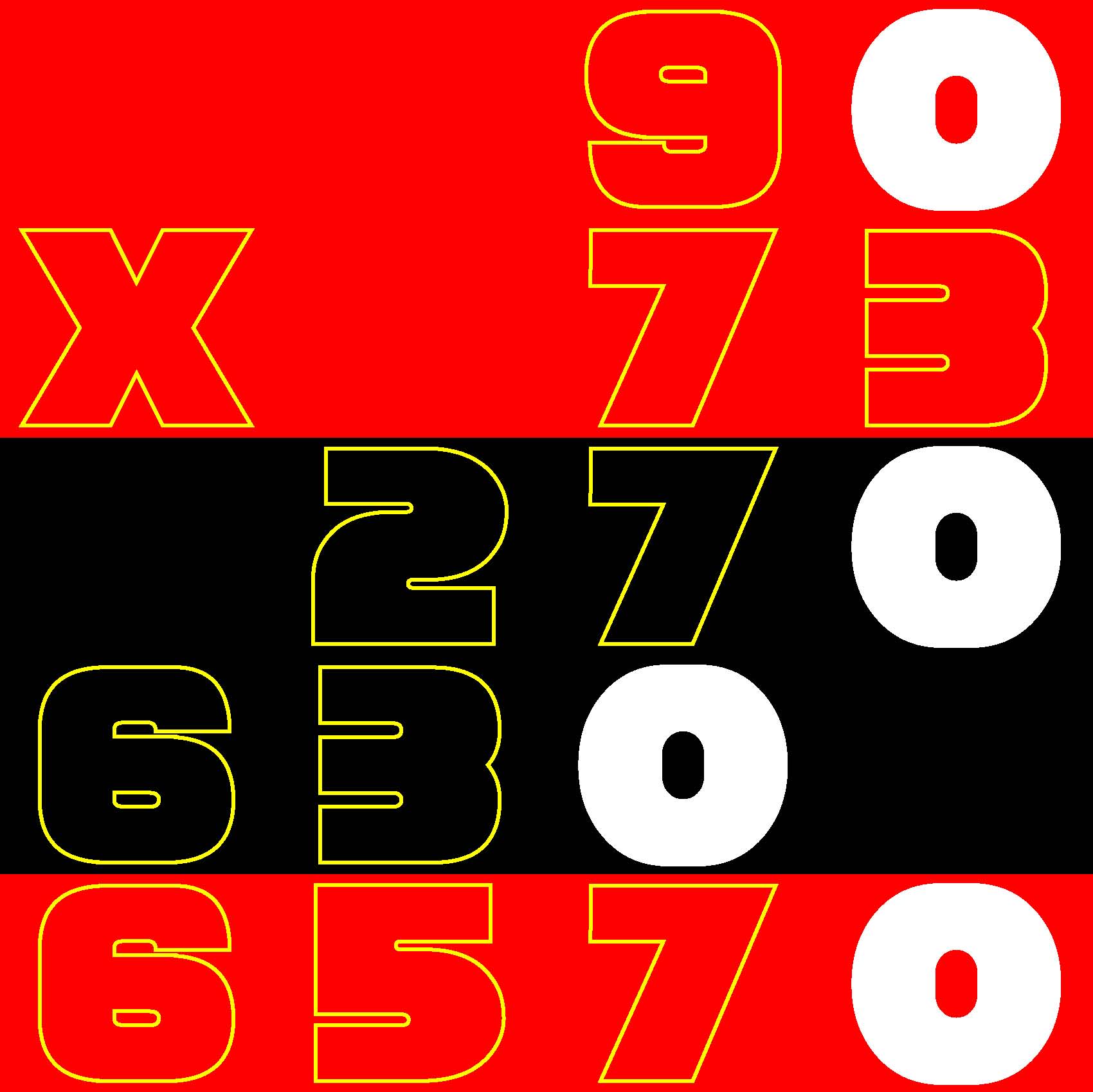
|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
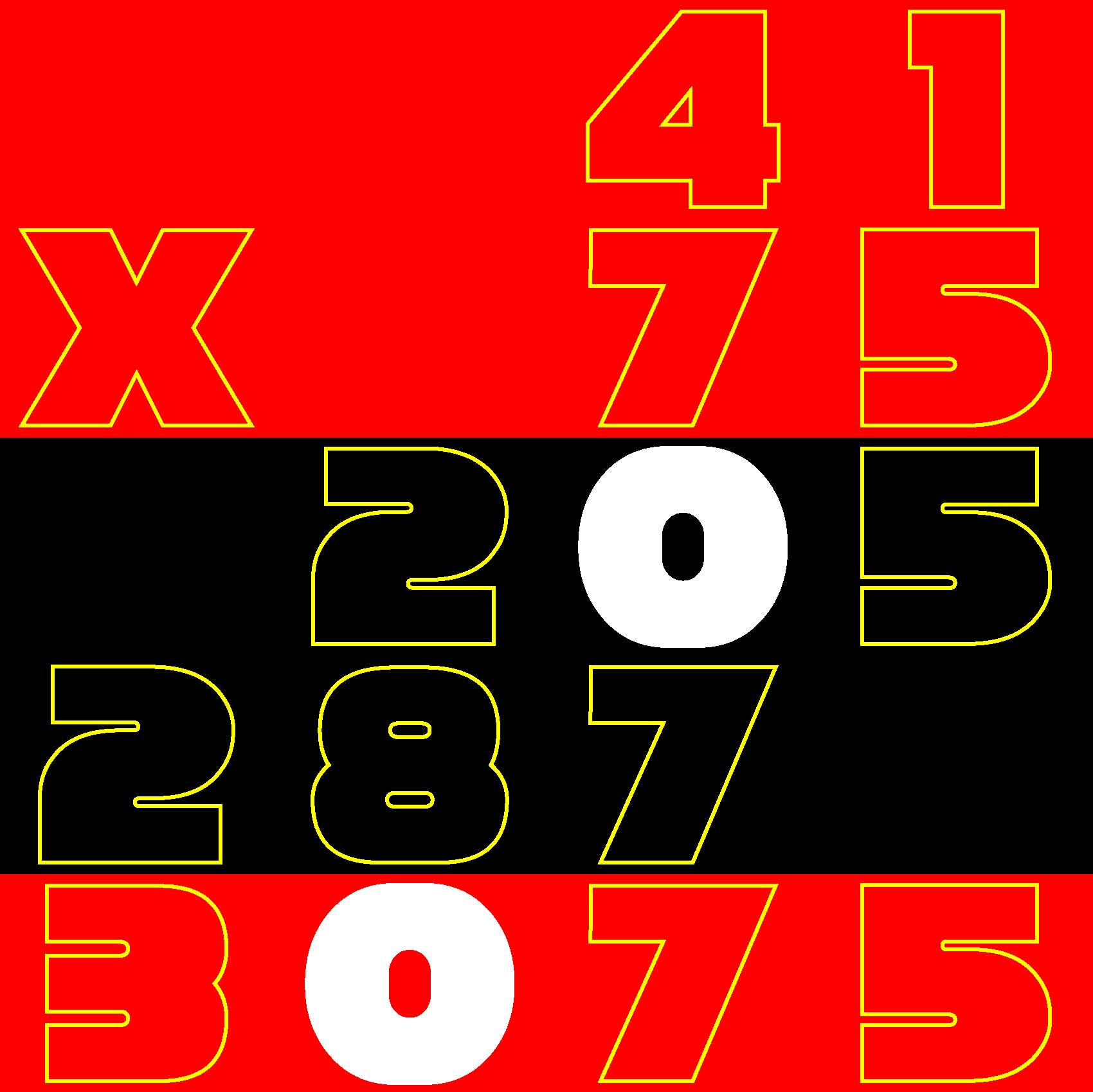
|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
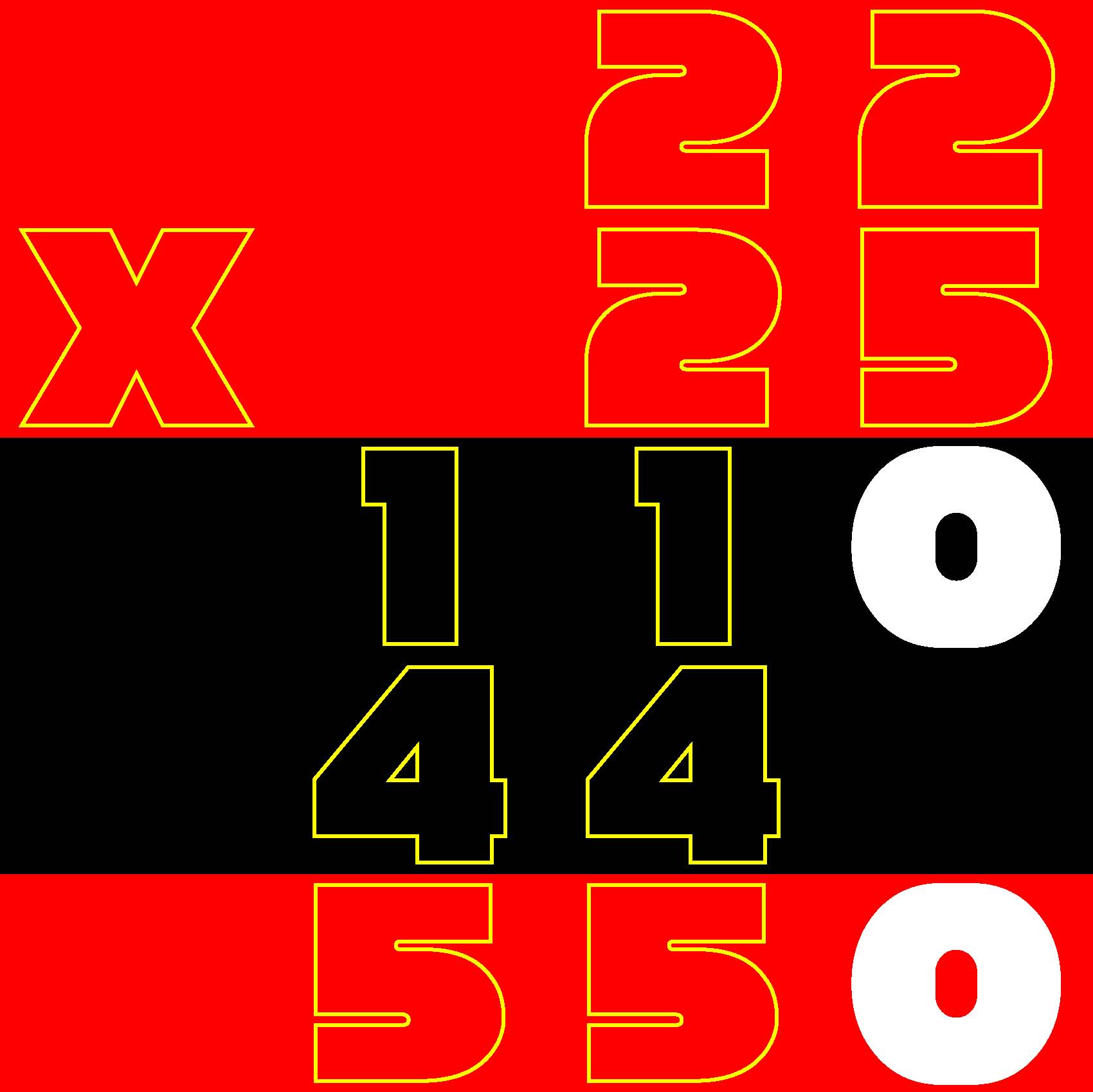
|

|

|

|
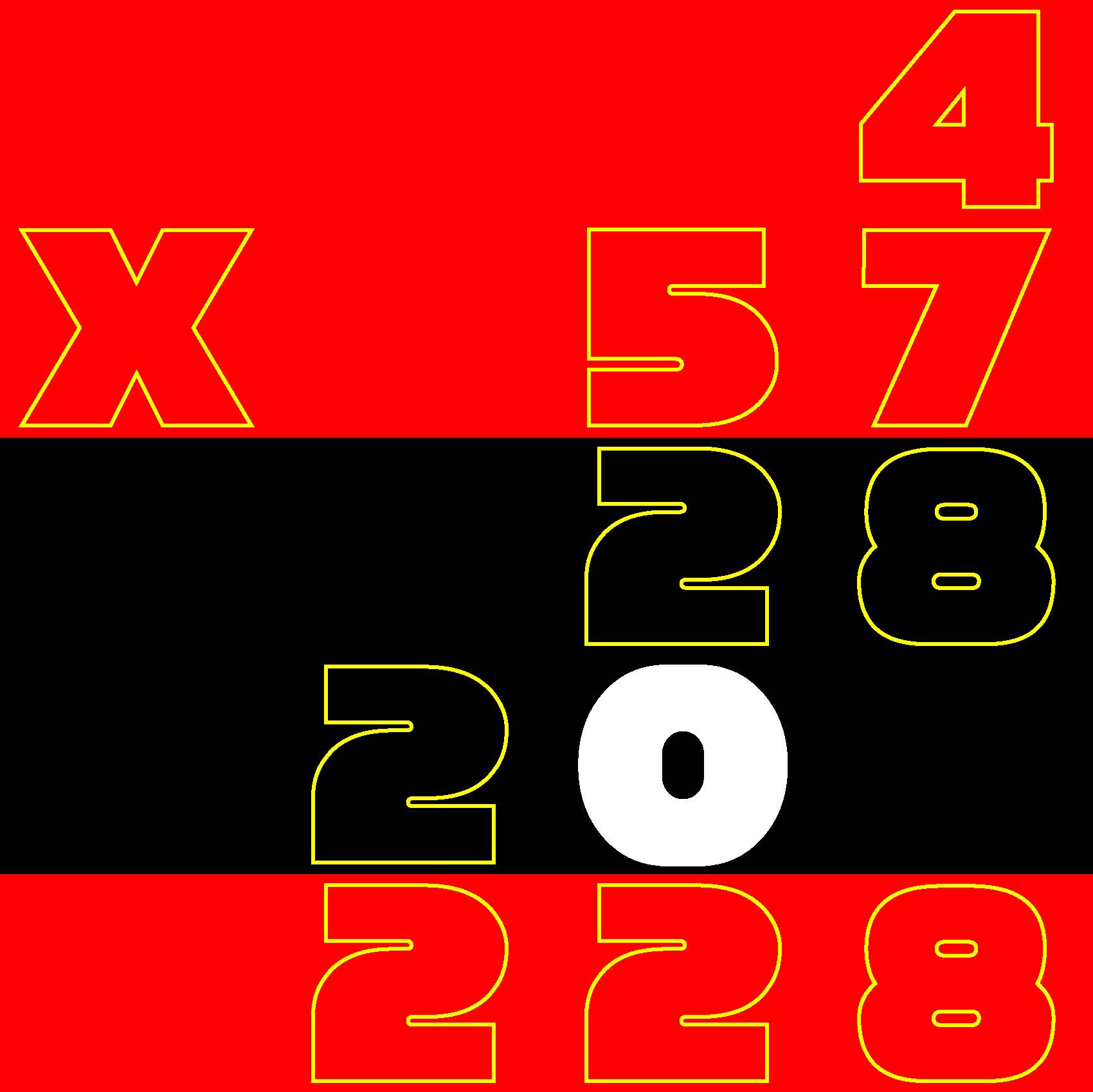
|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
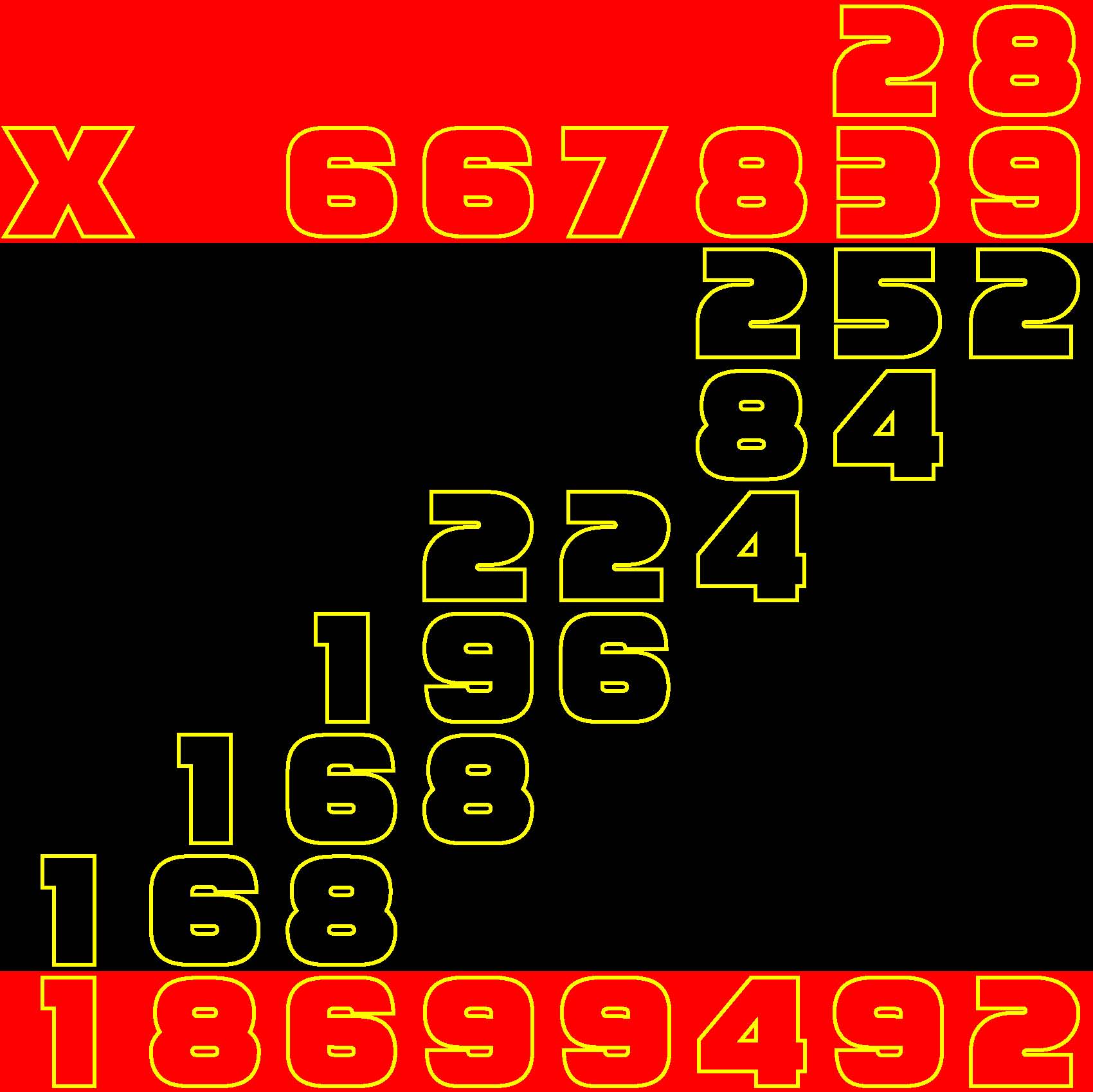
|
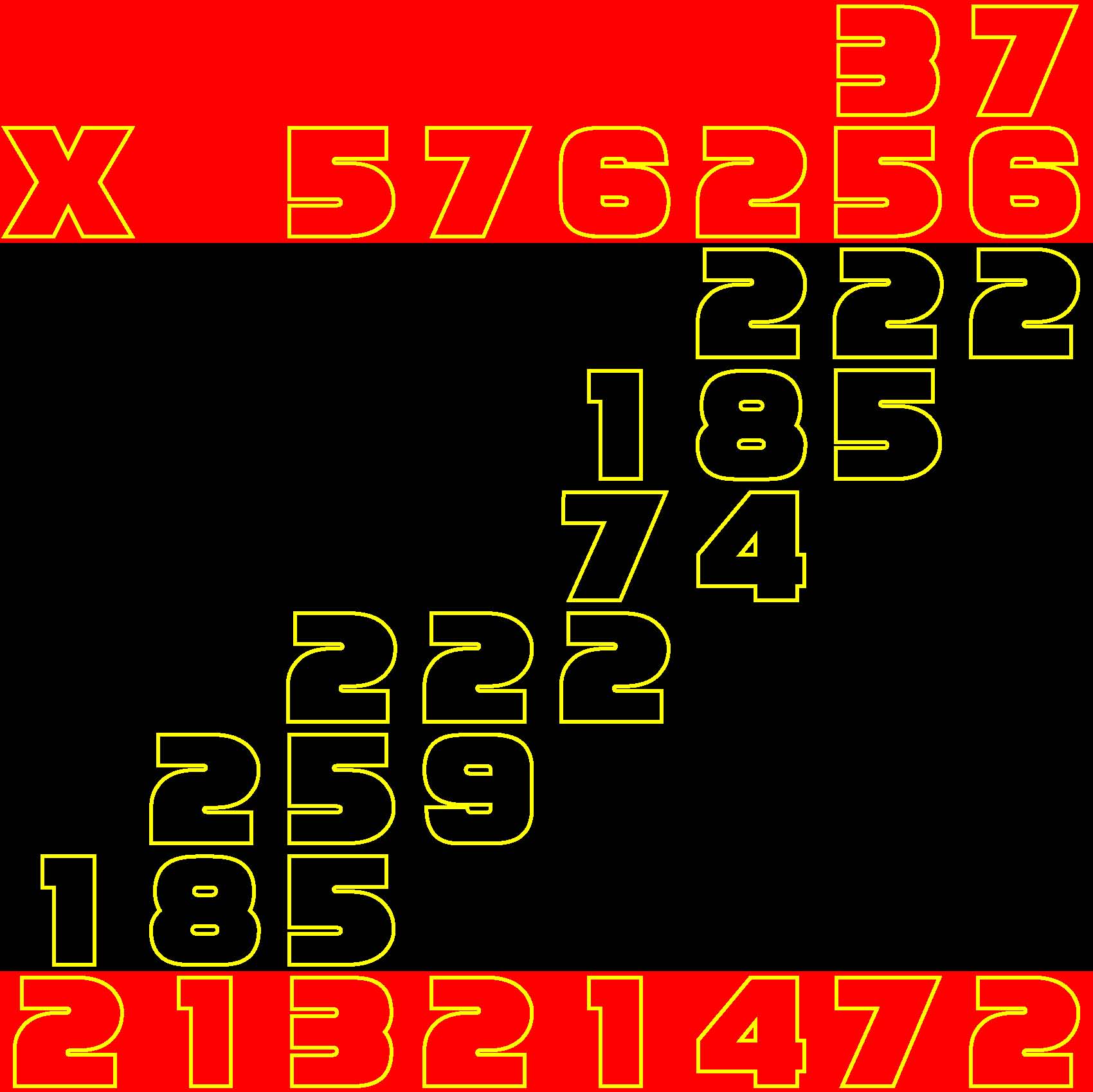
|

|

|

|

|

|

|
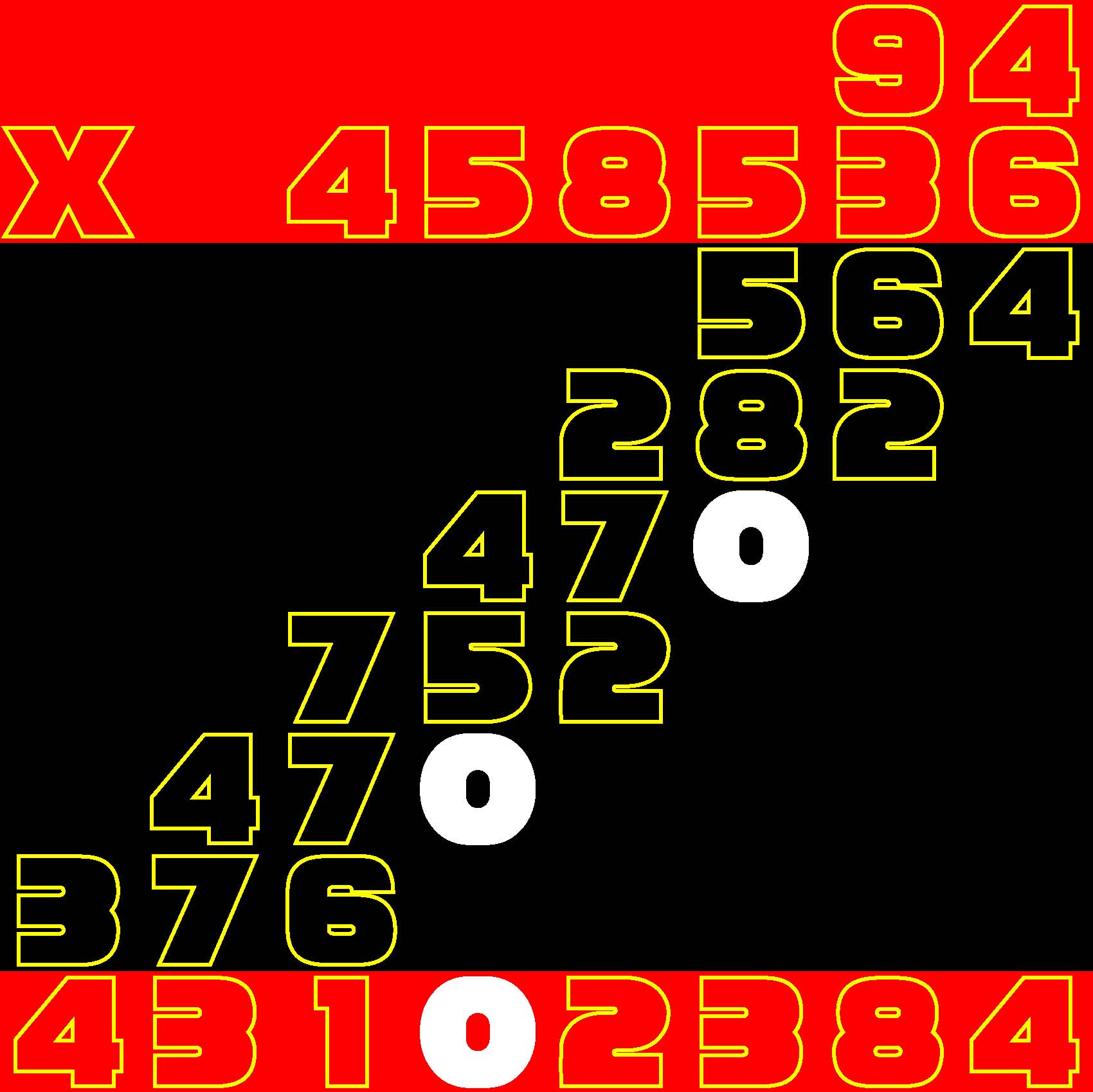
|
Beyond Anagrams
Words, Anagrams, Alphabetized Anagrams, Palettes, and the Alphabet by Francis Gurtowski
|
This is yet another serious, serious series of books created by Francis Gurtowski.
The prolific author is an authentic, ancient coder, going all the way back to IBM Poughkeepsie (Building 705, no less, second floor) and the heyday of OS/360, Robert Rex Seeber Jr. and the horizontal-microcoded System/360 Model 50, coding pads and the coding-pad veto, punch cards and keypunch machines, and self-modifying code. Francis Gurtowski is also a self-styled Henry Ford of contemporary, do-it-yourself, print-on-demand, book publishing. Henry Ford is synonymous with the assembly line, a perfected process for swiftly turning out a series of ingenious, finished products in a foolproof, mechanically-efficient manner. The way (or ways) in which a word is routinely spelled out (in the proverbial dictionary) is pretty much cut-and-dried. The notable exceptions being the annoying British variants. Such as analogue versus analog, and razzamatazz versus razzmatazz. It could be worse, I guess. If the Francophile Thomas Jefferson had had his way, way back when, then the United States of America would have adopted Anglo-Saxon as our official language. |
An anagram is an arbitrary transposition of an authoritative spelling (of a word) for the purpose of ambiguation.
From here on out, by "word" I shall mean a correct spelling of a word. By "anagram" I shall mean a permuted spelling. By "palette" I shall mean a spelling shorn of duplicate instances of letters. Brevity is a virtue. The twenty-six letters of the alphabet are the ultimate palette, but I know of no such word employing at least one instance of each. The longest palettes I could find are fourteen letters in length:
abcehlmorstuxy abceilmnorstuy abdeilmorstuxy acdefhilmnortu For example, bcehilmnoprsty is the palette of this threesome: comprehensibility incomprehensibility intercomprehensibility Palettes are as far beyond anagrams as anagrams are beyond words. |
Permit me to bastardize a bit of the jargon of relational database.
A First Normal Form of a word is the word itself. Such as caterer. A Second Normal Form of a word is the alphabetized anagrammatization of the word. Such as aceerrt. A Third Normal Form of a word is the alphabetized permutation of the word (and thus of its anagrams) shorn of duplicate instances of letters. Such as acert. Each First is subordinate to one and only one Second and to one and only one Third. Each Second is subordinate to one and only one Third. On the other hand, each Third subsumes one or more Seconds. Such as acert subsumes aacertt, aacerttt, acceert, aceeerrt, aceeertt, aceerrt, aceert, acerrt, acerrtt and acert itself. Each Second subsumes one or more Firsts. Such as aceerrt subsumes caterer, retrace and terrace. |
|

|
|
Anagrams Plus ... by Francis Gurtowski
|
This is yet another serious, serious series of books created by Francis Gurtowski.
The prolific author is an authentic, ancient coder, going all the way back to IBM Poughkeepsie (Building 705, no less, second floor) and the heyday of OS/360, Robert Rex Seeber Jr. and the horizontal-microcoded System/360 Model 50, coding pads and the coding-pad veto, punch cards and keypunch machines, and self-modifying code. Francis Gurtowski is also a self-styled Henry Ford of contemporary, do-it-yourself, print-on-demand, book publishing. Henry Ford is synonymous with the assembly line, a perfected process for swiftly turning out a series of ingenious, finished products in a foolproof, mechanically-efficient manner. |
This series of self-described, self-help books is more than just a collection of collections of word puzzles, in the English language.
It is a fun and effective way to progressively assimilate the entire vocabulary of the English language, at your own pace, one word-length at a time, five-letter words (and phrases) on up. The author obsessively digested dozens of English dictionaries into massive lists of words, arranged each of the respective lists into alphabetical order, and then scrambled the spellings multiple times. Each book is dedicated to a single length of word, with thousands and thousands of puzzles up front, and the solutions in the back of each book. The solutions are in alphabetical order, which gives away the fact that the solutions to the first anagrams begin with the first letter of the alphabet and the solutions to the last anagrams begin with the last letter of the alphabet. Moreover, one anagram is solved on each page, which practically gives away the solutions to the anagrams immediately before it and immediately after it. It always seemed odd to me that schools do not teach all the one-letter words first, all the two-letter words second, all the three-letter words third, and so forth. It is worth a try. |

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Hello, world.
A Terse Computer Program in a Strange Languageerase and type are the once familiar MS-DOS commands; dial, punch, and myEDSAC.exe are this author/coder/user's own MS-Win32 Console Applications; and tape.txt, boot.txt, and print.txt are Text Documents in MS-DOS format:
Then and NowThe limited lens of a rinky-dink oscilloscope variously rigged up to EDSAC once characterized the now denigrated Dark Ages of computer operations.Today, the display-type subcommands (such as general) of myEDSAC.exe are the mainstay of a bonus, debugging/code-optimization bundle:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Dot NotationA decimal shorthand for longhand binary numbers.
dial.c
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
boot.txt
octal.txt
decimal.txt
punch.c
tape.txt
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Cellular StoresAmerican-made ENIAC was deep-rooted in IBM tabulating equipment. ENIAC leveraged the prime medium of eighty-column, 960-hole, IBM cards to the hilt for both data input and data output.On the other hand, British-made EDSAC made do with the hangover of the sub prime medium of five-hole tape. Even so, EDSAC did so only for the input of both data and directives, not for the output of anything. Without tape output, EDSAC was at best merely half a Turing Machine. Cambridge University flaunted the uniquely British aesthetic of jerry-building, cobbled together radar accessories and a Creed Model 7B teleprinter, and mustered not one, but two, false-fronted bulk cellular stores. EDSAC's off-the-shelf acoustical delay lines had originated during the war for the purpose of motion detection in the context of radar pings. Boot storage consisted of 738 binary digits marshaled into forty-one eighteen-bit cells numbered 0-40. The larger of the British tandem of bulk cellular stores, general storage, was composed of 9,216 bits arranged into 512 cells of the same size and shape, and similarly numbered 0-511.
A fluffy cloud of formless storage capacity (which, after all, is what an acoustical delay line amounts to) is totally useless as a playing surface without a crisp time-sliced veneer of structure. Post-ENIAC computers require a proper digital game board for their dualistic code which consists of both data and directives where a binary number can play either role or both. An optical illusion of a honeycomb or an egg crate is far more satisfactory than the semblance of a blob. Unit cells of the former are numbered 0, 1, 2 and so on, discerning one cell from another cell is child's play, and the Lego-like parts conveniently snap together into pairs, quads, et cetera. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Lesson LearnedHardware test cases were slipped into EDSAC via a makeshift backdoor. It was a defining moment and an historic occasion when Cambridge University eventually bolted down the temporary scaffolding and dedicated it to the bootstrap.Herein the cells of boot storage are rechristened ranks, lest there be even more confusion differentiating them versus the cells of general storage. A total of 246 octal dials (six per rank) directly manipulated the boot store. However, the resulting lineup of data/directives was merely warehoused there because the bootstrap itself had to be replicated in general storage before the starter substance was appropriately sited for execution. A certain push button copied ranks 0-40 into cells 0-40 of general storage, and then another dashboard control pulled the trigger and (ready or not) got the entire computational caboodle chugging along down the track. Boot storage was strictly off-limits to the personnel who coded EDSAC; to every last one of the coders. Cambridge University strategically fenced off the boot store in favor of an absolute mystification seemingly bestowed fully formed by the gods. This benefaction loaded code concoctions from tape into general storage, and the bootstrap had it all: the bootstrap was the beneficiary of direct manipulation, it was sited at cell 0, and it was also entered there. However, those perogatives had consequences inasmuch as they prohibited the coders from ever again directly dialing code in by hand elegantly in octal. Intern/designated coder of the bootstrap, David J. Wheeler, alone had been afforded that privilege, and even him only once. After that, everyone had to program EDSAC at arm's length; in base-32, yet. Eighteen bits is not a multiple of five bits, and this affront to the worship of elegance chafed the more sensitive coders. Aesthetics aside, it was much too much to expect repetitions of the feat of 246 flawless dial settings. As a last resort, draconian measures encapsulated the bootstrap, and (as an added bonus) the primitive permanent arrangement also survived electrical power outages. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
EncapsulationThe prescribed use of the medium of tape for the input data was a no-brainer.However, the accompanying proposal to also use tape for the code itself faced a wall of skepticism despite the pitch/spiel that the envisioned canonical tape snippets of dependable data/directives would be equivalent to generic jigsaw puzzle pieces. Tape facilitated (a) encapsulation of modules of code besides the bootstrap, (b) infallible replication of the modules by machine for backup, and (c) immediate repair of the modules with the equivalent of errata slips. The equivalent of Band-Aids simply overlaid one datum/directive with another, while the likes of surgical repairs digressed to and from ad hoc curative subroutines sited in set-aside patch areas. Best-of-class subroutines were punched into separate tapes which were not only color coded. They were also labeled, archived, advertised, and retrieved from the vault on demand, and enterprising coders got a leg up by tapping into these predigested encapsulations. The personnel who operated EDSAC stood off and entered the spotlight as needed. Human beings on call at all times dismounted the current tape, mounted the next tape, pressed a button to resume the blocked code, and retreated offstage again. When a package was sufficiently proven, then and only then was the bundle turned over to a designated closer (someone analogous to a motion picture film editor) who proceeded to merge the constituent tapes into an ostensibly seamless stand-alone tape. Each directive (as well as each datum disguised as an directive) spanned a minimum of two rows of tape. Furthermore, the cryptic protocol for delineating these patterns further obfuscated the arm's-length coding rigmarole. The bootstrap took up its own store and squatted in the prime cells of general storage: the monolithic bootstrap was lodged at a fixed location in the general store while the various combinations of homeless modules in cahoots were indiscriminately domiciled just about anywhere. The convenient sophism of imagining the floaters layering the bootstrap deferred the inevitable reckoning with respect to occupancy.
Such superfluities were the gist of metaprogramming which was concerned with the superficialities of the code; not with the essential logic of the code itself. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Tear Down the WallAll of boot storage is now accessible to me, thanks to myEDSAC.exe.Moreover, myEDSAC.exe supports as many ranks of boot storage as it does cells of general storage. The simple-enough transformation from a niggling 41 ranks of boot storage
to a full-blown 2048 ranks of them
encourages an intimate unmediated machine language relationship with the zeros and ones of myEDSAC.exe channeling EDSAC. Bletchley Park and Jurassic ParkA stiff price for supple IBM cards far exceeded the shoe-laces-and-chewing-gum budgets of post-war Europe; on the other hand, limp tape was dirt cheap. The data processing medium of last resort was as ubiquitous as toilet paper because the cryptanalysts at Bletchley Park had militarized paper tape, of all things.Boffins (upon their return to academia and industry) reclaimed the familiar spools of long strips as narrow as ribbon. Furthermore, a sufficiency of hoarded rolls of blank tape had been squirreled away to result in a sharp spot-market devaluation, and a surplus stash at Cambridge University was put to especially good use. Over the course of its career, the workhorse of a service bureau for scientific applications chugalugged tape and spewed out printouts around the clock. However, in spite of its demonstrated prowess, EDSAC was unceremoniously scrapped after a curtailed lifetime of nonstop operation. The official narrative is that the one-off was shortsightedly melted down and the slag was sold off by the ton, but, instead, EDSAC may have been conveniently done away with ahead of an embarrassing pending collapse of the module library under its own administrative weight. Published verses of some of the extinct laboratory instrument's software miraculously survived the conflagration, and David J. Wheeler's densely encoded and almost double helical algorithm stands out as a Rosetta stone and a paradigm of a teaching aid. While its controversial code mutations amount to thought crimes (from the point of view of the computer programming nannies — who freak out at the mere thought of self-modifying code), David J. Wheeler's bootstrap — having been preserved in proverbial amber — is now even more opportune as a ritual to verify that myEDSAC.exe does not misrepresent the prospective coder's view of EDSAC. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Soul of a New MachineNo one knew enough yet to take David J.Wheeler aside and inform him that his mission was impossible. Young and gullible David J. Wheeler managed to configure the soul of the new machine even though the uniselectors were so scant in number besides so positively antique.As American historian Professor Jonathan Steinberg put it so well in a different context: "He had a sureness of touch and depth of insight into the tangled lines of force ... which led him to success after success. He made the impossible look easy, which is the indelible mark of the champion at any game." American essayist & poet Ralph Waldo Emerson would have classified David J. Wheeler as among the relatively great: "They are such, in whom, at the moment of success, a quality is ripe which is then in request. Other days will demand other qualities ..." David J. Wheeler carefully crafted the maximum of forty-one data/directives
separated each string of eighteen bits into six substrings of three bits apiece
converted the 246 binary triplets to base-8
and hand-dialed the octal numerals into the primitive read-only memory. The token amount of makeshift boot storage was the best that David J. Wheeler's academic advisor, Maurice V. Wilkes, could do on short notice. Fortunately, the niche itself was perfectly situated well out of reach. The nook was fortuitously tucked away where David J. Wheeler's precocious contribution to the business at hand (and what turned out to be David J. Wheeler's priceless bequest to all posterity) would not be fodder for hackers.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
RegistersBesides the boot store and the general store, EDSAC also had six even lower capacity information repositories known as its registers:
The accumulator register was the length of four cells. It consisted of a pad bit, a sign bit, and seventy bits of precision.
All negative numbers were expressed in twos-complement form. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
The dual use register — which was used (a) for both of the explicit multiplication operations and (b) for conjunction — was only two cells in length.
Half the length of the accumulator register.
The dual use register consisted of another bit of padding, another sign bit, and just thirty-four bits of precision.
It bears repeating that all negative numbers were expressed in twos-complement form. EDSAC's instruction format reserves eleven bits for an address — even though EDSAC itself did not make use of all of them. EDSAC never configured more than 512 cells of general storage. Inasmuch as 512 is 2^9, this accessory was nominally nine bits long.
myEDSAC.exe, on the other hand, implements a full complement of 2048 cells of general storage. Therefore my simulated pointer register is eleven bits long.
The directive register was one cell in length. Half the length of the dual use register. This accessory held the working copy of the cell selected by the pointer register for interrogation.
The input register and the separate output register were each five bits long.
The input register was the row of tape under the reading head. A read directive was supposed to incorporate the current row and then automatically advance the next row. However, if the tape was missing in action — as was often the case — then the read directive stalled. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Each row of tape had five punch sites.
More about the output register can be found ahead. A hole found punched into the tape was normally construed as a one and a null as a zero. No surprise there. However, the first punch site of each row was interpreted vice versa.
Consequently a blank row of tape was read as a sixteen rather than a zero. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Blinking LightsConspicuous panels of flashing lights — some positioned front and center, close at hand, at a spacious desk-like console — and others off to the side and literally wall-papering the whole room — which was accordingly reminiscent of a beloved Horn & Hardart Automat — became the darling icon for IBM computers.









It least they did once Thomas J. Watson, Sr. unabashedly pimped Robert Rex Seeber Jr.'s concept of a digital computer (SSEC, short for IBM Selective Sequence Automatic Calculator) in the show window of IBM headquarters in mid-Manhattan within easy walking distance from Times Square.
 The SSEC was visible to pedestrians on the sidewalk, and inspired a generation of cartoonists to portray the computer as a series of wall-sized panels covered with lights, meters, dials, switches, and spinning rolls of magnetic tape. The viral meme really burst into bloom when the off-Broadway sidewalk spectacle was portrayed on a front cover of The New Yorker.
 Thomas J. Watson, Sr., gave all-comers carte blanche to his triumph of market research disguised as customer education.
 While the heightened incandescence was superior salesmanship, for sure, as a practical matter, the light show also facilitated the operation of the IBM computer in the window.
 Moreover, throngs of bug-eyed onlookers extending onto 59th Street observed the binary contents of the plethora of registers et al change in real time. The SSEC ran at this location from January 1948 to July 1952, when it was replaced by the first-off-the line 701, IBM's first "mass"-produced computer (i.e, more than one). In retrospect, EDSAC missed the boat regarding blinking lights — unless you count the relatively infinitesimal dots and naughts on the tiny screens of strap-on, add-on cathode ray tubes. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Two Printer ModesThere was more to printing than what appeared on the printout because Letter Mode and Figure Mode were mutually exclusive. Computer programs had to toggle the mode of the printer in order to stay on message.The personnel who operated EDSAC were indoctrinated to press CLEAR before pressing GO. The bootstrap was entered at cell 0 only because the act of clearing EDSAC affected the pointer register. However, while that was a legitimate axiom, the computer program could not assume anything about the printer — because clearing EDSAC did not affect the output register. Nor did clearing EDSAC affect the mode of the printer. Thirty-two printer codes require a virtual sixth bit to distinguish ten decimal figures, twenty-six letters of the alphabet, sixteen punctuation marks, and six printer controls:
Spaces edited leading zeros, Carriage Return and Line Feed in tandem arrangement completed a line of printout, and, ultimately, it was essential to remember to flush the output register. A printer code was embedded in the cell that was found at the address that was embedded in the print directive itself. A selfie print directive ultimately performed the Carriage Return operation. Every alphanumeric, punctuation and control item except flush made a stopover in the single-item-wide output register on the way to the printer. Every item except flush was inoperative until it reached the printer. The last pending item remained on hold for so long as it remained buffered in the output register. A print directive delivered the holdover before buffering the next item. Hello again, world.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||